34. Дивергенция. Работа сил электрического поля. Потенциал. Градиент потенциала. Поверхности уровня.
Дивергенция
По определению дивергенцией
векторного поля
называется:
101\* MERGEFORMAT (.)
дивергенция вектора есть величина, инвариантная по отношению к преобразованию координат.
Вычислим дивергенцию вектора электрической индукции, пользуясь теоремой Гаусса:
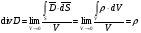202\* MERGEFORMAT (.)
Это означает, что истоками вектора электрической индукции являются свободные заряды с объёмной плотностью ρ.
Выразим вектор электрической индукции из формулы (1.10) и подставим в последнюю формулу:
,
отсюда:
303\* MERGEFORMAT (.)
Последняя формула означает, что истоками вектора напряжённости электрического поля являются не только свободные заряды с объёмной плотностью ρ, но и связанные заряды с объёмной плотностью:
404\* MERGEFORMAT (.)
Получим выражение для дивергенции вектора в декартовых координатах. Пусть точка наблюдения a находится внутри бесконечно малого параллелепипеда с гранями, параллельными координатным плоскостям (рис. 9). Вследствие бесконечной малости параллелепипеда интеграл от вектора электрической индукции по поверхности сводится к сумме шести потоков через шесть его граней.
Поток через грань 1 равен
,
где
есть проекция вектора
на ось x в точке x,
определяющей положение грани 1. Аналогично,
поток через грань 2 равен
,
где
есть такая же проекция вектора
на ось x в точке x-dx,
определяющей положение грани 2. Знак
минус учитывает, что направление
вектор-площадки или направления внешней
нормали к грани 2 противоположно
направлению оси x.
Рис. 9. К расчёту дивергенции вектора в декартовых координатах.
С учётом бесконечной малости параллелепипеда, общий поток через грани 1 и 2 равен:
.
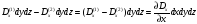Аналогичные выражения получаются для потоков через грани, перпендикулярные другим осям.
Поток вектора через замкнутую поверхность бесконечно малого параллелепипеда равен:
.
Тогда, согласно определению дивергенции (1.14), получим:
505\* MERGEFORMAT (.)
Работа сил электрического поля. Потенциал.
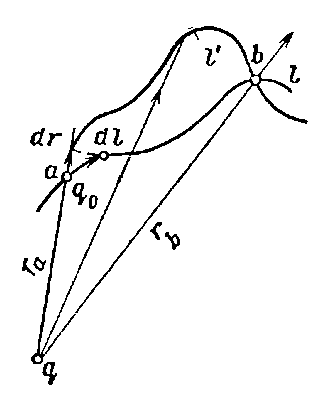
Рис. 10. К расчёту работы электрического поля.
Пусть в поле точечного заряда q перемещается по некоторой кривой l заряд q0 (рис. 10). На заряд q0 действует сила:
.
Работа по перемещению заряда q0 на отрезке dl равна:
,
где dr -
проекция отрезка dl
на направление
.
Работа при перемещении заряда q0
из точки a в точку b
равна:
606\* MERGEFORMAT (.)
Из полученного выражения вытекает важнейшее свойство электрического поля: работа сил электрического поля не зависимо от формы пути: согласно (1.19) работа зависит от начальной и конечной точки. Этот вывод, полученный для поля точечного заряда, легко обобщается на произвольное поле.
Консервативные силы: силы, работа которых не зависит от формы пути. Работа консервативной силы по замкнутому контуру равна нулю. Это – следствие закона сохранения энергии.
Потенциалом, или потенциальной функцией называется такая функция, разность значений которой в двух произвольных точках a и b равна работе сил электрического поля при переносе единицы электрического заряда из точки a в точку b.
707\* MERGEFORMAT (.)
Потенциал определяется с точностью до константы, которая определяется произвольно. Часто за нулевой потенциал принимается потенциал земли.
Градиент потенциала. Поверхности уровня.
Электрическое поле является векторным полем напряжённости и электрической индукции, а также скалярным полем потенциала. Поверхности равного потенциала – непрерывная поверхность, называется эквипотенциальной поверхностью, или поверхностью уровня. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю, следовательно, эквипотенциальная поверхность во всех точках перпендикулярна силовым линиям.
Градиент скалярной величины (в частности, потенциала) есть вектор, направленный по нормали к поверхности уровня (эквипотенциальной поверхности) и численно равный изменению потенциала в данной точке поля на единицу перемещения вдоль этой нормали. Положительное направление нормали – в сторону возрастания потенциала. При таком определении градиент потенциала имеет вид:
, 808\* MERGEFORMAT (.)
где
- орт (единичный вектор) вдоль нормали.
Рассмотрим производные по нормали дU/дn и по произвольному направлению l дU/дl (рис. 11), приращения Δn и Δl связаны соотношением:
,
отсюда вытекает соотношение между производными:
. 909\* MERGEFORMAT (.)
Из (1.22) видно, что производная по направлению l имеет максимальное значение, когда направление l совпадает с нормалью n.
Градиент скалярного поля есть вектор, величина и направление которого имеют величину и направление наискорейшего возрастания скалярного поля.
Согласно (1.21) проекции градиента на координатные оси равны:
С другой стороны, согласно (1.22):
Таким образом:
10010\* MERGEFORMAT (.)
В декартовых координатах градиент имеет вид:
. 11011\* MERGEFORMAT (.)
Рис. 11. К определению градиента потенциала.
Проекция градиента на произвольное направление равна производной по этому направлению:
. 12012\* MERGEFORMAT (.)
Из (1.20) следует, что напряжённость электрического поля равна градиенту электрического потенциала, взятому с обратным знаком:
. 13013\* MERGEFORMAT (.)