
3. Разработка математической модели объекта управления
Для построения замкнутой системы необходимо получить еематематическую модель в виде передаточной функции.
Для получения математической модели объекта управления, необходимой для синтеза автоматической системы регулирования и анализа ее работы, чаще всего используют активный метод и в ходе эксперимента снимают переходную характеристику, подавая на вход объекта ступенчатое воздействие. Проведя эксперимент и обработав его результаты, строят математическую модель объекта управления в виде передаточной функции, при этом видом передаточной функции задаются.
Экспериментальная переходная характеристика приведена на рисунке 3.1.
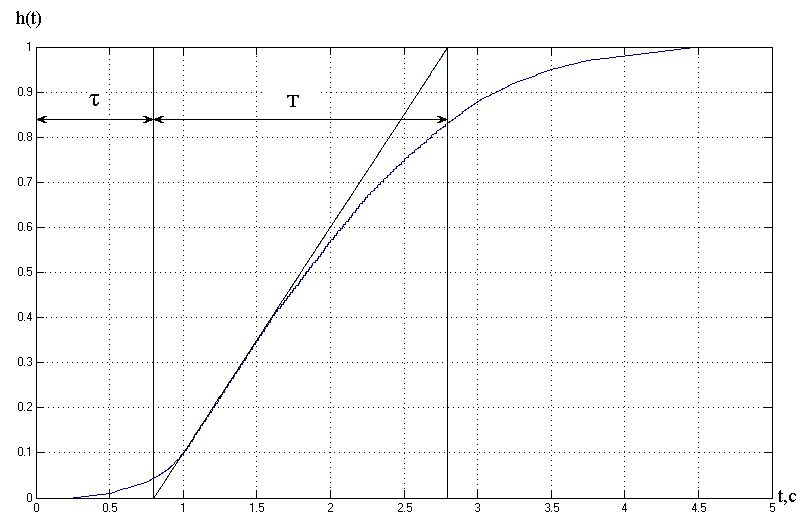
Рисунок 3.1 – Экспериментальная переходная характеристика
объекта управления.
Как видно из рисунка 3.1 переходная характеристика объекта обладает самовыравниванием и некоторым запаздыванием, поэтому в качестве исходной структуры математической модели объекта управления принимаем передаточную функцию вида:
![]() .
(3.1)
.
(3.1)
Для выбора исходных значений коэффициентов Коб, τ, Т, n используем методику приведенню в [1]. Из рисунка 2 Т=2 c ;τ=0.8;Коб=1; n примем равным 2.
Требования к точности математической модели сводятся к совпадению экспериментальной переходной характеристики с полученной переходной характеристикой объекта в трех точках: в начале координат, в точке перегиба и в установившемся режиме, а также совпадение первой производной переходной функции объекта и аппроксимирующей кривой в точке перегиба [1].
Постоянная времени Т=0.4 с. выбрана таким образом, чтобы выполнялись выше перечисленные требования. Коэффициент усиления объекта Коб равен единице.
В этом случае переходная функция объекта примет вид:
![]()
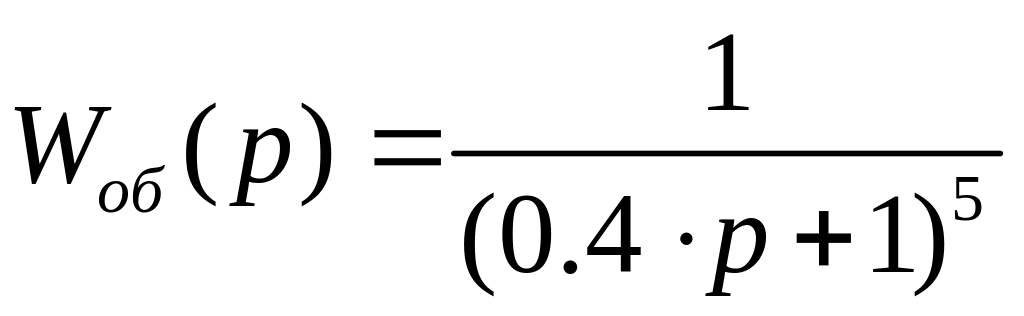 .
(3.2)
.
(3.2)
Для проверки точности аппроксимации, на ЭВМ, построена переходная характеристика по передаточной функции (3.2). Вид аппроксимирующей характеристики предложен на рисунке 3.2.
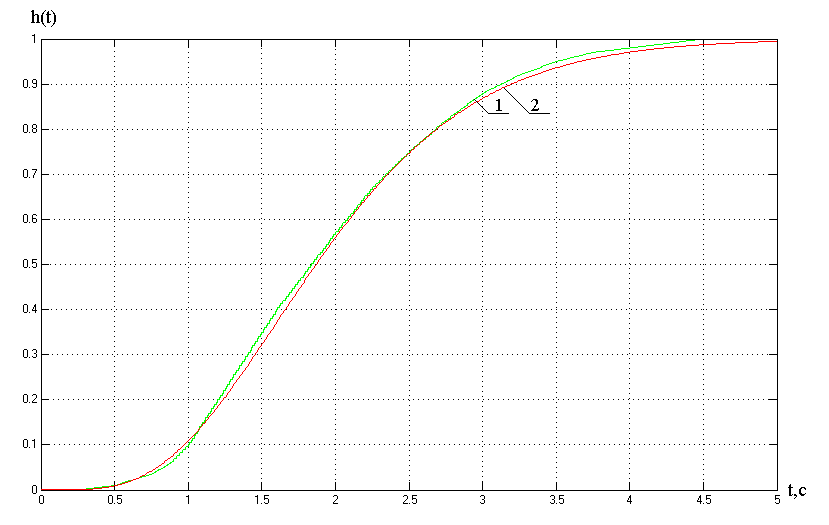
Рисунок 3.2 - Переходные характеристики объекта.
1-исходная характеристика объекта; 2-аппроксимирующая характеристика объекта.
Аппроксимирующая характеристика удовлетворяет изложенным выше критериям. Следовательно, точность аппроксимации удовлетворительна и передаточная функция (3.2) будет использована при синтезе автоматической системы регулирования.
4.Выьор критериев оптимальности и закона управления.
Качество функционирования любой автоматической системы управления существенно зависит от выбора критериев оптимальности и закона управления.
Автоматические системы регулирования, являясь замкнутыми динамическими системами с обратными связями, могут при неправильном выборе алгоритма функционирования регулятора или при неправильном выборе его параметров настройки потерять устойчивость. При определении оптимальных параметров настройки из условия минимума среднеквадратичной ошибки такое явление не наблюдается, однако как показывает опыт, переходные процессы в такой системе имеют характер затухающих колебаний, интенсивность затухания которых, как правило, оказывается явно недостаточной для того, чтобы систему можно было признать пригодной к эксплуатации.
Поэтому в критерий оптимального функционирования системы регулирования приходится обычно вводить дополнительные ограничения, с помощью которых можно целенаправленно влиять на возникающие в ней переходные процессы. Введение таких ограничений производится либо путем соответствующего усложнения показателя оптимальности (в этом случае минимизируется не просто значение среднеквадратичной ошибки, а
более сложная функция ошибки), либо при неизменном минимизируемом функционале в критерий оптимальности вводятся добавочные ограничения на показатели, характеризующие затухание переходного процесса. Первый способ удобен тем, что позволяет оставить неизменной процедуру поиска оптимума, лишь в той или иной степени усложнив ее. Однако при его практическом использовании возникают определенные затруднения в формулировке критерия оптимальности в каждом конкретном случае. Поэтому при практических расчетах предпочтение отдают второму способу ввода ограничений на затухание переходных процессов.
Практически наиболее удобными способами введения ограничений могут считаться следующие:
задание в плоскости корней характеристического уравнения системы области, за пределы которой не должен заходить ни один из этих корней;
задание в плоскости частотной характеристики разомкнутой системы регулирования области, включающей в себя «опасную» точку (-1,Ј0), внутрь которой не должна заходить эта характеристика.
Использование первого метода сопряжено с вычислением расширенных частотных характеристик объекта и регулятора.
В соответствии с критерием Найквиста динамическая система, устойчивая в разомкнутом состоянии, после замыкания ее обратной связью становится неустойчивой, если частотная характеристика этой системы в разомкнутом состоянии W(Јώ) охватывает точку с координатами (-1,Ј0) . Можно поэтому считать, что переходные процессы в системе имеют тем большее затухание, чем на большем удалении от указанной «опасной» точки располагается частотная характеристика разомкнутой системы.
Передаточная функция замкнутой системы имеет вид:
![]()
Следовательно
![]() (4.1)
(4.1)
Обозначим
![]() (4.2)
(4.2)
Использование
интегральной составляющей от ошибки
приводит к тому, что при частотная
характеристика регулятора при
![]() стремится к бесконечности. Поэтому
частотная
характеристика разомкнутой системы
при
также
уходит в бесконечность, а отношение
(4.2) стремится
к единице. С ростом частоты отношение
(4.1)
становится
отличным от единицы и в пределе при
стремится к бесконечности. Поэтому
частотная
характеристика разомкнутой системы
при
также
уходит в бесконечность, а отношение
(4.2) стремится
к единице. С ростом частоты отношение
(4.1)
становится
отличным от единицы и в пределе при
![]() стремится
к нулю (так как W(j
стремится
к нулю (так как W(j![]() )
стремится
к нулю.
Однако характер изменения
этого отношения при изменении
может быть различным в зависимости от
степени удаления характеристики
разомкнутой системы от точки (—1; j0).
)
стремится
к нулю.
Однако характер изменения
этого отношения при изменении
может быть различным в зависимости от
степени удаления характеристики
разомкнутой системы от точки (—1; j0).
Если характеристика W(j ) располагается достаточно далеко от точки
(—1; j0), то это отношение с ростом частоты монотонно уменьшается от единицы до нуля. Если же характеристика W(j ) проходит сравнительно близко к точке (—1; j0), то в некотором диапазоне частот 0< < Рез отношение не убывает, а наоборот, возрастает и только при > Рез начинает уменьшаться. Таким образом, при достаточно близком расположении частотной характеристики разомкнутой системы W(j ) к «опасной» точке (—1; j0) модуль частотной характеристики замкнутой системы Ф(j ) приобретает резонансный пик при некоторой резонансной частоте Рез. Чем ближе проходит характеристика W(j ) от точки (—1; j0), тем большим оказывается ордината этого пика. В пределе, когда характеристика W(j ) проходит через точку (—1; j0) и, следовательно, замкнутая система находится на границе устойчивости, резонансный пик характеристики замкнутой системы
|Ф (j Рез) | становится бесконечно большим.
Из сказанного следует, что величина резонансного пика модуля частотной характеристики замкнутой системы |Ф (j Рез) | может служить практически удобной мерой запаса устойчивости системы регулирования.
Из соотношения (4.1) можно установить, какие ограничения на расположение амплитудно-фазовой характеристики разомкнутой системы W(j ) накладывает ограничение на величину резонансного пика Ф (j Рез) .
Таким образом, параметры настройки регулятора могут считаться оптимальными, если среднеквадратичная ошибка регулирования достигает минимального значения при дополнительном условии, что показатель колебательности системы не превышает заданной величины М < M доп.
Кроме того при эксплуатации систем управления требуется чтобы в установившихся режимах в замкнутой системе отсутствовала статическая ошибка, что достигается путем введения астатизма в состав разомкнутой системы [2].
Исходя из этого в промышленных системах для управления объектами с самовыравниванием используются ПИ – регуляторы, а для управления объектами без самовыравниванием используются П – регуляторы.
Как видно из рисунков 3.1 и 3.2 объект относится к классу объектов с самовыравниванием поэтому в системе управления необходимо использовать ПИ – регулятор.
