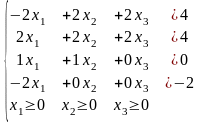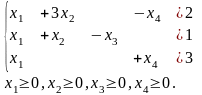Лабораторная работа № 2 метод больших штрафов

Задание: используя метод больших штрафов и симплексный алгоритм, найти экстремум целевой функции при заданных ограничениях.

Таблица 2

Варианты заданий

№ вар.	Целевая функция	Ограничения	Тип экстрем.
1			max
2			max

Продолжение табл.2
№ вар.	Целевая функция	Ограничения	Тип экстрем.
3			max
4			min
5			max
6			min
7			min
8			max

Продолжение табл.2
№ вар.	Целевая функция	Ограничения	Тип экстрем.
9			min
10			min
11			min
12			max
13			min
14			min
Окончание табл.2
№ вар.	Целевая функция	Ограничения	Тип экстрем.
15			min
16			min
17			max
18			max
19			min
20			max

Ход работы

1. Записать математическую модель задачи.

2. Записать математическую модель задачи в канонической форме.

3. Записать математическую модель задачи с учетом искусственных переменных.

4. Загрузить приложение Лин_прогр.exe.

5. Ввести в программу исходные данные и, используя симплексный метод, получить решение задачи. Сформировать файл отчета.

6. Открыть файл отчета c помощью программы Microsoft Excel, оформить и распечатать файл отчета.

7. Записать решение задачи

Содержание отчета

1. Текст задания.

2. Математическая модель задачи.

3. Математическая модель задачи в канонической форме.

4. Математическая модель задачи с искусственными переменными (с преобразованиями).

5. Симплекс-таблица решения задачи.

6. Результаты решения задачи.

7. Проверка выполнения условий-ограничений задачи для найденного решения.

Вопросы для подготовки

1. Когда в условия-ограничения вводятся искусственные переменные (формируется искусственный базис)?

2. Поясните необходимость ввода искусственных переменных в выражение целевой функции?

3. Какой коэффициент соответствует искусственной переменной в выражении целевой функции?

4. Почему искусственные переменные исключаются из выражения целевой функции расширенной ЗЛП?

5. Как определить с помощью решения расширенной задачи, что условия исходной задачи несовместны?

6. Когда исходная задача имеет более двух альтернативных решений (бесконечное множество решений), как это определить с помощью решения расширенной задач?

7. Когда исходная задача имеет единственное решение, как это определить с помощью решения расширенной задач?

8. Когда решение исходной задачи не ограничено, как это определить с помощью решения расширенной задач?