29. Расчёт переходных процессов операторным методом. Свойства преобразования Лапласа, изображение производных и интегралов.
РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ОПЕРАТОРНЫМ МЕТОДОМ –
с помощью преобразования Лапласа.
Определения.
Оригиналом называется функция переменной t (времени), имеющая следующие свойства:
1. f(t)=0, если t<0;
2.
;
3. функция f(t) удовлетворяет условиям Дирихле, т.е. на каждом конечном интервале она имеет конечное число максимумов и минимумов и разрывов первого рода.
Сопоставим ей функцию комплексной переменной p=+j, задаваемую формулой (1):
, (1)
функция F(p) называется изображением по Лапласу функции f(t).
Если функция f(t)
удовлетворяет вышеперечисленным
условиям, то интеграл (1) абсолютно
сходится в области Rep=>0
(т.е. сходится интеграл
).
В этой области функция F(p)
является аналитической функцией
комплексного аргумента, т.е. в каждой
точке она разлагается в степенной ряд.
Обозначения изображения по Лапласу:
, F(p)=L[f(t)], 
.
Обратное преобразование Лапласа:
, (2)
обозначение:
L-1[F(p)]=f(t), 
Основные свойства прямого преобразования Лапласа.
1. Свойство линейности: если
Fk(p)=L[fk(t)],
то:
, (3)
где ak - числа.
Т.е. изображение линейной комбинации оригиналов есть линейная комбинация изображений.
2. Теорема запаздывания.
. (4)
3. Теорема смещения.
, (5)
где: - положительная или отрицательная постоянная.
4. Умножение изображений: изображение свертки оригиналов равно произведению изображений:
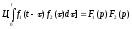(6)
5. Предельные соотношения:
если
,
то
, (7)
если
,
то
, (8)
6. Изображение производной
L[f(t)]=pF(p)-f(0+), (9)
где f(0+) значение функции в начальный момент времени.
Изображение n-й производной имеет вид:
L[f(n)(t)]=pnF(p)-pn-1f(0+)-pn-2f(0+)-…-f(n-1)(0+). (10)
В частном случае, при нулевых начальных условиях:
L[f(t)]=pF(p), (11)
L[f(n)(t)]=pnF(p). (12)
7. Изображение интеграла
.