Вопросы к экзамену+ответы(шпоры). Р-РС-ЭП 2 курс, 2 семестр Рябов Н.И. / Ответы / 33.0

33. Поле заряженного круглого цилиндра. Поле двух бесконечно тонких линейных проводов.

Поле заряженного круглого цилиндра.

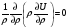
У поверхности цилиндра (ρ=a, σ - поверхностная плотность заряда):

Вводя погонную плотность заряда τ=2πσa, получим:

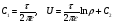
Поле двух бесконечно тонких линейных проводов

Провода имеют конечные погонные плотности заряда τ и -τ. Потенциал в любой точке пространства есть сумма потенциалов обоих проводов:

Уравнение эквипотенциали (k ‑ параметр):

Возведя в квадрат и преобразовав, получим:

Прибавив к левой и правой части (l(1+k²)/(1-k²))², получим уравнение:

Это ‑ уравнение окружности с центром в точке (x₀,y₀) и радиусом r₀:

.

Из геометрии известно, что произведение отрезков секущей, проведённой из некоторой внешней точки к окружности равно квадрату отрезка касательной к этой окружности, проведённой из этой же точки.

Рассмотрим окружность, проходящую через источники поля (провода). Ось x - её секущая, произведение отрезков секущей от центра эквипотенциальной линии до проводов [x₀,2], [x₀,1] равно:

следовательно, радиус эквипотенциальной линии является отрезком касательной к рассматриваемой окружности, т.е эта окружность ортогональна к эквипотенциальной линии.

Вывод: окружности, проходящие через источники поля (провода), являются силовыми линями.

Поле заряженного круглого цилиндра. (Из лекции)

Используя теорему Гаусса, рассчитаем поле заряженного цилиндра. Пусть бесконечный цилиндр радиуса a равномерно заряжен электричеством с поверхностной плотностью σ. Определим напряжённость поля в точке, отстоящей от оси цилиндра на расстояние ρ. Проведём через точку наблюдения цилиндрическую поверхность S₀ высотой h и дополним её до замкнутой поверхности плоскостями S₁ и S₂ (рис. 7).

Рис. 7. К расчёту поля заряженного цилиндра. Рис. 8. Поле заряженного цилиндра.

Вследствие симметрии вектор электрической индукции направлен перпендикулярно к боковой поверхности S₀ и одинаков во всех её точках. Таким образом, поток через площадки S₁ и S₂ равен нулю, и в соответствии с равенством Гаусса – Остроградского имеем: .

Заряд Σq внутри поверхности S, распределён на цилиндре радиуса a с высотой h и равен: .

Отсюда:

Поле внутри заряженного цилиндра равно нулю.

На рис. 8 показаны графики зависимости векторов электрической индукции и напряжённости от расстояния до оси цилиндра. При переходе через заряженную поверхность цилиндра вектор электрической индукции изменяется скачком на σ.