28. Расчёт переходных процессов операторным методом. Представление сопротивлений, индуктивностей и ёмкостей. Представление независимых источников.
РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ОПЕРАТОРНЫМ МЕТОДОМ –
с помощью преобразования Лапласа.
Определения.
Оригиналом называется функция переменной t (времени), имеющая следующие свойства:
1. f(t)=0, если t<0;
2.
;
3. функция f(t) удовлетворяет условиям Дирихле, т.е. на каждом конечном интервале она имеет конечное число максимумов и минимумов и разрывов первого рода.
Сопоставим ей функцию комплексной переменной p=+j, задаваемую формулой (1):
, (1)
функция F(p) называется изображением по Лапласу функции f(t).
Если функция f(t) удовлетворяет
вышеперечисленным условиям, то интеграл
(1) абсолютно сходится в области Rep=>0
(т.е. сходится интеграл
).
В этой области функция F(p) является
аналитической функцией комплексного
аргумента, т.е. в каждой точке она
разлагается в степенной ряд.
Обозначения изображения по Лапласу:
, F(p)=L[f(t)], 
.
Обратное преобразование Лапласа:
, (2)
обозначение:
L-1[F(p)]=f(t), 
Уравнения электрических цепей в операторной форме.
1. Резистор.
U(p)=RI(p), I(p)=U(p)/R=gU(p), (25)
где:
U(p)
u(t), I(p)
i(t),
т.о. операторное сопротивление резистора совпадает с его сопротивлением.
2. Индуктивность. Основное уравнение индуктивности имеет вид:
,
т.к.
,
то:
. (26)
Эквивалентные схемы индуктивности показаны на рис. 2.
Рис. 2. Эквивалентные схемы индуктивности.
3. Емкость. Основное уравнение емкости имеет вид:
,
т.к.
,
то:
. (27)
Эквивалентные схемы емкости показаны на рис. 3.
Рис. 3. Эквивалентные схемы емкости.
4. Источники ЭДС и тока, вообще говоря, зависящие от времени, представляются такими же источниками, номиналы которых равны изображениям по Лапласу функций исходных источников:
e(t)
E(p), J(t)
J(p).
В частности:
e(t)=E1(t)
E/p
Пример 1.
Рис. 4. R-C цепь
Разложим UC(p) на элементарные дроби методом неопределенных коэффициентов:
,
отсюда:
,
следовательно:
,
E, 
,
следовательно:
.
Пусть в схеме рис. 4 стоит синусоидальный источник: e(t)=Esin(t), его изображение имеет вид: E(p)=E/(p2+2).
Тогда:
Разложим UC(p) на элементарные дроби методом неопределенных коэффициентов:
,
отсюда:
,
следовательно:
,
,
,
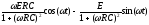следовательно:
.
Таким образом, в расчете операторным методом сразу получается и свободная составляющая – экспонента и принужденная составляющая – синусоида.