Вопросы к экзамену+ответы(шпоры). Р-РС-ЭП 2 курс, 2 семестр Рябов Н.И. / Ответы / 9.0

9. Теорема об активном двухполюснике, условие передачи в нагрузку максимальной мощности.

ПРИНЦИП ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА

Очень важным принципом эквивалентности, широко применяемым при анализе линейных электрических цепей, является принцип эквивалентного генератора (теорема об активном двухполюснике, или теорема Гельмгольца — Тевенена). Он формулируется следующим образом: любая линейная электрическая цепь, рассматриваемая относительно двух выводов (активный двухполюсник), эквивалентна реальному источнику с ЭДС, равной напряжению между этими выводами при размыкании внешнего участка цепи, подключенного к этим выводам (режим холостого хода), и внутренним сопротивлением, равным входному сопротивлению пассивного двухполюсника, получающегося при равенстве нулю всех ЭДС для источников ЭДС и токов для источников тока рассматриваемого двухполюсника. Применимость этого принципа к любой линейной электрической цепи доказывается на основании принципов компенсации и наложения.

Пусть в электрической цепи выделен активный двухполюсник и ветвь с сопротивлением r (рис. 5.14, а), которое может быть и изменяющимся. Применив принцип компенсации, получим эквивалентную схему (рис. 5.14,6), для которой

Е=U=rI. (5.19)

Теперь применим принцип наложения и составим две схемы с двумя частными режимами: в первой из них (рис. 5.14, в) действуют только источники внутри активного двухполюсника, а ЭДС, полученная по принципу компенсации, полагается равной нулю, а во второй (рис. 5.14, г) действует только ЭДС компенсации (5.19), а двухполюсник считается пассивным. Его входное сопротивление r_ВХ.

Ток в ветви с сопротивлением r по принципу наложения равен сумме частичных токов I=I'+I"=I_К-U/r_ВХ, т. е. U=r_ВХ(I_К-I), I=I_K-rI/r_ВХ, I(r_ВХ+r)/r_ВХ=I_K.

В частности, в режиме холостого хода I=0 и U=U_Х=r_ВХI_К. Следовательно,

U=U_Х-r_ВХI=rI. (5.20)

Последнее уравнение соответствует эквивалентной схеме, показанной на рис. 5.14, д с ЭДС Е_ЭК=U_Х, выражающей сформулированный выше принцип. Согласно (5.20) ток

I=Е_ЭК/(r_ВХ+r)=U_Х/(r_ВХ+r). (5.21)

Если источник ЭДС преобразовать в источник тока, то схема эквивалентного генератора получится такой, как на рис. 5.14, е. Вольт-амперная или внешняя характеристика эквивалентного генератора по рис. 5.14, д или е показана на рис. 5.14, ж.

Следует заметить, что обе схемы эквивалентного генератора применимы только для расчета токов и напряжений в участке цепи, подключенном к рассматриваемому активному двухполюснику. Для мощностей, развиваемых источниками, и мощностей потерь внутри активного двухполюсника схемы замещения, полученные на основании принципа эквивалентного генератора, неадекватны.

Применение принципа эквивалентного генератора позволяет упростить решение многих задач, и поэтому его применение иногда относят к методам расчета, хотя он и носит более общий характер.

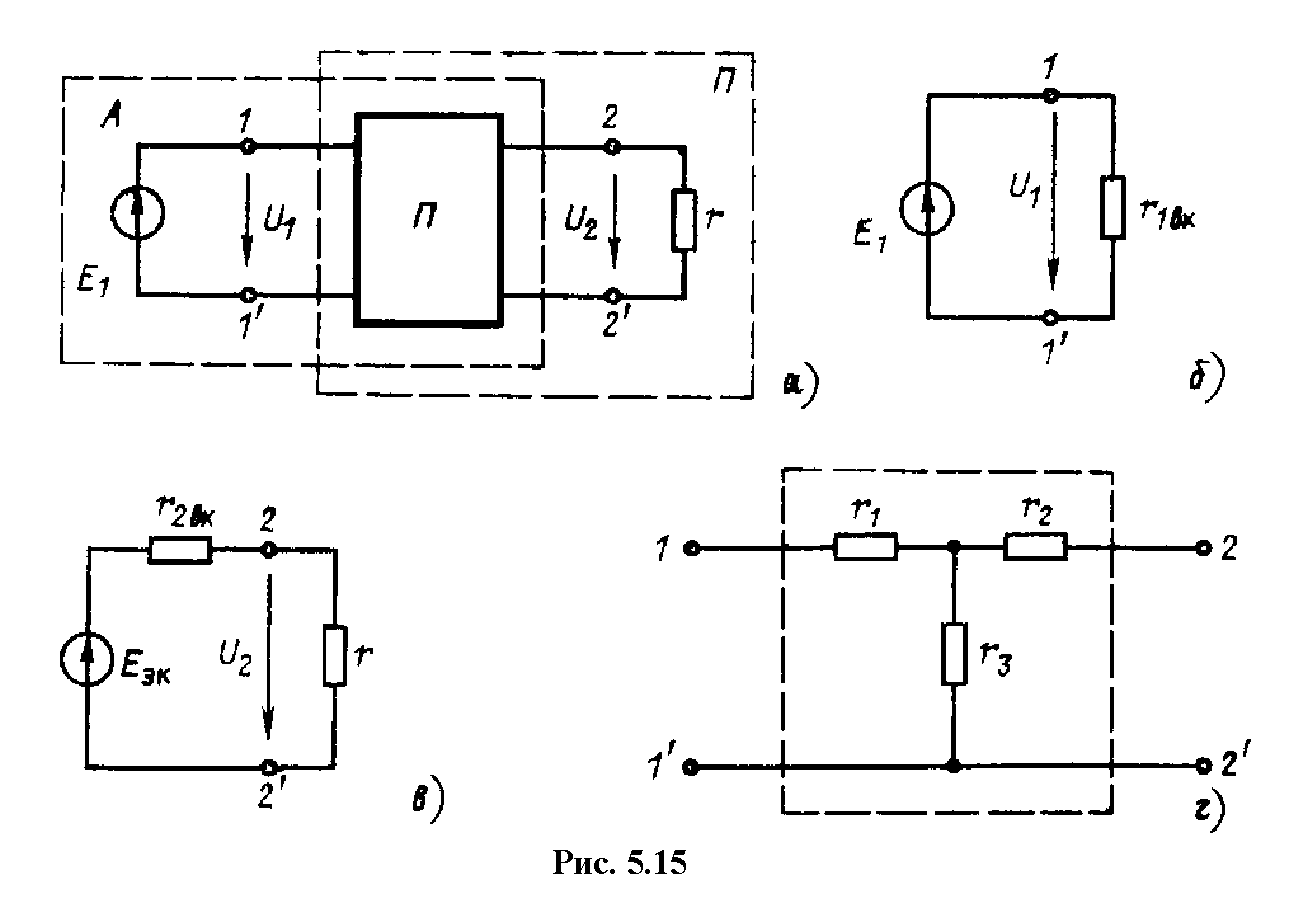
Применение принципа эквивалентного генератора весьма удобно при рассмотрении пассивного четырехполюсника, к одной паре выводов которого подключен источник ЭДС Е₁, а к другой паре выводов — приемник с сопротивлением r (рис. 5.15, а). Такую схему со стороны выводов 1-1 можно рассматривать как пассивный двухполюсник с сопротивлением r_1ВХ (рис. 5.15,6), а со стороны выводов 2-2' - как активный двухполюсник с входным сопротивлением r_2ВХ и э.д.с. Е_ЭК (рис. 5.15, в).

Если, например, пассивный четырехполюсник имеет схему, показанную на рис. 5.15, г, то параметры эквивалентной схемы

r_1ВХ=r₁+r₃(r+r₂)/(r₃+r₂+r); r_2ВХ=r₂+r₁r₃/(r₁+r₃); Е_ЭК=Е₁r₃/(r₁+r₃)

Представление четырехполюсника в виде эквивалентной схемы, изображенной на рис. 5.15, в, применяется при рассмотрении электронных схем. Для приемника с сопротивлениями r схемы рис. 5.15, а и в полностью эквивалентны. Однако если рассчитать мощность пассивного четырехполюсника (в сопротивлениях r₁ r₂ и r₃) и мощность потерь в эквивалентной схеме (сопротивление r_2ВХ), то эти мощности могут оказаться равными только в редких частных случаях.

Интересно сопоставить принцип эквивалентного генератора с принципом компенсации. И тот и другой дают возможность представить двухполюсник в виде эквивалентного источника, однако принцип компенсации приводит к идеальному источнику ЭДС (без внутреннего сопротивления), а принцип эквивалентного генератора — к реальному источнику (с внутренним сопротивлением r_ВХ). ЭДС источника, полученного на основании принципа компенсации, зависит от тока, а параметры источника, полученного на основании принципа эквивалентного генератора, не зависят от режима работы подключенного к активному двухполюснику участка цепи. Принцип компенсации применим как к линейным, так и к нелинейным цепям. Принцип эквивалентного генератора применим только к линейным цепям.

Пример. По принципу эквивалентного генератора найти выражение для тока I₀ в ветви с измерительным прибором (рис. 5.16, д), если ток источника тока J=10 мА, сопротивление r=100 Ом, сопротивление измерительного прибора. r₀=50 Ом, а сопротивления r₁ двух противоположных плеч моста изменяются одновременно от нуля до 2r; построить график изменения тока I₀ в зависимости от сопротивления r₁.

Решение. Разомкнем ветвь с измерительным прибором (рис. 5.16,б), отключив прибор, и найдем токи I_1Х=I_2Х=J/2.

Напряжение U_Х (рис. 5.16,6) определим из уравнения r₁J/2+U_Х-rJ/2=0, откуда U_Х=(r‑r₁)J/2.

Входное сопротивление двухполюсника относительно выводов ветви с измерительным прибором (рис. 5.16, в) r_ВХ=(r‑r₁)/2.

По принципу эквивалентного генератора (5.21)

I₀=U_Х/(r_ВХ+r₀)=J(r‑r₁)/(2r₀+r+r₁)

Подставляя численные значения, получим:

I₀=10(100-r₁)/(100+100+r₁)

На рис. 5.16, г показан график изменения тока I₀ в зависимости от сопротивления r₁. Из рисунка видно, что зависимость тока от сопротивления нелинейная (в отличие от линейных соотношений между ЭДС, напряжениями и токами при изменении сопротивления) и что при изменении сопротивления r₁ изменяется не только значение тока I₀, но и его направление.

ПЕРЕДАЧА ЭНЕРГИИ ОТ АКТИВНОГО ДВУХПОЛЮСНИКА К ПАССИВНОМУ

Для исследования передачи энергии от активного двухполюсника к пассивному вернемся к эквивалентной схеме, показанной на рис. 5.14, д, и будем считать, что r_ВХ — входное сопротивление активного двухполюсника (источника энергии) и Е_ЭК=U_Х — эквивалентная ЭДС остаются постоянными, а r — входное сопротивление пассивного двухполюсника может принимать любое значение.

Прежде всего установим соотношение между сопротивлениями r_ВХ и r, при выполнении которого мощность пассивного двухполюсника максимальна.

Мощность пассивного двухполюсника определяется выражениями

Р=Е_ЭКI-r_ВХI²=U_ХI-r_ВХI² (5.22)

Р=rI², (5.23)

где Е_ЭКI=U_ХI — мощность, развиваемая эквивалентным активным двухполюсником; r_ВХI² — мощность потерь в этом двухполюснике (в сопротивлении r_ВХ).

Для определения тока I, при котором мощность Р максимальна, найдем производную от Р по I из уравнения (5.22) и приравняем ее нулю:

dР/dI=U_Х-2r_ВХI=0,

откуда искомый ток I=U_Х/(2r_ВХ) [уравнением (5.23) пользоваться нельзя, так как его правая часть содержит две переменные: r и I].

В общем случае (рис. 5.14, д) ток I=U_Х/(r_ВХ+r). Значит, мощность максимальна при

r=r_ВХ, (2.24)

т. е. при равенстве входных сопротивлений пассивного и активного двухполюсников.

По (5.23) при r=r_ВХ мощность

P_МАКС=U_Х²/(4r_ВХ).

Отношение мощности Р пассивного двухполюсника к мощности Р_А=U_ХI, развиваемой эквивалентным активным двухполюсником, называется КПД эквивалентного активного двухполюсника:

. (5.25)

Из (5.25) следует, что при максимальной мощности пассивного двухполюсника КПД равен 0,5. Более высокие значения КПД будут при r>r_ВХ.

КПД реального активного двухполюсника равен КПД эквивалентного только при выполнении определенного условия. Если при отключении пассивного двухполюсника от реального активного в ветвях последнего не будет токов и потерь, так же как и в эквивалентной схеме на рис. 5.14, д, то КПД реального и эквивалентного активных двухполюсников равны. При невыполнении этого условия КПД реального активного двухполюсника меньше КПД эквивалентного двухполюсника.

Полученные результаты применим, например, для характеристики режима линии передачи электрической энергии небольшой длины, у которой утечкой тока (между проводами) можно пренебречь.

Если в начале линии передачи напряжение U₁ поддерживается неизменным (рис. 5.17, а), то линию можно представить в виде последовательного соединения активного двухполюсника с источником ЭДС Е_ЭК=U_Х=U₁ (без внутреннего сопротивления), резистивного элемента, учитывающего сопротивление проводов r_Л, и пассивного двухполюсника — приемника с сопротивлением r (рис. 5.17, а). По (5.22) и (5.25) найдем мощность Р₂ приемника и КПД линии передачи:

(2.26)

Мощность, развиваемая источником,

P₁=U₁I;

напряжение на выводах приемника

U₂=U₁-r_ЛI.

По полученным уравнениям на рис. 5.17,6 построены зависимости U₂, P₁ Р₂ и  от тока I, полностью характеризующие режим линии.

При r= (холостой ход линии) ток I=0 (на рис. 5.17, б — точка в начале координат), при r=r_Л ток определяется отрезком 0а и при r=0 (короткое замыкание линии) значение тока максимально и равно I_К. Кроме того, при r=r_Л мощность Р₁ определяемая отрезком ас, равна удвоенной мощности приемника (ас=2аb=2bc), и КПД =0,5.

Рис. 5.17

По эквивалентной схеме (рис. 5.17, а) установим еще связь между потерями в проводах линии (в сопротивлении r_Л) и мощностью приемника Р₂:

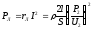, (2.27)

где l — длина линии; S — сечение каждого провода.

Из (2.27), в частности, следует, что при Р₂ =const с повышением напряжения U₂ требуется меньшее значение тока I и, следовательно, уменьшаются потери в проводах, что в свою очередь позволяет уменьшить сечение проводов. Конечно, при этом надо усилить изоляцию проводов линии.

В случае передачи по линии электрической энергии при большой мощности стремятся получить возможно больший КПД, для чего необходимо, как непосредственно следует из (5.26), иметь r_Л<<r. При передаче сигналов по линии связи стремятся получить максимальную мощность в приемнике, что приводит к низкому значению КПД.