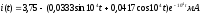Вопросы к экзамену+ответы(шпоры). Р-РС-ЭП 2 курс, 2 семестр Рябов Н.И. / Ответы / 22.0 23.0 24.0

22. Расчет переходных процессов классическим методом. Составление характеристического уравнения.

23. Расчет переходных процессов классическим методом. Независимые и зависимые начальные условия.

24. Расчет переходных процессов классическим методом. Корни характеристического уравнения. Характер переходного процесса.

ЭТАПЫ РАСЧЁТА ПЕРЕХОДНОГО ПРОЦЕССА КЛАССИЧЕСКИМ МЕТОДОМ. 1) Составление характеристического уравнения и поиск его корней. 2) Поиск принуждённой составляющей. 3) Нахождение независимых и зависимых начальных условий. 4) Вычисление констант свободной составляющей из начальных условий.

Решение получается в виде: ()

где - принуждённое решение, n – порядок ОДУ (число индуктивностей и ёмкостей) - корни характеристического уравнения, могут быть комплексными, - постоянные интегрирования, определяемые из граничных условий.

Формула () справедлива для случая различных вещественных корней характеристического уравнения.

Пусть характеристическое уравнение имеет n корней и , тогда

Если число одинаковых корней равно m, то соответствующий член имеет вид:

В линейных пассивных схемах (без управляемых источников) все действительные корни отрицательные.

Характеристическое уравнение – алгебраическое n-ой степени с действительными коэффициентами, если оно имеет комплексные корни, то они парные сопряжённые, а действительная часть меньше или равна нулю.

, тогда соответствующий член свободной составляющей принимает вид

Рассмотрим каждый из этапов расчёта. 1) Составление характеристического уравнения. Составляется по ОДУ заменой на , но само ОДУ выводить не обязательно

отличается от комплексного сопротивления ветви только тем, что заменяется на . Поэтому надо записать сопротивления индуктивностей в виде pL, сопротивления ёмкостей в виде 1/(pC) и составить систему уравнений по I и II законам Кирхгофа. Приравняв к нулю определитель этой системы уравнений, получим характеристическое уравнение. Можно составить систему уравнений по методу контурных токов или узловых потенциалов, приравняв определитель полученной системы к нулю, получим характеристическое уравнение. Корни получающихся уравнений одинаковы.

При составлении характеристического уравнения все источники из цепи должны быть выключены!

Ключ размыкается.

,

Свободная составляющая имеет вид:

Характеристическое уравнение схемы можно получить следующим образом. Из схемы выключаются все источники, потом берётся произвольная ветвь схемы, размыкается: получаются 2 зажима, относительно этих двух зажимов вычисляется входное сопротивление полученной схемы и приравнивается нулю, т.е. характеристическое уравнение примет вид:

. Это – метод входного сопротивления.

Пример:

Ключ замыкается:

Вычислим входное сопротивление относительно зажимов источника Е:

Свободная составляющая принимает вид

Третий способ получения характеристического уравнения: из схемы после коммутации выключаются все источники (ЭДС – закорачиваются, тока – разрываются), относительно двух произвольных узлов схемы вычисляется проводимость и приравнивается нулю:

Это – метод входной проводимости.

Пример:

Свободная составляющая имеет вид:

2) Поиск принуждённой составляющей. Расчёт установившегося режима после коммутации: если источник постоянный, делается расчёт цепи постоянного тока (емкость - разрыв, индуктивность – закорачивающий провод), если источник синусоидальный, режим рассчитывается методом комплексных амплитуд с последующим определением мгновенных значений по комплексным амплитудам. Для расчёта периодического несинусоидального сигнала используется разложение в ряд Фурье. Рассмотрим схему предыдущего примера:

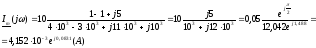
3) Вычисление независимых начальных условий. По схеме до коммутации определяются напряжения на ёмкостях и токи индуктивностей, которые не меняются в момент коммутации

Пример:

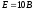
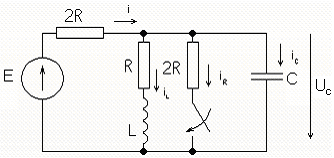
Расчёт независимых начальных условий. Эквивалентная схема:

Расчёт зависимых начальных условий. Эквивалентная схема для момента времени составляется следующим образом. В схеме после коммутации емкости заменяется источниками ЭДС с величиной ЭДС, равной U_C(0), а индуктивности – источниками тока с токами, равными I_L(0), по этой схеме рассчитываются все остальные токи и напряжения по законам Кирхгофа.

Из эквивалентной схемы:

I закон Кирхгофа для узла 1

(1)

Зная независимые начальные условия и , находим - зависимое начальное условие. По формуле (1) – найдём

(2) зная независимые условия, находим , по (2) - вычислим и 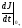(независимые источники).

Составим схему, где вместо независимых источников ЭДС и тока стоят источники и , вместо индуктивностей – источники тока , вместо емкостей - источники напряжения , по этой схеме вычисляем все производные: , ,

Из (1) и (2) следует: и , что позволяет вычислить вторые производные для всех токов и напряжений, и т.д.

Характеристическое уравнение и его корни:

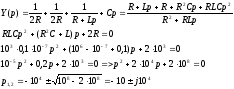
Свободная составляющая имеет вид:A, B – неопределённые постоянные.

Принужденная составляющая вычисляется по эквивалентной схеме установившегося режима после коммутации.

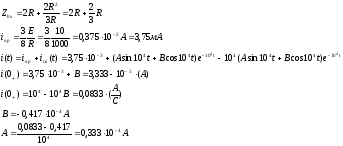
Ответ: