
Вопросы к экзамену+ответы(шпоры). Р-РС-ЭП 2 курс, 2 семестр Рябов Н.И. / Ответы / 24.0 25.0
.docx24. Расчет переходных процессов классическим методом. Корни характеристического уравнения. Характер переходного процесса.
25. Расчёт переходных процессов классическим методом. Дифференциальные уравнения, свободная и принуждённая составляющие.
Переходные
процессы в последовательном RLC-контуре
R,
L,
C;

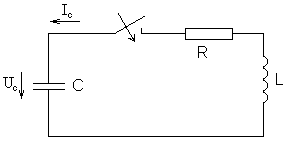
Характеристическое
уравнение
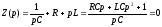

 (8)
(8)
независимые начальные условия


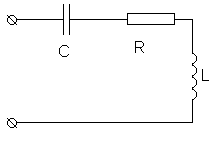
эквивалентная схема для момента 0+






Принужденная составляющая любой величины равна нулю (в схеме после коммутации нет источников питания ) т.е. переходный процесс состоит из одной свободной составляющей. В зависимости от знака подкоренного выражения в (8) свободная составляющая будет иметь различный вид.
 (9)
(9)
величина, определяемая формулой (9) называется критическим сопротивлением контура.
Если
 >
> ,то
корни характеристического уравнения,
определяемые формулой (8), действительные
различные и переходный процесс имеет
вид:
,то
корни характеристического уравнения,
определяемые формулой (8), действительные
различные и переходный процесс имеет
вид:

 <0
<0
Процесс имеет апериодический характер




 ,
, 
 (10)
(10)

 (см. алгебру)
(см. алгебру)

 (11)
(11)
 (12)
(12)
 ;
;

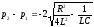
 >0,
>0,
 <0
<0
график


Если
 то корни действительные равные
то корни действительные равные

 -
максимум тока ( по модулю)
-
максимум тока ( по модулю)
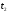 -
максимум
-
максимум
 и точка перегиба
и точка перегиба
 ,
ищется из условия
,
ищется из условия
 с ростом
с ростом
 падают
падают
 т.е. растет время перезарядки, с ростом
т.е. растет время перезарядки, с ростом
 то же.
то же.
Если
 ,
то корни характеристического уравнения
действительные равные
,
то корни характеристического уравнения
действительные равные
 тогда решение имеет вид
тогда решение имеет вид


 ;
;



отсюда
:
 (13)
(13) (14)
(14)
 (15)
кривые такие же по форме.
(15)
кривые такие же по форме.
Если R<RKP , то корни характеристического уравнения комплексные сопряженные.
Выведем
обозначения :
 ,
,
 (16)
(16)
Тогда
 (17)
(17)
где
 угловая
частота и
угловая
частота и
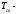 период свободных или собственных
колебаний контура,
период свободных или собственных
колебаний контура,
 коэффициент
затухания, корни характеристического
уравнения имеют вид:
коэффициент
затухания, корни характеристического
уравнения имеют вид:
 (18)
(18)
 (19)
(19)
 (20)
(20)





 ;
;
 ;
;


 ,
, 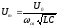 (20)
(20)






= (22)
(22)
 и
и
 - частота собственных колебаний и
коэффициент затухания , определяются
только параметрами R,
L,
C,
начальная фаза
- частота собственных колебаний и
коэффициент затухания , определяются
только параметрами R,
L,
C,
начальная фаза
 зависит только от них ,
зависит только от них , кроме параметров контура зависят также
от
кроме параметров контура зависят также
от


Быстрота затухания
характеризуется отношением напряжений
в момент времени
 и
и


Эта постоянная величина - от времени не зависит, а зависит только от R,L,C; она называется декремент колебания. Логарифмический декремент колебания:
 (23)
(23)
При малом декременте
процесс затухает медленно, с ростом R
растет декремент и период собственных
колебаний
 , когда
, когда
 ,
,
 ,
,

т.
е. процесс становится апериодическим
при
 ,
,
 ,
,

 ,
,

 ,
, 
 ,
, 
т. е. колебания происходят без затухания с резонансной частотой контура , энергия переходит из электрического поля емкости в магнитное поле индуктивности и обратно.
