Вопросы к экзамену+ответы(шпоры). Р-РС-ЭП 2 курс, 2 семестр Рябов Н.И. / Ответы / 32.0

32. Поток вектора индукции. Теорема Гаусса - Остроградского.

Поток вектора индукции. Теорема Гаусса – Остроградского.

Вектором – площадкой называется векор, направленный перпендикулярно площадке и численно равный её величине. Направление вектора связано с направлением обхода площадки правилом правого буравчика: если буравчик вращается по направлению обхода площадки, то буравчик движется по направлению вектора – площадки, или с конца вектора – площадки положительное направление обхода уидится направленным против часовой стрелки. В других случаях положительным считают направление, внешнее для заданной области и т.п.

Пусть имеется произвольная конечная поверхность. Разобьём её на бесконечно малые площадки и каждую из них зададим в виде вектора.

Потоком вектора через площадку называется произведение длин этих векторов на косинус угла между ними. Это – скалярное произведение двух векторов:

.

Физический смысл: если - скорость в потоке жидкости, то скалярное произведение - количество жидкости, протекающей через площадку в единицу времени.

Пусть имеется замкнутая поверхность произвольной формы, окружающая точечный заряд q. Поток вектора 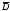через площадку равен:

101\* MERGEFORMAT (.)

Рис. 4. Поток вектора через элементарную площадку.

Рис. 5. К выводу равенства Гаусса – Остроградского.

Здесь dΩ – элементарный телесный угол, под которым видна площадка dS, рассматриваемая из точки расположения заряда, а совпадает по направлению с внешней нормалью к S. Заметим, что мерой телесного угла dΩ является отношение сферической поверхности dS₀ к квадрату её радиуса, причём .

Полный поток вектора через замкнутую поверхность равен:

В соответствии с (1.12) получаем

,

т.к. сумма телесных углов вокруг точки равна 4π.

Рис. 6. Заряд q находится вне объёма, ограниченного поверхностью S.

Если замкнутая поверхность S не содержит внутри себя заряд (рис. 6), то при обходе поверхности от точки А до точки Б по обращённой к заряду стороне поверхности значение телесного угла возрастает, а затем при движении от Б к А по противоположной заряду стороне поверхности уменьшается и по возращению в точку А телесный угол становится равным нулю.

Пусть в объёме, ограниченной поверхностью S, имеется множество точечных зарядов q₁, q₂, …, q_n. На основании принципа суперпозиции имеем:

,

где - векторы индукции созданные в рассматриваемой точке зарядами q₁, q₂, …, q_n. Поэтому поток вектора индукции через поверхность S равен:

.

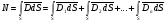Но в соответствии с полученным ранее результатом, слагаемые равны q₁, q₂, …, q_n. Таким образом:

202\* MERGEFORMAT (.)

Это – равенство Остроградского – Гаусса: поток вектора индукции через произвольную замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри объёма, ограниченного этой поверхностью.

Используя теорему Гаусса, рассчитаем поле заряженного цилиндра. Пусть бесконечный цилиндр радиуса a равномерно заряжен электричеством с поверхностной плотностью σ. Определим напряжённость поля в точке, отстоящей от оси цилиндра на расстояние ρ. Проведём через точку наблюдения цилиндрическую поверхность S₀ высотой h и дополним её до замкнутой поверхности плоскостями S₁ и S₂ (рис. 7).

Рис. 7. К расчёту поля заряженного цилиндра.

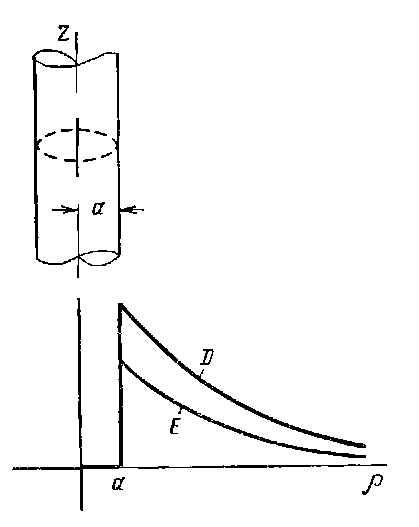
Рис. 8. Поле заряженного цилиндра.

Вследствие симметрии вектор электрической индукции направлен перпендикулярно к боковой поверхности S₀ и одинаков во всех её точках. Таким образом, поток через площадки S₁ и S₂ равен нулю, и в соответствии с равенством Гаусса – Остроградского имеем:

.

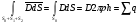Заряд Σq внутри поверхности S, распределён на цилиндре радиуса a с высотой h и равен:

.

Отсюда:

Поле внутри заряженного цилиндра равно нулю.

На рис. 8 показаны графики зависимости векторов электрической индукции и напряжённости от расстояния до оси цилиндра. При переходе через заряженную поверхность цилиндра вектор электрической индукции изменяется скачком на σ.