20. Активная, реактивная, полная мощность цепи, комплексная мощность, их взаимосвязь.
Рассмотрим энергетические соотношения в цепи синусоидального тока.
Положим, что за элементарный промежуток времени dt через поперечное сечение прохода в направлении, принятом за положительное для тока i (см. рис. 6.15), проходит электрический заряд dq. Перемещение заряда в направлении, совпадающем с положительным направлением ЭДС источника, сопровождается элементарной работой dA=edq источника. Такая электромагнитная энергия отдается источником во внешнюю цепь и затрачивается на работу dA=udq по перемещению заряда dq в положительном направлении напряжения и через пассивный двухполюсник.
Мгновенная мощность, производимая и отдаваемая источником ЭДС и получаемая двухполюсником, равна скорости совершения работы в данный момент времени:
p=dA/dt=ui.
Напряжение и ток на входе пассивного двухполюсника в общем случае сдвинуты по фазе на угол . Примем начальную фазу напряжения u=0 и найдем из (6.28) начальную фазу тока i=—. При таком условии мгновенные значения напряжения и тока
u=Umsint; i=Imsin(t‑).
Мгновенная мощность
.
(3.37)
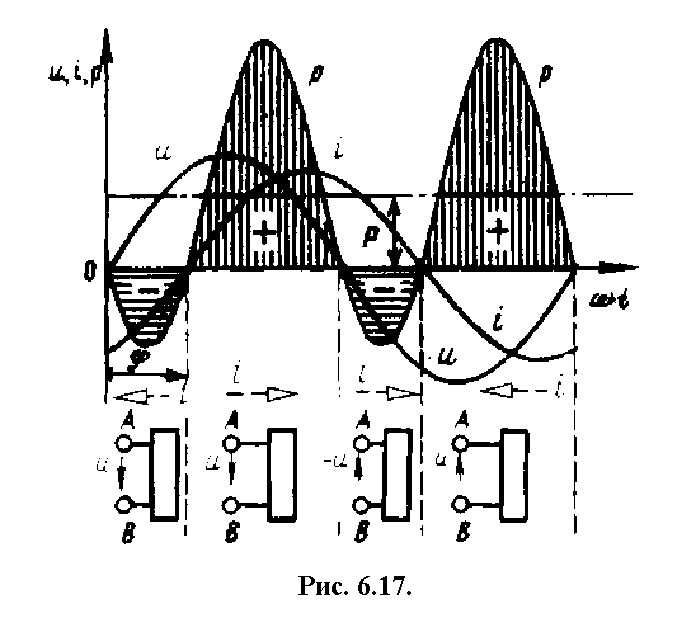
Мгновенная мощность имеет постоянную составляющую и гармоническую составляющую, частота которой в 2 раза больше частоты напряжения и тока (рис. 6.17). Мгновенная мощность, получаемая двухполюсником и отдаваемая источником напряжения (ЭДС), положительна, когда у напряжения и u тока i одинаковые знаки, т. е. когда действительные направления напряжения и тока в двухполюснике одинаковы и одинаковы действительные направления ЭДС и тока источника (см. рис. 6.15); она отрицательна, когда у напряжения и тока разные знаки, т. е. когда действительные направления напряжения и тока в двухполюснике противоположны и противоположны действительные направления ЭДС и тока источника.
Действительные направления и и I в течение отдельных интервалов времени показаны на рис. 6.17.
Когда мгновенная мощность отрицательна,
энергия поступает не в двухполюсник, а
возвращается из двухполюсника источнику
ЭДС. Такой возврат энергии источнику
питания возможен, так как энергия
периодически запасается в магнитных и
электрических полях элементов цепи,
входящих в состав двухполюсника. Энергия,
отдаваемая источником и поступающая в
двухполюсник в течение времени t,
равна
.
На графике она соответствует площади,
ограниченной кривой p
и осью абсцисс на интервале времени t.
Знаками плюс и минус отмечены заштрихованные
площади, соответствующие энергии,
поступающей в двухполюсник и возвращаемой
источнику.
Если двухполюсник состоит только из резистивных элементов, энергия накопляться в нем не может. В этом случае нет сдвига фаз между напряжением и током (=0). Знаки тока i и напряжения и в любой момент времени одинаковы и p0 (см. далее рис. 6.18, а), и нет таких моментов времени, когда энергия возвращалась бы из двухполюсника источнику питания.
|
|
|
|
|
Рис. 6.18 |
||
Среднее значение мгновенной мощности за период называется активной мощностью, или иногда просто мощностью, и, как следует из (6.37),
.
(6.38)
Активная мощность, получаемая пассивным двухполюсником, не может быть отрицательной (иначе двухполюсник не потреблял бы энергию, а генерировал ее), поэтому всегда cos0, т. е. на входе пассивного двухполюсника —/2<</2. Случай P=0, =|/2| теоретически возможен для двухполюсника, не имеющего резистивных элементов, а содержащего только индуктивные и емкостные.
Электрические машины и аппараты конструируют для работы при определенных значениях напряжения и тока. Поэтому их характеризуют не активной мощностью, зависящей от сдвига фаз между напряжением и током, а полной мощностью
S=UI, (6.39)
равной произведению действующих напряжения и тока.
Очевидно, что полная мощность равна наибольшему значению активной мощности при заданных напряжении и токе. Отметим также, что амплитуда гармонической составляющей мгновенной мощности (6.37) численно равна полной мощности. Размерность полной и активной мощностей одинаковая, однако единицу измерения мощности в применении к полной мощности называют вольт-ампер (ВА). Это позволяет при численном выражении полной мощности кратко говорить: мощность столько-то вольт-ампер, так как наименование единицы (вольт-ампер) сразу указывает, что речь идет о полной мощности.
Отношение активной мощности к полной, равное косинусу угла сдвига фаз между напряжением и током, называется коэффициентом мощности:
Р/S=UIcos/(UI)=cos. (6.40)
Для лучшего использования электрических машин и аппаратов желательно иметь возможно более высокий коэффициент мощности или возможно меньший сдвиг по фазе тока относительно напряжения, т. е. стремиться получить cos=1. Так, например, для питания приемника мощностью 10000 кВт при cos=0,7 источник питания должен быть рассчитан на мощность 14 300 кВА, а при cos=1 — на 10000 кВА.
Высокий коэффициент мощности желателен также для уменьшения потерь при передаче энергии по линиям. При данной активной мощности Р приемника ток в линии тем меньше, чем больше значение cos:
I=Р/(Ucos).
При расчетах электрических цепей находит применение так называемая реактивная мощность:
Q=UIsin. (6.41)
Она положительна при отстающем токе (>0) и отрицательна при опережающем токе (<0). Единицу мощности в применении к измерению реактивной мощности называют вар (название происходит от сокращения слов «вольт», «ампер» и «реактивный»). Это отдельное наименование позволяет говорить вместо реактивная мощность просто мощность, равная стольким-то вар.
Активная, реактивная и полная мощности связаны соотношениями
. (6.42)
Для увеличения коэффициента мощности (cos) приемника нужно, очевидно, уменьшать его реактивную мощность.
В то время как активная мощность определяет (в среднем) совершаемую работу или передаваемую энергию в единицу времени, полная и реактивная мощности не определяют ни совершаемой работы, ни передаваемой энергии за единицу времени. Однако в электроэнергетике по аналогии с понятием активной мощности приписывают реактивной мощности аналогичный смысл, а именно ее рассматривают как мощность отдачи, получения или передачи некоторой величины, которую, хотя она и не является энергией, условно называют реактивной энергией
WP=Qt
Размерность этой величины одинакова с размерностью энергии. Единицу измерения реактивной энергии называют вар-час; напомним, что энергия в электроэнергетике обычно измеряется в ватт-часах. Если наряду с энергией нужно рассматривать и реактивную энергию, то во избежание путаницы для внесения четкого различия этих двух понятий энергию называют активной.
На практике реактивная энергия, как и активная, измеряется счетчиками. При изменяющейся с течением времени нагрузке по показаниям счетчиком можно определить средний коэффициент мощности (cos)СР, предварительно вычислив
(tg)СР=WP/WA=QСРt/PСРt=QСР/PСР (6.43)
где WA — активная энергия; PСР и QСР — средние значения активной и реактивной мощностей.
Рассмотрим теперь простой прием, позволяющий найти активную и реактивную мощности при известных комплексных напряжении и токе. Он заключается в том, что нужно взять произведение комплексного напряжения U и комплекса I*, сопряженного с комплексным током I. Это произведение называют комплексной мощностью, которую обозначают S.
Пусть U=Uu, I=Ii, так что I*=I‑i; и S=UI*=UuI‑i=UIu‑i=UI= =UIcos+jUIsin, т. е.
S=UI*=Р+jQ. (6.44)
Отсюда видно, что действительная часть комплексной мощности равна активной мощности, а мнимая часть — реактивной. Модуль комплексной мощности равен полной мощности S.
Из приведенных выше основных выражений для мощностей S, S, Р и Q получается ряд других выражений, в которые входят параметры пассивного двухполюсника или активные и реактивные составляющие тока и напряжения:
S=UI*=ZII*=ZI2; S=UI*=UY*U*=Y*U2; S=UI=zI2=yU2;
P=UIcos=UaI=UIa=zI2cos=rI2=yU2cos=gU2;
Q=UIsin=zI2sin=xI2=yU2sin=bU2.
Для абсолютного значения реактивной мощности справедливы также выражения
|Q|=UpI=UIp.
Из равенств S=UI, Р=UaI=UIa и |Q|=UpI=UIp следует, что стороны треугольников напряжений и токов пропорциональны мощностям S, Р и |Q|. Подобный им треугольник, стороны которого в произвольно выбранном масштабе равны мощностям S, Р и |Q|, называется треугольником мощностей.