27. Расчёт переходных процессов операторным методом. Обратное преобразование Лапласа. Поиск оригинала по изображению.
РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ОПЕРАТОРНЫМ МЕТОДОМ –
с помощью преобразования Лапласа.
Определения.
Оригиналом называется функция переменной t (времени), имеющая следующие свойства:
1. f(t)=0, если t<0;
2.
;
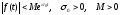3. функция f(t) удовлетворяет условиям Дирихле, т.е. на каждом конечном интервале она имеет конечное число максимумов и минимумов и разрывов первого рода.
Сопоставим ей функцию комплексной переменной p=+j, задаваемую формулой (1):
, (1)
функция F(p) называется изображением по Лапласу функции f(t).
Если функция f(t)
удовлетворяет вышеперечисленным
условиям, то интеграл (1) абсолютно
сходится в области Rep=>0
(т.е. сходится интеграл
).
В этой области функция F(p)
является аналитической функцией
комплексного аргумента, т.е. в каждой
точке она разлагается в степенной ряд.
Обозначения изображения по Лапласу:
, F(p)=L[f(t)], 
.
Обратное преобразование Лапласа:
, (2)
обозначение:
L-1[F(p)]=f(t), 
Основные свойства прямого преобразования Лапласа.
1. Свойство линейности: если
Fk(p)=L[fk(t)],
то:
, (3)
где ak - числа.
Т.е. изображение линейной комбинации оригиналов есть линейная комбинация изображений.
2. Теорема запаздывания.
. (4)
3. Теорема смещения.
, (5)
где: - положительная или отрицательная постоянная.
4. Умножение изображений: изображение свертки оригиналов равно произведению изображений:
(6)
5. Предельные соотношения:
если
,
то
, (7)
если
,
то
, (8)
6. Изображение производной
L[f(t)]=pF(p)-f(0+), (9)
где f(0+) значение функции в начальный момент времени.
Изображение n-й производной имеет вид:
L[f(n)(t)]=pnF(p)-pn-1f(0+)-pn-2f(0+)-…-f(n-1)(0+). (10)
В частном случае, при нулевых начальных условиях:
L[f(t)]=pF(p), (11)
L[f(n)(t)]=pnF(p). (12)
7. Изображение интеграла
. (13)
Изображение некоторых функций времени.
Определение 1. Единичная функция 1(t) имеет следующий вид:
, (14)
аналогично:
, (14)
тогда:
, (15)
Определение 2. Единичный импульс или -функция (t) имеет следующий вид:
, (16)
причем выполнено условие:
. (16)
Объяснить появление такой парадоксальной функции можно следующим образом: рассмотрим функцию в виде импульса конечной длительности (рис. 1,а).
,
легко видеть, что
и
.
Кроме этого, рассмотрим функцию e(t,) (рис. 1,б):
,
очевидно, что выполнены следующие соотношения:
,
.
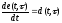Из этих соотношений следует, что:
. (16)
|
а) |
б) |
|
Рис. 1. d-функция (а) и e- функция (б). |
|
Отметим следующее важное свойство -функции:
, (17)
где t1 – некий фиксированный момент времени:
,
тогда:
отсюда:
Изображения
Пусть f(t)=1(t), тогда:
,
т.е.
L[1(t)]=1/p.
Пусть f(t)=(t), тогда:
Пусть f(t)=et, тогда:
,
т.е.
L[et]=1/(p-).
Другие функции.
L[t]=1/p2.
L[te-t]=1/(p+)2.
L[tn-1e-t/(n-1)!]=1/(p+)n.
L[sin(0t)]=0/(p2+02).
L[cos(0t)]=p/(p2+02).
…
Нахождение оригиналов по изображениям
Часто изображение имеет вид рациональной дроби:
, (18)
m<n, многочлены F1(p) и F2(p) не имеют общих корней, следовательно, дробь несократима, коэффициенты ak, bk – действительные.
Оригинал f(t) изображения (18) можно найти по формуле, называемой теоремой разложения:
. (19)
Это – сумма вычетов подынтегральной функции F(p)ept в обратном преобразовании Лапласа (2) относительно всех ее полюсов pk, здесь pk - простые корни характеристического уравнения
F2(p)=0, (20)
причем один из них может быть равным нулю,
F2(p)=dF2(p)/dp.
Поскольку коэффициенты знаменателя ak,– действительные числа, то комплексные корни уравнения (20) (если они есть) являются парными сопряженными. Известно, что функции с действительными коэффициентами от комплексных сопряженных значений независимого переменного – сами комплексные сопряженные, т.е. если pi и pi* комплексные сопряженные корни характеристического уравнения (2), то:
. (21)
Для полюсов произвольной кратности справедлива формула:
. (22)
Если:
и степень числителя меньше степени знаменателя, тогда F(p) разлагается на простые дроби:
, (23)
(23)
Оригинал каждой дроби в разложении (23) ищется с помощью таблиц, в результате получаем:
.