Приложение 2 Пример выполнения работы

Требуется разработать синхронную последовательную схему, которая должна детектировать последовательность 0110011, поступающую через единственный вход данных. Логическое значение на этом входе может меняться после каждого тактового импульса. Схема имеет один выход, состояние которого равно 1 только тогда, когда со входа целиком считана указанная последовательность. Решение следует провести двумя способами: используя модель Мура (D-триггера и булев базис) и модель Мили (JK-триггера и базис И-НЕ).

1-й способ. Используем модель Мура.

Как вам известно, из теоретической части курса, любой автомат можно задать с помощью графа, или с помощью таблиц переходов-выходов. В нашем примере будут приведены оба способа.

Граф автомата строится исходя из условия задачи. Как показано на рисунке 1, в рассматриваемом случае последовательность реализуется за восемь шагов, что предполагает наличие восьми состояний.

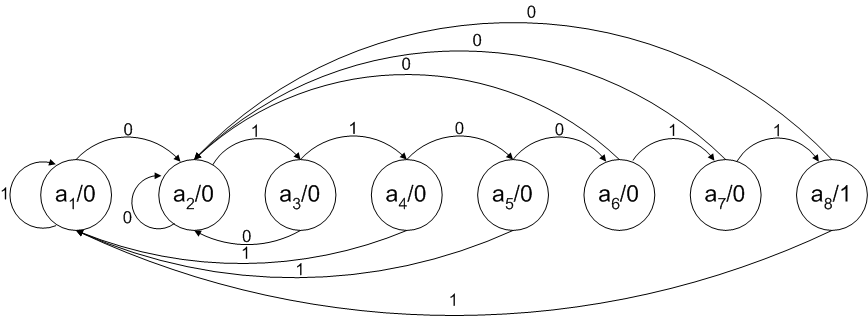
Рисунок 1. Граф автомата Мура

Начальным состоянием является состояние a₁, в котором на выходе присутствует значение 0. Схема изменяет свое состояние, если на входе появляется 0 (точнее, если логический 0 имеется на входе во вре­мя прихода тактового импульса). Это первый 0 последователь­ности, который требуется обнаружить, и при его появлении схема переходит в состояние a₂. При этом на выходе сохраняет­ся значение 0. Поступление следующих значений входной по­следовательности приводит к переходу схемы в состояния a₃, a₄, a₅, a₆, a₇ и, наконец, a₈. И только в последнем, восьмом состоя­нии, после приема последнего бита заданной последовательно­сти, на выходе схемы устанавливается значение 1. После этого следующая 1 возвращает схему в начальное состояние a₁. Если же принимается 0, то он может быть первым нулем но­вой последовательности, поэтому происходит переход в состоя­ние a₂. Все остальные переходы на графе автомата, имею­щие место до приема последнего бита последовательности, явля­ются либо переходами в состояние a₁, если принимается 1, либо – в состояние a₂, если принимается 0 (который рассматри­вается в качестве первого 0 последовательности). В целом, если в условии нет дополнительных ограничений, в качестве воз­можной последовательности необходимо рассматривать все ча­стные последовательности битов, которые могут появиться до приема последнего бита заданной последовательности.

Графу автомата на рисунке 1 соответствует следующая отмеченная таблица переходов автомата Мура:

Таблица 1. Отмеченная таблица переходов автомата Мура
	0	0	0	0	0	0	0	1
	a1	a2	a3	a4	a5	a6	a7	a8
0	a2	a2	a2	a5	a6	a2	a2	a2
1	a1	a3	a4	a1	a1	a7	a8	a1

Структурный синтез автомата выполняем с помощью канонического метода структурного синтеза, не выделяя явно его этапы (с целью сокращения объема примера).

Сначала проводим кодирование. Так как множества входных и выходных сигналов содержат по два элемента {0,1} каждое, то для представления каждого элемента достаточно одного двоичного символа. Считаем, что коды входных и выходных сигналов совпадают с их значениями. Так как наш автомат имеет восемь состояний, то по формуле k_сост  ]log₂|A|[ определяем, что для представления любого состояния достаточно трёх двоичных символов, следовательно нам понадобятся три триггера. Таблица кодирования состояний приведена ниже:

Таблица 2
Состояния	Код состояний	Состояния	Код состояний
a1	000	a5	010
a2	111	a6	011
a3	101	a7	110
a4	100	a8	001

Получаем структурную таблицу переходов автомата Мура.

Таблица 3. Структурная таблица переходов автомата Мура
	0	0	0	0	0	0	0	1
	000	111	101	100	010	011	110	001
0	111	111	111	010	011	111	111	111
1	000	101	100	000	000	110	001	000

Элементы памяти и базис логических элементов заданы по условию – D-триггера и булев базис.

Используя таблицу 3 и зная таблицу входов D-триггера, сразу заполняем три диаграммы Вейча для получения минимизированных функций возбуждения автомата.

	X
Q1	0	1	1	0
	0	1	1	1	Q2
	0	1	1	0
	0	0	1	1
		Q3

	X
Q1	0	0	1	1
	0	0	1	1	Q2
	0	1	1	1
	0	0	1	1
		Q3

	X
Q1	0	0	1	0
	1	1	1	1	Q2
	0	0	1	1
	0	0	1	1
		Q3

В результате минимизации получаем:

,

,

.

Используя таблицу 3 и учитывая, что у автомата Мура выходные сигналы зависят только от состояний, получаем функцию выхода автомата:

.

Используя полученные выражения для функций возбуждения и выхода автомата, и зная из теоретической части курса структурную схему автомата Мура, получаем функциональную схему автомата, которая приведена на рисунке 2.

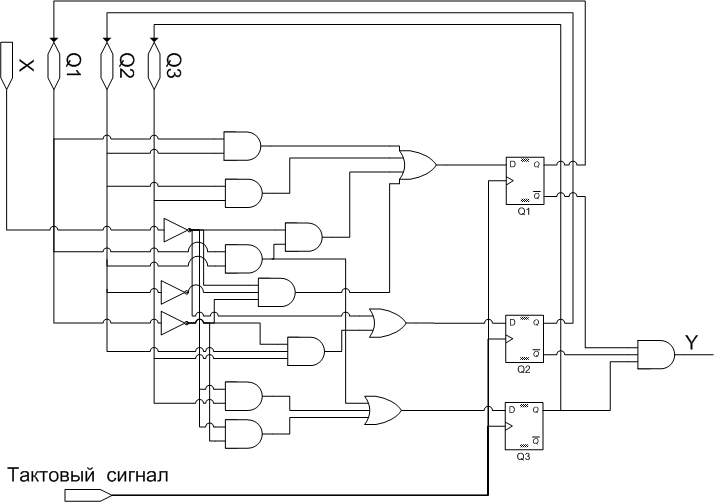
Рисунок 2. Функциональная схема автомата Мура

2-й способ. Используем модель Мили.

Вспомним, что модель состояний Мили отличается от моде­ли Мура тем, что каждому состоянию не обязательно соответст­вует только один набор выходных значений. Сигналы па выходе зави­сят не только от текущего состояния, но и от сигналов на вхо­дах, приводящих в данное состояние. На диаграмме состояний модели Мили над дугами, направленными к состоянию, указы­ваются как выходные, так и входные сигналы, которые приво­дят к переходу в данное состояние. Часто для одной и той же задачи граф автомата модели Мили имеет меньше со­стояний, чем граф автомата модели Мура, поэтому пе­ременных состояний и триггеров состояний меньше. Однако выходные функции могут иметь более сложную форму, поскольку в них используются не только переменные состояний, но и входные переменные. Существеннее то, что в случае из­менения входных сигналов в промежутках между поступления тактовых импульсов могут изменяться и значения на выходах. В зависимости от задачи это может существенно влиять (но может и не влиять) на схемное решение системы в целом.

Граф автомата модели Мили показан на рисунке 3. Разница между этим графом и графом модели Мура (рисунок 1) со­стоит в том, что состояние a₈ здесь отсутствует как таковое, а переход из состояния a₇ в состояние a₈ по приходу последнего бита последовательности заменен переходом из состояния a₇ пря­мо в состояние a₁. Теперь схема в состоянии a₁ может иметь одно из двух выходных значений: 0, если последовательность не завершена, и 1, если последовательность завершилась.

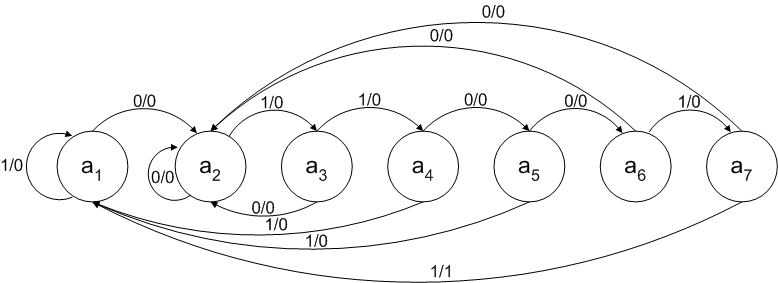
Рисунок 3. Граф автомата Мили

Графу автомата на рисунке 3 соответствует следующая совмещенная таблица переходов-выходов автомата Мили:

Таблица 3. Совмещенная таблица переходов-выходов автомата Мили
	a1	a2	a3	a4	a5	a6	a7
0	a2/0	a2/0	a2/0	a5/0	a6/0	a2/0	A2/0
1	a1/0	a3/0	a4/0	a1/0	a1/0	a7/0	A1/1

Структурный синтез автомата также выполняем с помощью канонического метода структурного синтеза. Кодирование проводим также как и для модели Мура. В итоге получаем структурную таблицу переходов-выходов автомата Мили (таблица 4).

Таблица 4. Структурная таблица переходов автомата Мили
	000	111	101	100	010	011	110
0	111/0	111/0	111/0	010/0	011/0	111/0	111/0
1	000/0	101/0	100/0	000/0	000/0	110/0	000/1

Элементы памяти и базис логических элементов заданы по условию – JK-триггера и базис И-НЕ.

Используя таблицу 4 и таблицу входов JK-триггера (которая вам известна из теоретической части курса), заполняем вспомогательную таблицу (в качестве примера только для первого триггера), которая поможет нам заполнить диаграммы Вейча для получения минимизированных функций возбуждения автомата.

	000		111		101		100		010		011		110
	J1	K1	J1	K1	J1	K1	J1	K1	J1	K1	J1	K1	J1	K1
0	1	X	X	0	X	0	X	1	0	X	1	X	X	0
1	0	X	X	0	X	0	X	1	0	X	1	X	X	1

Используя эту таблицу, заполняем две диаграммы Вейча для получения функций возбуждения J1 и K1.

	X
Q1	X	X	X	X
	X	X	X	X	Q2
	0	1	1	0
	0	X	X	1
		Q3

	X
Q1	1	0	0	1
	1	0	0	0	Q2
	X	X	X	X
	X	X	X	X
		Q3

В результате минимизации получаем:

,

.

Используя аналогичным образом полученные вспомогательные таблицы, заполняем диаграммы Вейча для получения функций возбуждения второго и третьего триггеров.

	X
Q1	0	0	1	1
	X	X	X	X	Q2
	X	X	X	X
	0	X	X	1
		Q3

	X
Q1	X	X	X	X
	1	1	0	0	Q2
	1	0	0	0
	X	X	X	X
		Q3

	X
Q1	0	X	X	0
	0	X	X	1	Q2
	0	X	X	1
	0	X	X	1
		Q3

	X
Q1	X	1	0	X
	X	0	0	X	Q2
	X	1	0	X
	X	X	X	X
		Q3

В результате минимизации получаем:

, ,

, .

Используя таблицу 4 сразу записываем функцию выхода автомата:

.

Переводим полученные выражения для функций возбуждения и выхода автомата в требуемый базис И-НЕ, используя известные вам соотношения булевой алгебры.

, ,

, ,

, ,

.

Функциональная схема автомата Мили строится по структурной схеме этого автомата. На рисунке 4 в явном виде приведена только функция выхода автомата, а функции возбуждения изображены схематично для сокращения объема примера.

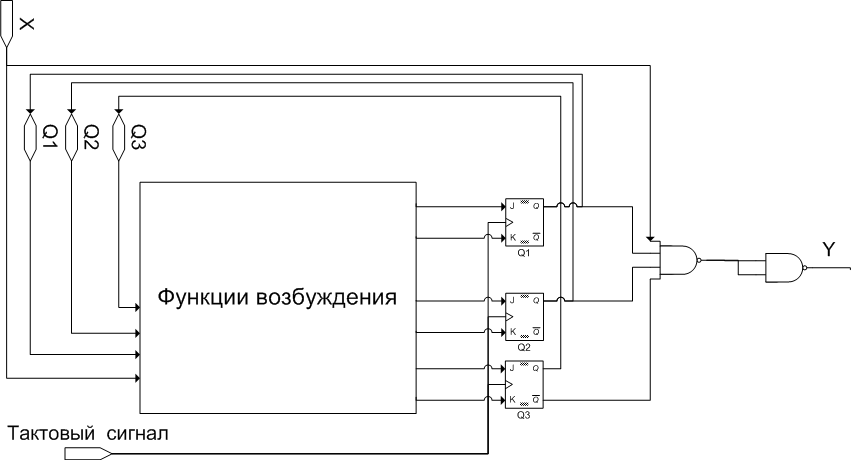
Рисунок 4. Схема автомата Мили

В вашей работе все схемы, вспомогательные таблицы и т.п. должны быть приведены полностью с необходимыми комментариями.