31.6. Непрерывные случайные величины

Если множество значений случайной величины X заполняет (непрерывно) конечный или бесконечный промежуток на число­вой оси, то такая случайная величина называется непрерывной.

Можно дать другое, более строгое, определение, используя понятие функции распределения.

Случайная величина X называется непрерывной, если ее функция распределения F(x) непрерывна на всей числовой оси.

Для непрерывной случайной величины X при любом имеет место равенство

а также

где F(x) – функция распределения величины X.

Помимо функции распределения для непрерывных случай­ных величин существует еще один удобный способ задания зако­на распределения – плотность распределения вероятностей.

Пусть функция распределения F(x) данной непрерывной случайной величины X непрерывна и дифференцируема всюду, кроме, может быть, отдельных точек.

Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функ­ции распределения:

Часто вместо термина плотность распределения исполь­зуют термины плотность вероятностей, или дифференци­альная функция, или просто плотность.

Основные свойства плотности вероятностей

Пусть f(x) – плотность вероятностей.

1.

2.

График плотности распределения вероятностей f(x) называ­ется кривой распределения.

3. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a; b), определяется равенством

4. Функция распределения F(x) выражается через плотность вероятностей f(x) формулой

Математическое ожидание непрерывной случайной ве­личины Х с плотностью распределения вероятностей f(x) находят по формуле

(31.16)

При этом математическое ожидание существует, если интеграл в правой части формулы (31.16) абсолютно сходится (это значит, что сходится интеграл

В частности, если все возможные значения принадлежат интервалу (a; b), то

Все свойства математического ожидания, указанные выше для дискретных случайных величин, сохраняются и для непре­рывных величин.

Дисперсия непрерывной случайной величины Х, возмож­ные значения которой принадлежат всей оси Ox, определяется равенством

или равносильным равенством

В частности, если все возможные значения Х принадлежат интервалу (a; b), то

или

Все свойства дисперсии, указанные для дискретных случай­ных величин, сохраняются и для непрерывных величин.

Среднее квадратичное отклонение непрерывной случай­ной величины определяется аналогичным образом, как и для дискретной величины:

На практике применяются и другие числовые характерис­тики непрерывных случайных величин.

Модой М₀(Х) непрерывной случайной величины Х называ­ется такое ее значение, при котором плотность вероятностей имеет максимум.

Медианой М_е(Х) непрерывной случайной величины Х называ­ется то ее возможное значение, которое определяется равенством

Геометрически медиану можно истолковать как точку, в ко­торой ордината f(x) делит пополам площадь, ограниченную кривой распределения.

Пример 1. Случайная величина X задана функцией распределения

Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (–1; 1).

Решение. Вероятность того, что X примет значение, заключенное в интервале (a; b), равна приращению функции распределения на этом интервале:

Положив a = –1, b = 1, получим

Пример 2. Пусть плотность вероятностей f(x) случайной величины X задана с помощью равенств

Найти коэффициент a.

Решение. Коэффициент a определяем с помощью равенства

отсюда

Пример 3. Плотность вероятностей случайной величины Х задана формулой

Найти ее числовые характеристики: математическое ожидание, дисперсию, среднеквадратическое отклонение.

Решение. Найдем математическое ожидание, используя формулу (31.16):

Вычислим дисперсию:

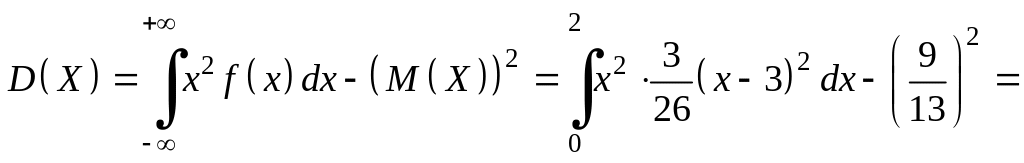
Отсюда найдем среднеквадратическое отклонение:

Задания