Контрольные вопросы
1. Опишите особенности применения линейной интерполяции.
2. Опишите особенности применения сплайн-интерполяции.
Лабораторная работа 10 Программирование в MathCad.
Цель работы: написать небольшие программы для решения тех проблем, которые не могут быть реализованы стандартными средствами.
Указания к выполнению лабораторной работы:
Для написания программ воспользуемся программной палитрой, которая имеется 10 операторов, из которых и строится программа.
Пример 1. Составим программу возвращающую 1, если число чётное и 0, если нечётное.
1. Начать создание программы с кнопки Add Line.
2. Добавить вертикальную линию, которая будет играет роль операторных скобок.
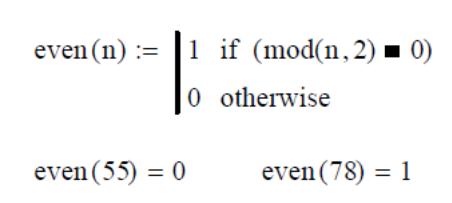
После того, как функция определена, она может использоваться наравне со встроенными функциями.
Пример 2. Более сложный пример определения максимальной координаты вектора и её позиции.
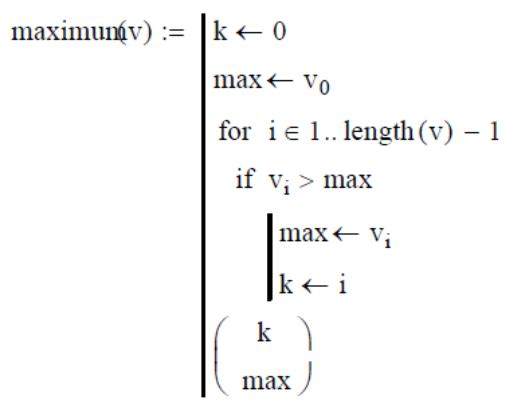
Определим теперь вектор:
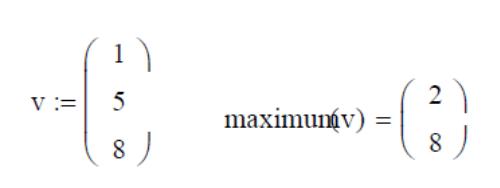
Программные
строки создаются кнопкой Add Line, операторы
вводятся соответствующей кнопкой.
Обратите внимание, что программах мы
не пользуемся оператором присваивания
:=, а вместо него пишем оператор локального
присваивания
.
Все переменные, определённые в программе, теряют своё значение при выходе из неё.
Пример 3. Рассмотрим, в качестве следующего примера, проблему вычисления несобственного интеграла.
Несложно убедиться, что попытка подставить бесконечный предел интегрирования не увенчается успехом. Например:
Этот интеграл система вычислить не смогли, но в символьном виде он считается.
Составим программу вычисления таких интегралов.
Очень интересная особенность программирования в Mathcad заключается в том, что в программе мы можем использовать операторы типа вычисления интеграла, суммы, производной и т.п.
Таблица 10.1 – Варианты задания к лабораторной работе № 10
Номер варианта |
|
|
|
Исследовать поведение функции sqrt(a,e) при отрицательных значениях a. Изменить программу так, чтобы для отрицательных значений a выводилась ошибка. |
|
|
Создать функцию, которая для произвольной матрицы вычисляет: а) минимум из максимальных элементов каждой строки; б) номер столбца, в котором расположен максимальный элемент; |
|
|
Создать функцию, которая для произвольной матрицы вычисляет: а) максимум из минимальных элементов каждой строки; б) номер строки, на которой расположен минимальный элемент; |
|
|
Создать функцию, которая для произвольной матрицы вычисляет: а) минимум из максимальных элементов каждого столбца; б) номер строки, на которой расположен максимальный элемент; |
|
|
Создать функцию, которая для произвольной матрицы вычисляет: а) максимум из минимальных элементов каждого столбца; б) количество максимальных элементов массива |
|
|
Создать функцию, которая для произвольной матрицы вычисляет: а) максимальную сумму по столбцам; б) количество минимальных элементов массива; |
|
|
Создать функцию, которая для произвольной матрицы вычисляет: а) максимальную сумму по строкам; б) количество строк, содержащих данный элемент; |
|
|
Создать функцию, которая для произвольной матрицы вычисляет: а) минимальную сумму по столбцам; б) количество столбцов, содержащих данный элемент; |
|
|
Создать функцию, которая для произвольной матрицы вычисляет: а) минимальную сумму по строкам; б) сумму минимальных элементов в каждой строке; |
|
|
Создать функцию, которая для произвольной матрицы вычисляет: а) номер столбца, в котором расположен минимальный элемент; б) сумму максимальных элементов в каждом столбце.
|
|
|
Вычислить среднее арифметическое элементов произвольной матрицы.
|
|
|
С использованием цикла while вычислить приближенное значение квадратного корня (методом касательных). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составить программу, вычисляющую факториал. Сравнить результаты с точным вычислением. |
