1. Теоретическая часть

См. теоретическую часть в лабораторно-практической работе 3.

Пример 1. Случайная величина Х имеет нормальное распределение с параметрами m = 7 и σ = 1. Найти вероятность того, что случайная величина Х принимает значения:

а) из интервала 1, 9;

б) меньшее 1;

в) большее 9;

г) отличающееся от своего среднего m по абсолютной величине не больше чем на 6.

Решение

а) Вероятность попадания нормально распределенной случайной величины Х в заданный интервал a, b определяется формулой

где Ф(x) – функция Лапласа (приложение 1).

Отсюда получаем:

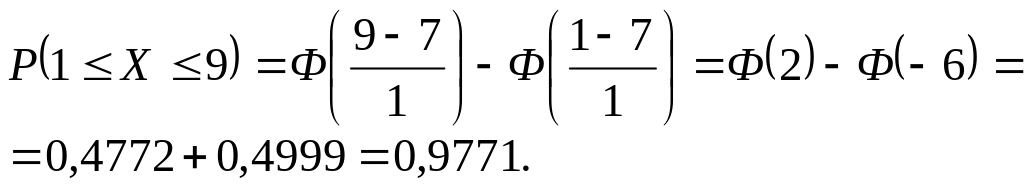
б) Вероятность того, что случайная величина Х принимает значения меньшие a, определяется формулой

Отсюда получаем:

в) Вероятность того, что случайная величина Х принимает значения большие b, определяется формулой

Отсюда получаем:

г) Вероятность отклонения случайной величины Х от среднего m не более чем на ε находится по формуле

Отсюда получаем:

2. Практическая часть

Задание 1. Случайная величина Х задана функцией распределения:

Найти:

1. плотность распределения вероятностей СВ Х ;

2. математическое ожидание, дисперсию, среднее квадратическое отклонение СВ Х;

3. построить графики функций F(x), f(x).

Значение параметра k вычислить по формуле

k = 3 + V,

где V – номер варианта.

Задание 2. Случайная величина Х задана функцией плотности распределения:

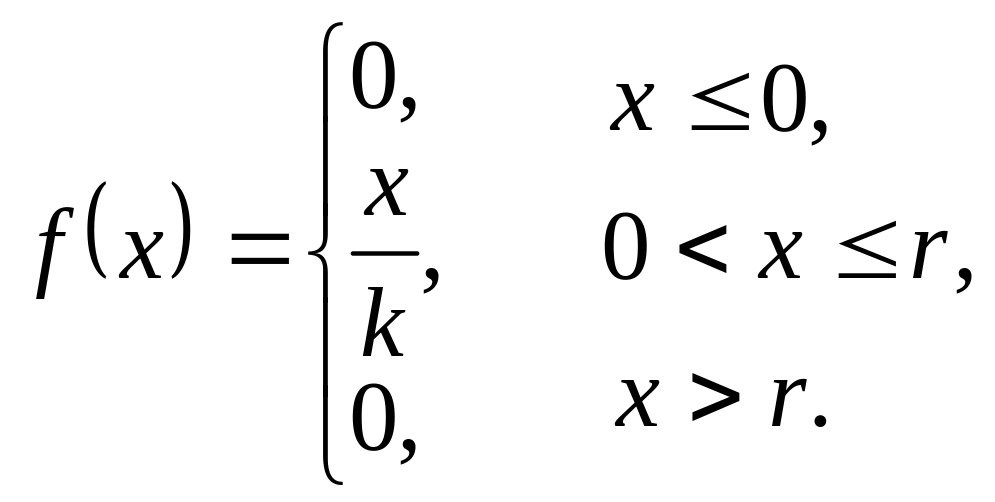
Найти:

1. функцию распределения F(x) СВ Х;

2. математическое ожидание, дисперсию, среднее квадратическое отклонение СВ Х;

3. построить графики F(x), f(x).

Значения параметров вычислить по формулам

Задание 3. Случайная величина Х имеет нормальное распределение с параметрами m, σ. Найти вероятность того, что эта случайная величина принимает значения:

1. в интервале (a, b);

2. меньшее К;

3. большее L;

4. отличающееся от своего среднего m по абсолютной величине не больше чем на ε.

П р и м е ч а н и е. Значения параметров для различных вариантов указаны в табл. 4.1.

Т а б л и ц а 4.1

Вариант	m	σ	a	b	К	L	ε
1	1	3	-1	5	-1	5	2
2	2	4	-1	8	-1	8	3
3	3	5	-1	11	-1	11	4
4	4	6	-1	14	-1	14	5
5	5	7	4	7	4	7	1
6	6	8	4	10	4	10	2
7	7	9	4	13	4	13	3
8	8	2	4	16	4	16	4
9	9	3	4	19	4	19	5
10	10	4	9	12	9	12	1
11	11	5	9	15	9	15	2
12	12	6	9	18	9	18	3
13	13	7	9	21	9	21	4
14	14	8	9	24	9	24	5
15	15	9	14	17	14	17	1
16	16	2	14	20	14	20	2
17	17	3	14	23	14	23	3
18	18	4	14	26	14	26	4
19	19	5	14	29	14	29	5
20	20	6	19	22	19	22	1
21	21	7	19	25	19	25	2
22	22	8	19	28	19	28	3
23	23	9	19	31	19	31	4
24	24	2	19	34	19	34	5
25	25	3	24	27	24	27	1
26	26	4	24	30	24	30	2
27	27	5	24	33	24	33	3
28	28	6	24	36	24	36	4
29	29	7	24	39	24	39	5
30	30	8	29	32	29	32	1

Содержание отчета

Отчет о полученных результатах должен содержать:

1. тему и цель лабораторной работы;

2. формулировку задания с указанием номера варианта;

3. решения заданий с указанием формул, используемых для вычислений;

4. графики функции распределения и плотности распределения случайной величины;

5. сведенные в таблицу результаты вычислений (с точностью до 0,001).

Контрольные вопросы

1. Какую величину называют непрерывной случайной величиной?

2. Как определяется функция распределения непрерывной случайной величины?

3. Как с помощью функции распределения вычислить вероятность того, что случайная величина Х примет значение из полуинтервала ?

4. Какими свойствами обладает функция распределения непрерывной случайной величины?

5. Какой вид может иметь график функции распределения непрерывной случайной величины?

6. Чему равна вероятность того, что непрерывная случайная величина примет одно определенное значение?

7. Можно ли утверждать, что событие А является невозможным, если Р(А) = 0?

8. Что называют плотностью распределения непрерывной случайной величины? Как ее по-другому называют?

9. Что называют кривой распределения?

10. Как с помощью плотности распределения найти вероятность попадания значений случайной величины Х в интервал (а; b)?

11. Какими свойствами обладает плотность распределения?

12. Как выражается функция распределения через плотность распределения?

13. Как выражается плотность распределения через функцию распределения?

14. Какие числовые характеристики непрерывной случайной величины вы знаете? Дайте их определения.

15. Какими свойствами обладает математическое ожидание непрерывной случайной величины?

16. Какими свойствами обладает дисперсия непрерывной случайной величины?

17. Запишите формулу нахождения дисперсии непрерывной случайной величины, принимающей значения на отрезке [а; b].

18. Запишите формулу нахождения дисперсии непрерывной случайной величины, принимающей значения на отрезке

19. Что характеризует математическое ожидание случайной величины?

20. Что характеризует дисперсия случайной величины?

21. Что такое среднее квадратическое отклонение?

22. Какие значения может принимать пуассоновская случайная величина?

23. Запишите формулу Пуассона.

24. Какой смысл имеет параметр в распределении Пуассона?

25. Чему равны математическое ожидание и дисперсия равномерно распределенной случайной величины?

26. Может ли случайная величина, распределенная по экспоненциальному закону, принимать отрицательное значение?

27. Как влияют параметры а и в нормального распределения на форму графика его плотности распределения?

Лабораторно-практическая работа 5

Вариационные ряды и их графическое изображение

Цель работы:

• приобретение навыков построения дискретных и интервальных вариационных рядов;

• графическое изображение дискретных и интервальных вариационных рядов в виде полигона и гистограммы.