Лабораторно-практическая работа 2

Теоремы сложения и умножения вероятностей

Цель работы:

• изучение действий над событиями;

• ознакомление с различными методами вычисления вероятностей событий с использованием теорем сложения и умножения вероятностей;

• практическое применение формулы полной вероятности и формул Байеса.

1. Теоретическая часть

Пусть  – пространство элементарных событий некоторого эксперимента. Подмножество А   представляет собой случайное событие. Пустое множество Ø соответствует невозможному событию, а все пространство  – достоверному событию.

Если из того, что произошло событие А, следует, что произошло и событие В, то в этом случае говорят, что из события А следует событие В, или А влечет за собой В (обозначение: А  В или В  А, т. е. А – часть В).

Если одновременно А  В и В  А, то события А и В называются равносильными, или эквивалентными. Эквивалентные события состоят из одних и тех же элементарных событий (обозначение: А = В).

Суммой событий А и В называется такое событие, которое состоится при появлении либо события А, либо события В, либо обоих событий вместе (обозначение: А + В или А  В).

Произведением событий А и В называется такое событие, которое происходит при одновременном наступлении обоих событий (обозначение: или ).

Разностью событий А и В называется событие, которое состоится, если событие А произойдет, а событие В не произойдет (обозначение: или ).

События А и В называются несовместными, если их совместное наступление исключено, т. е.

Ø. (2.1)

Событие, состоящее в ненаступлении события А, называют событием, противоположным событию А, и обозначают через . Оно определяется двумя равенствами: Ø и .

Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или не произошло.

Теорема 1

Вероятность произведения двух независимых событий равна произведению их вероятностей:

. (2.2)

Теорема 2

Если А и В – независимые события, то независимы также события: и , и , и .

События называются попарно независимыми, если любая пара независима, т. е.

. (2.3)

События называются независимыми в совокупности, если при любом выборе k различных событий ( ) из данной совокупности выполняется равенство

. (2.4)

Например, если события А, В и С независимы в совокупности, то независимы события А и В, В и С, А и С, В и АС, А и ВС, С и АВ.

Из независимости событий в совокупности следует их попарная независимость. Однако попарная независимость событий не гарантирует их независимости в совокупности.

Теорема 3

Если события независимы в совокупности, то верно равенство

. (2.5)

Теорема 4

Если события независимы в совокупности, то верно равенство

. (2.6)

Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Вероятность события В, вычисленная при условии, что имело место другое событие А, называется условной вероятностью события В (обозначение: Р(В│А)).

Условная вероятность определяется равенством:

(2.7)

где Р(А) > 0.

Аналогично,

, Р(В) > 0. (2.8)

Теорема 5 (формула умножения вероятностей двух совместных событий)

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло, т. е.

Р(АВ) = Р(В│А) · Р(А) = Р(А│В) · Р(В). (2.9)

Эта формула имеет смысл, когда события А и В совместны. По определению, событие В не зависит от события А, если Р(В│А) = Р(В). В этом случае также Р(А│В) = Р(А), т. е. событие А не зависит от события В.

Теорема 6 (формула умножения вероятностей n совместных событий)

Вероятность произведения n совместных событий равна произведению вероятности одного из них на условные вероятности всех остальных в предположении, что все предыдущие события наступили, т. е.

Р(А₁·А₂·…·А_n)=Р(А₁) Р(А₂│А₁) Р(А₃│А₁А₂) Р(А_n│А₁·А₂·А_n-1). (2.10)

Для трех событий А, В, С эта формула имеет вид:

Р(АВС) = Р(А) Р(В│А) Р(С│АВ). (2.11)

Гипотезами будем называть попарно несовместные события Н₁, Н₂, …, Н_n, образующие полную группу событий, причем Р(Н_i) 0, i = .

Пусть А – произвольное событие Н_i (i = ), причем А  Н₁ + Н₂ + … + Н_n (рис. 2.1).

Вероятности событий Н_i (i = ) известны, т. е. известны Р(Н₁), Р(Н₂), …, Р(Н_n). Также известны условные вероятности Р(А|Н₁), Р(А|Н₂), …, Р(А|Н_n). Вероятность события А вычисляется по формуле полной вероятности:

(2.12)

Н1

Н2

А

Нn

Рис. 2.1

Пусть Н₁, Н₂, …, Н_n – попарно-несовместные события, вероятности которых Р(Н_i)  0, (i = ), событие А является случайным, причем А  Н₁ + Н₂ + … + Н_n. Пусть также известны условные вероятности Р(А|Н_i) (i = ). Произведен опыт, в результате которого появилось событие А. Условные вероятности событий Н₁, Н₂, …, Н_n относительно события А вычисляются по формулам Байеса:

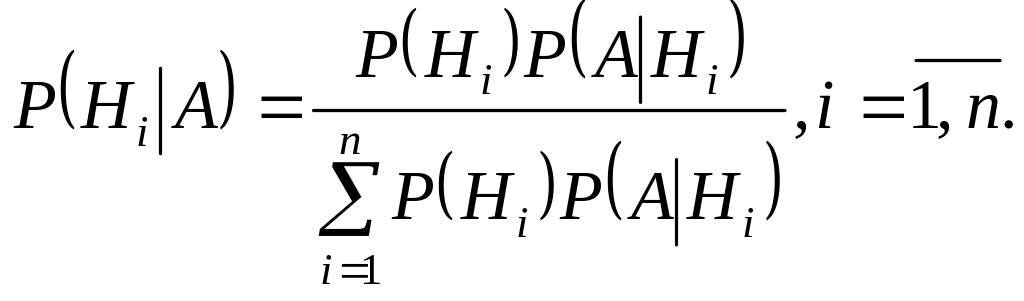(2.13)

Вероятности Р(Н_i) (i = ) событий Н₁, Н₂, …, Н_n до опыта называют априорными вероятностями.

Вероятности Р(Н_i|А) (i = ) событий Н₁, Н₂, …, Н_n называют апостериорными вероятностями.

Пример 1. Имеется 2 урны, в первой – 2 белых и 3 черных шара, во второй – 4 белых и 2 черных. Из каждой урны вынимается по одному шару. Найти вероятность того, что они будут одного и того же цвета.

Решение. Рассмотрим событие А – оба шара одного цвета – как сумму двух других событий: А₁ – оба шара белые и А₂ – оба шара черные, т. е. . При этом событие А₁ можно представить как произведение независимых событий В₁ и В₂, где В_i – из i-й урны вынут белый шар (i = 1, 2): . Аналогично, , где события С_i – из i-й урны вынут черный шар (i = 1, 2), также являются независимыми. Применяя правило умножения вероятностей двух независимых событий, имеем следующее:

;

.

Так как события А₁ и А₂ несовместны, то применим правило сложения вероятностей:

.

Ответ: 7/15.

Пример 2. Вероятность того, что будет снег, равна 0,7, а того, что будет дождь, – 0,35. Определить вероятность плохой погоды, если вероятность дождя со снегом равна 0,15.

Решение. Рассмотрим следующие события: событие А – будет снег; событие В – будет дождь. Тогда событие АВ – будет снег с дождем, а событие А + В – будет либо дождь, либо снег, либо то и другое одновременно, т. е. будет плохая погода.

Р(А + В) = Р(А) + Р(В) – Р(АВ).

Поэтому Р(А + В) = 0,7 + 0,35 – 0,15 = 0,9.

Ответ: 0,9.

Пример 3. На сборку механизма поступают детали из двух автоматов. Первый автомат в среднем дает 1,5 % брака, второй – 1 %. С первого автомата поступило 2000 деталей, а со второго – 1500.

а) Найти вероятность попадания на сборку бракованной детали.

б) Наугад взятая деталь оказалась бракованной. Найти вероятность того, что она изготовлена на первом автомате.

Решение.

а) Рассмотрим гипотезы: – деталь, поступившая на сборку механизма, произведена на первом автомате; – деталь, поступившая на сборку механизма, произведена на втором автомате. Тогда , . Вероятность того, что бракованная деталь произведена на первом автомате, равна , так мы учли процент брака для первого автомата. Аналогично, вероятность того, что бракованная деталь произведена на втором автомате, равна Для того, чтобы найти вероятность события А – выбранная наудачу деталь из числа поступивших на сборку оказалась бракованной – применим формулу полной вероятности:

б) Чтобы найти вероятность того, что наугад взятая деталь, будучи бракованной, изготовлена на первом автомате, надо применить формулу Байеса:

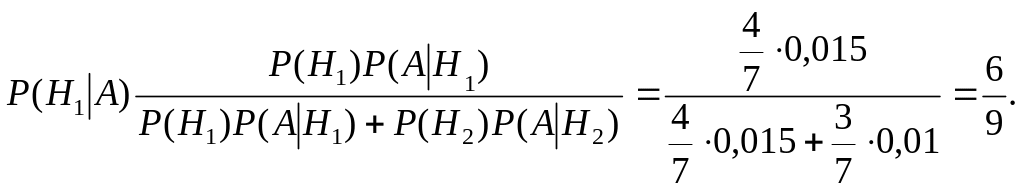
Ответ: а) 0,0129; б) 0,67.

Теоретическое задание. Написать формулу вероятности суммы двух независимых событий.