
- •Теория вероятностей и математическая статистика
- •Лабораторно-практическая работа 1
- •1. Теоретическая часть
- •2. Практическая часть
- •Лабораторно-практическая работа 2
- •1. Теоретическая часть
- •2. Практическая часть
- •Лабораторно-практическая работа 3
- •1. Теоретическая часть
- •2. Практическая часть
- •Задание 3. На телефонной станции неправильное соединение происходит с вероятностью р. Найти вероятность того, что среди n соединений имеет место:
- •1. Теоретическая часть
- •2. Практическая часть
- •1. Теоретическая часть
- •2. Практическая часть
- •1. Теоретическая часть
- •1.1. Статистические оценки параметров распределения
- •1.2. Доверительный интервал
- •1.3. Определение объема выборки
- •2. Практическая часть
- •1. Теоретическая часть
- •1.1. Проверка параметрических гипотез
- •1.2. Проверка непараметрических гипотез
- •2. Практическая часть
- •Выборки для задач математической статистики
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Теория вероятностей и математическая статистика
- •220005, Г. Минск, пр-т Независимости, 62.
1.2. Доверительный интервал
Доверительный интервал – это интервал , который покрывает неизвестный параметр θ с заданной надежностью γ.
Построение доверительных интервалов для числовых характеристик нормальной генеральной совокупности. Пусть генеральная совокупность имеет нормальное распределение.
Доверительный интервал для генеральной средней а имеет вид:
![]() (6.5)
(6.5)
где – выборочная средняя;
S – стандартное отклонение, полученное по выборке;
n – объем выборки;
![]() – значение
распределения Стьюдента с (n
– 1) степенями свободы для двусторонней
критической области с α
= 1 – γ,
– значение
распределения Стьюдента с (n
– 1) степенями свободы для двусторонней
критической области с α
= 1 – γ,
где γ – доверительная вероятность.
Значение
![]() – называется предельной
ошибкой выборки.
– называется предельной
ошибкой выборки.
Доверительный
интервал для дисперсии
![]() генеральной совокупности имеет вид:
генеральной совокупности имеет вид:
![]() (6.6)
(6.6)
где n – объем выборки;
S2 – исправленная выборочная дисперсия;
U1 и U2 – значения из таблицы 2 с (n – 1) степенями свободы при условии, что
![]()
![]()
Доверительный интервал для среднего квадратического отклонения генеральной совокупности имеет вид:
![]() (6.7)
(6.7)
где S – стандартное отклонение;
n – объем выборки, значения U1 и U2 находятся по таблице 2 с (n – 1) степенями свободы из условия, что
1.3. Определение объема выборки
Иногда нужно проводить исследования с заданной точностью . В этом случае необходимо рассчитать объем выборки по формуле:
![]() (6.8)
(6.8)
где – значение распределения Стьюдента с (n – 1) степенями свободы для двусторонней критической области с α = 1 – γ,
где γ – доверительная вероятность;
S2 – исправленная выборочная дисперсия;
– точность оценки.
Пример
1.
Вычислить по выборке F3
несмещенные оценки генеральной средней
а,
дисперсии 2
и среднего квадратического отклонения
:
![]() S2,
S.
S2,
S.
Исходные данные:
F3: 114, 105, 103, 122, 118, 113, 107
Решение
1. Вычислим по данным вариационного ряда F3 выборочную среднюю которая является несмещенной оценкой генеральной средней по формуле:
![]()
![]()
2. Вычислим по данным вариационного ряда F3 исправленную дисперсию S2, которая является несмещенной оценкой генеральной дисперсии по формуле:
где n – объем выборки;
DB – выборочная дисперсия.
![]()

![]()
откуда
![]()
3. Вычислим по данным вариационного ряда F3 стандартное отклонение S, которое является несмещенной оценкой генерального среднего квадратического отклонения по формуле:
![]()
Имеем
![]()
Пример 2. Построить доверительные интервалы для средней а, дисперсии 2 и среднего квадратического отклонения генеральной совокупности при доверительной вероятности γ = 0,8 по данным выборки F3.
Решение
1. Построим доверительный интервал для средней генеральной совокупности, пользуясь формулой:
![]()
где – выборочная средняя;
S – стандартное отклонение, полученное по выборке;
n – объем выборки;
– значение распределения Стьюдента с (n – 1) степенями свободы для двусторонней критической области с α = 1 – γ,
где γ – доверительная вероятность.
В
нашем случае
![]() доверительная вероятность γ
= 0,8,
α
= 1 – 0,8 = 0,2, n
= 7, S
= 7,01.
доверительная вероятность γ
= 0,8,
α
= 1 – 0,8 = 0,2, n
= 7, S
= 7,01.
Из
таблицы распределения Стьюдента
(приложение 3) для двусторонней критической
области найдем
![]() Далее находим предельную ошибку выборки:
Далее находим предельную ошибку выборки:
![]()
и строим доверительный интервал:
(111,7 – 3,8; 111,7 + 3,8).
(107,9; 115,5).
2. Доверительный интервал для дисперсии 2 генеральной совокупности строим по формуле:
где n – объем выборки;
S2 – исправленная выборочная дисперсия;
U1 и U2 – значения из таблицы 2 с (n – 1) степенями свободы (приложение 4) при условии, что
Имеем n = 7, S2 = 49,2, число степеней свободы равно n – 1 = = 7 – 1 = 6.
![]() тогда
тогда
![]()
![]() тогда
тогда
![]()
Строим доверительный интервал:

(27,73; 133,94).
3. Доверительный интервал для среднего квадратического отклонения генеральной совокупности получаем, извлекая квадратные корни из концов доверительного интервала для дисперсии.
Если доверительный интервал для дисперсии имеет вид: (27,73 < 2 < 133,94), то доверительный интервал для среднего квадратического отклонения будет:
![]()
(5,27; 11,57).
Пример 3. Считая выборку F3 пробной, определить минимальный объем выборки n для нахождения доверительного интервала для среднего значения а генеральной совокупности с точностью = 2 и доверительной вероятностью = 0,9.
Решение. Рассчитываем объем выборки по формуле:
![]()
По
условию задачи имеем S2
= 49,2, 2
= 4, значение
![]() находим из таблицы распределения
Стьюдента (приложение 3) с n –
1 = 7 – 1 = 6 степенями свободы для двусторонней
критической области с α
= = 1 – γ
= 1 – 0,9 = 0,1, получим
находим из таблицы распределения
Стьюдента (приложение 3) с n –
1 = 7 – 1 = 6 степенями свободы для двусторонней
критической области с α
= = 1 – γ
= 1 – 0,9 = 0,1, получим
![]() Откуда
Откуда
![]()
Пример 4. С помощью табличного процессора Excel найти по выборке Х несмещенные оценки генеральной средней а, дисперсии 2 и среднего квадратического отклонения и доверительный интервал для среднего значения генеральной совокупности с надежностью = 0,8.
Решение. Пусть имеем выборку Х:
29, 30, 30, 32, 30, 30, 29, 31, 30, 29, 29, 29, 30, 29, 28, 29, 29, 27, 27, 28, 32, 29, 31, 33.
Для вычисления точечных оценок , S2, S и построения доверительного интервала для генеральной средней в программе Excel надо использовать инструмент Пакета анализа средство Описательная статистика (рис. 6.1).
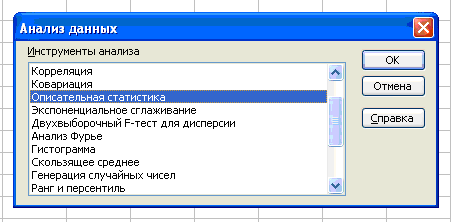
Рис. 6.1
Вводим в лист таблицы Excel исходные данные, ставим флажок в поле Итоговая статистика и указываем в поле Уровень надежности заданную надежность = 0,8 (рис. 6.2).
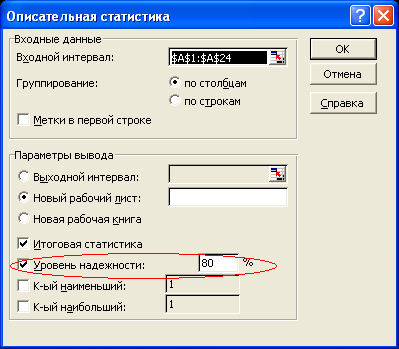
Рис. 6.2
Получаем результаты расчета, которые изображены на рис. 6.3.
Проанализируем
полученные результаты. На рис. 6.3. видно,
что выборочная средняя (среднее)
![]() исправленная дисперсия (дисперсия
выборки)
S2
= 2,166666667; стандартное отклонение S
=1,471960144; размах выборки (интервал)
равен 6, объем выборки (счет)
равен
24. В строке Уровень
надежности
находится предельная ошибка выборки
= 0,396448633, с помощью которой формируется
доверительный интервал
исправленная дисперсия (дисперсия
выборки)
S2
= 2,166666667; стандартное отклонение S
=1,471960144; размах выборки (интервал)
равен 6, объем выборки (счет)
равен
24. В строке Уровень
надежности
находится предельная ошибка выборки
= 0,396448633, с помощью которой формируется
доверительный интервал
![]() Потому доверительный интервал имеет
вид (29,58333333 – 0,396448633; 29,58333333 + 0,396448633).
Округляя значения, получим доверительный
интервал (29,187; 29,979) для среднего значения
генеральной совокупности с надежностью
= 0,8.
Потому доверительный интервал имеет
вид (29,58333333 – 0,396448633; 29,58333333 + 0,396448633).
Округляя значения, получим доверительный
интервал (29,187; 29,979) для среднего значения
генеральной совокупности с надежностью
= 0,8.
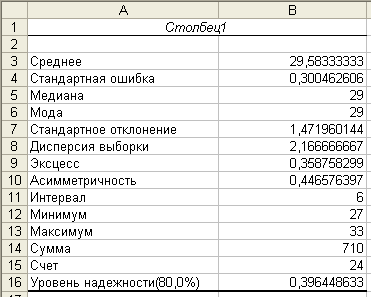
Рис. 6.3
