Теория вероятностей и математическая статистика

Практикум

Предисловие

Настоящее пособие составлено в соответствии с программой предмета «Теория вероятностей и математическая статистика». В него включены лабораторно-практические работы по следующим разделам:

- «Классическое, геометрическое и статистическое определения вероятностей событий»;

- «Теоремы сложения и умножения вероятностей»;

- «Законы распределения дискретных случайных величин»;

- «Непрерывные случайные величины: законы распределения и числовые характеристики»;

- «Вариационные ряды и их графическое изображение»;

- «Точечные и интервальные оценки параметров распределения»;

- «Проверка статистических гипотез».

Цель пособия – помочь учащимся ознакомиться с теоретическим материалом, приобрести навыки решения задач по теории вероятностей, а также освоить статистические методы обработки данных, имеющие широкое прикладное значение.

В каждой лабораторно-практической работе приведен теоретический материал по теме работы, даны решения типовых задач и предложено 30 вариантов индивидуальных заданий. Учащемуся указывается его номер варианта, который соответствует порядковому номеру в журнале и не меняется при выполнении каждой последующей работы. При выполнении работы рекомендуется придерживаться следующего порядка:

1. ознакомиться с теоретической частью;

2. записать тему и цель работы;

3. указать вариант;

4. переписать условия задач;

5. выполнить задания в предложенном порядке;

6. составить отчет по лабораторно-практической работе (содержание отчета указано в конце каждой работы).

Контроль за выполнением индивидуальных заданий осуществляется преподавателем в форме зачета, на котором учащийся должен ответить на теоретические вопросы из списка, предложенного в конце каждой работы, пояснить решение и продемонстрировать умение решать аналогичные задачи. В результате учащемуся выставляется зачет или незачет по каждой лабораторно-практической работе отдельно. Лабораторно-практические работы по теории вероятностей предполагают самостоятельное аудиторное решение предложенных заданий, а по математической статистике проводятся в компьютерном классе с применением пакета электронных таблиц Excel.

Пособие может быть полезно преподавателям при проведении лабораторно-практических занятий из-за большого числа задач, носящих прикладной характер.

Лабораторно-практическая работа 1

Классическое, геометрическое и статистическое

определения вероятностей событий

Цель работы:

• изучение основных понятий теории вероятностей;

• ознакомление с различными методами вычисления вероятностей событий;

• практическое применение элементов комбинаторики для вычисления вероятностей событий.

1. Теоретическая часть

Теория вероятностей – это раздел математики, в котором изучаются случайные явления (события) и выявляются закономерности при их массовом повторении.

Комбинаторика – это раздел математики, в котором решаются задачи, связанные с рассмотрением множеств, составлением различных комбинаций из элементов этих множеств и определением правила подсчета числа таких комбинаций.

Пусть дано множество Е, содержащее n элементов. Число n называют объемом множества Е.

Извлечение m ( ) элементов из множества Е называется выбором m элементов, а сам извлеченный набор – выборкой объема n.

Теорема 1 (основной принцип перечисления)

Если множество Е₁ содержит n₁ элементов, а множество Е₂ содержит n₂ элементов, …, множество Е_к содержит n_к элементов, то число способов выбора по одному элементу из каждого множества Е₁, Е₂, …, Е_к равно

Следствие

Если множества Е₁, Е₂, …, Е_к содержат по n элементов каждое, то число способов выбора по одному элементу из этих множеств равняется

Перестановкой n элементов называется расположение этих элементов в определенном порядке. Число перестановок из n элементов определяется формулой

. (1.1)

Любой выбор m элементов, взятых в определенном порядке, из n элементов, называется размещением из n по m. Число размещений из n по m элементов равно

. (1.2)

Любой выбор m элементов из n элементов без учета порядка выбора называется сочетанием из n по m. Число сочетаний из n по m равно

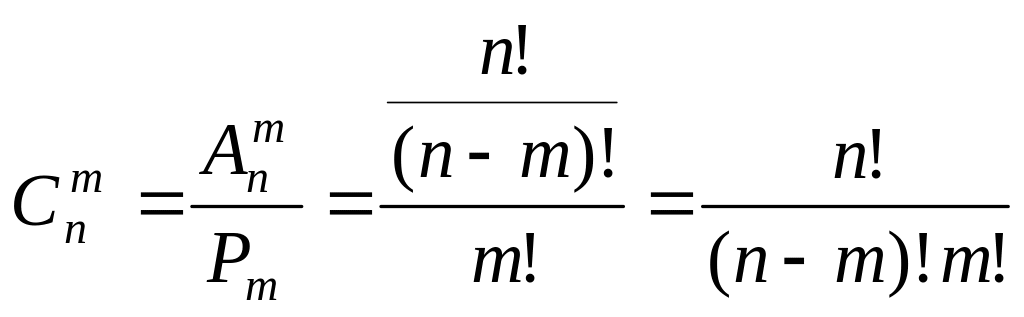. (1.3)

Одна из типовых задач состоит в подсчете числа способов разложения множества Е объемом n на k групп с фиксированным числом элементов в каждой группе. Пусть множество Е содержит n элементов и его необходимо разбить на k подмножеств Е₁, Е₂, …, Е_k, каждое из которых содержит соответственно n₁, n₂, …, n_k элементов, причем . Число разбиений подобного рода равно

. (1.4)

Будем называть опытом, или экспериментом, или испытанием, всякое осуществление определенного комплекса условий или действий, при которых наблюдается соответствующее явление. Возможный результат опыта называется событием.

Событие называется достоверным в данном опыте, если в этом опыте оно обязательно произойдет.

Событие называется невозможным, если в данном опыте оно произойти не может (обозначение: Ø).

Случайным событием называется событие, которое в данном опыте может произойти, а может и не произойти (обозначение: A, B, C, D, …).

Элементарным событием будем называть исход одного испытания, т. е. это такое событие, которое невозможно разложить на более простые события. Все остальные события называются составными. Таким образом, каждое составное событие представляет собой сумму элементарных событий.

Множество всех возможных исходов одного испытания или, другими словами, множество всех элементарных событий называется пространством элементарных событий (обозначение: ).

События называются несовместными, если появление одного из них исключает появление других событий в условиях одного и того же эксперимента.

Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Событие, противоположное событию А, будем обозначать .

Два события называются совместными в данном опыте, если появление одного из них не исключает появление другого в этом же опыте.

Множество событий А₁, А₂, …, А_n называют полной группой событий, если они попарно несовместны, т. е. несовместны А_i и А_j, где i = 1, 2, …, n; j = 1, 2, …, n, i j, и если в результате испытаний обязательно произойдет хотя бы одно из этих событий, т. е. одно из событий А_i будет достоверным (i = 1, 2, …, n).

События называются равновозможными, если нет оснований полагать, что одно событие является более возможным, чем другие.

Под вероятностью события понимается некоторая числовая характеристика возможности наступления этого события.

Пусть при проведении n испытаний некоторое событие А появилось m раз. Многочисленные эксперименты такого рода показывают, что при больших n отношение , называемое относительной частотой события А, остается примерно постоянным, т. е. событие А обладает так называемой статистической устойчивостью.

Статистическое определение вероятности заключается в том, что за вероятность события А принимается постоянная величина, вокруг которой колеблются значения относительной частоты при неограниченном возрастании числа n.

Для существования статистической вероятности события А требуется:

а) возможность производить неограниченное число испытаний, в каждом из которых событие А наступает или не наступает;

б) устойчивость относительных частот появления события А в различных сериях достаточно большого числа испытаний.

Классической схемой называется испытание, при котором число элементарных исходов конечно и все из них равновозможны.

Элементарные исходы, при которых данное событие наступает, называют благоприятствующими этому событию, или благоприятными исходами.

Рассмотрим конечное множество равновозможных элементарных исходов , образующих полную группу событий, т. е. , при . Пусть событие А наступает при появлении некоторых из этих элементарных исходов , где и не наступает при появлении других (т. е. перечисленные исходы являются благоприятствующими событию А).

Классической вероятностью события А называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных, образующих полную группу элементарных исходов опыта, в котором может появиться это событие.

Вероятность события А обозначают через Р(А). Тогда, по определению,

, (1.5)

где m – число благоприятных событию А исходов;

n – число всех равновозможных элементарных исходов опыта, в котором может появиться событие А.

Построение логически полноценной теории вероятностей основано на аксиоматическом определении случайного события и его вероятности. В системе аксиом, предложенной А. Н. Колмогоровым, неопределяемыми понятиями являются «элементарное событие» и «вероятность». Аксиомы, определяющие вероятность:

1. каждому событию А поставлено в соответствие неотрицательное действительное число Р(А), называемое вероятностью события А;

2. вероятность достоверного события равна единице, т. е.

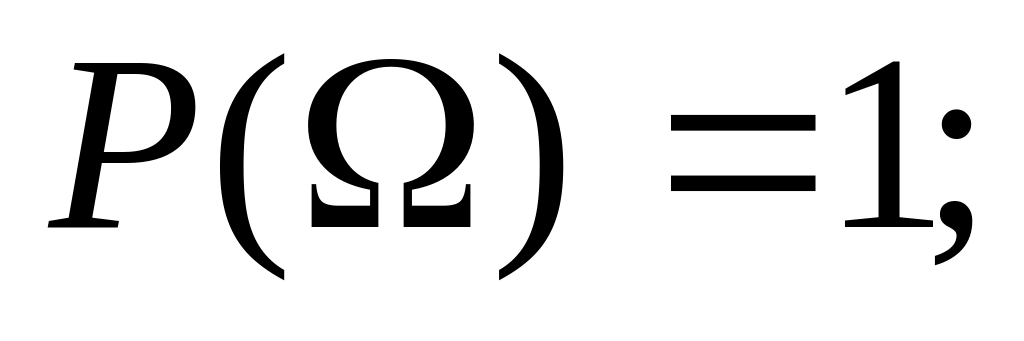
3. вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий.

Исходя из этих аксиом, свойства вероятностей и зависимости между ними выводятся в качестве теорем.

Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике весьма часто встречаются испытания, число возможных исходов которых бесконечно. В таких случаях классическое определение неприменимо. Чтобы преодолеть недостаток классического определения вероятности, вводят понятие геометрической вероятности.

Общая задача, приведшая к необходимости расширения понятия вероятности, в случае плоскости имеет следующую формулировку. Пусть на плоскости задана некоторая область D, площадь которой равна S(D). В области D содержится область G площадью S(G). Рассматриваемое событие А состоит в попадании точки, наугад брошенной в область D, в область G. При этом любое расположение точки в области считается равновероятным.

Тогда отношение

(1.6)

называется геометрической вероятностью события А, т. е. вероятностью того, что в результате испытания случайная точка попадет в область G.

Аналогично вводится понятие геометрической вероятности при бросании точки на отрезок или в пространственную область. При этом вводят понятие меры области, которая представляет собой длину в случае, когда область является отрезком, либо площадь плоской области, либо объем пространственного тела. Обозначим меру области D через mes(D), а меру области G через mes(G). Тогда вероятность попадания в область G точки, брошенной в область D, по определению геометрической вероятности, выражается формулой

. (1.7)

Пример 1. Сколькими способами можно расселить 9 студентов по трем комнатам: двухместной, трехместной, четырехместной?

Решение. Найдем

Ответ: 1260.

Пример 2. В урне 10 лотерейных билетов, из них 4 выигрышных. Из урны наугад извлекаются два билета. Найти вероятность того, что: а) оба билета выигрышные (событие А); б) оба билета без выигрыша (событие В); в) один билет выигрышный, а другой нет (событие С).

Решение.

а) Выбор двух билетов из 10 можно осуществить n = = 45 способами, а двух выигрышных билетов из четырех = = 6 способами. Тогда Р(А) = /n = 6/45 = 2/15.

б) Имеются = = 15 возможностей выбора билета без выигрыша. В таком случае вероятность Р(В)= /n = 15/45 = 1/3.

в) Существуют 4 возможности вытащить выигрышный билет и 6 возможностей – билет без выигрыша. Имеются = 6  4 = 24 возможности вытащить один билет с выигрышем, а другой без выигрыша. Тогда Р(С) = /n = 24/45 = 8/15.

Ответ: а) 2/15; б) 1/3; в) 8/15.

Пример 3. В области D, ограниченной эллипсоидом

,

наудачу зафиксирована точка. Какова вероятность того, что ее координаты будут удовлетворять неравенству ?

Решение. Введем в рассмотрение событие А – наудачу зафиксированная в области D точка попала в область, ограниченную сферой . По определению геометрической вероятности,

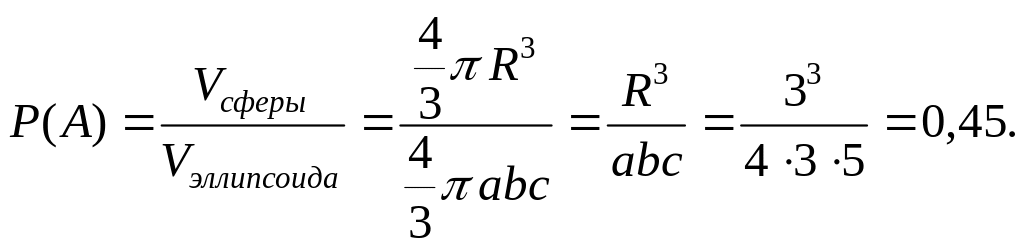
Ответ: 0,45.