Задача 1

Основой задачи является схема, приведенная на рис. 1.

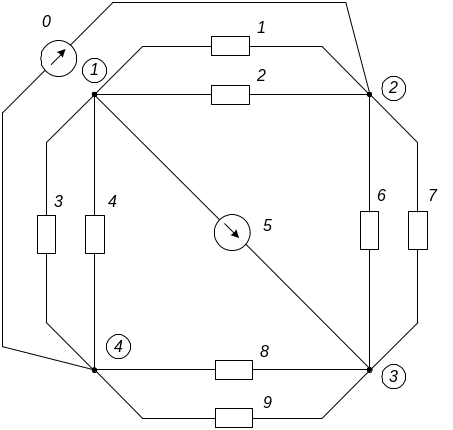
Рис. 1

В ней пронумерованы узлы и ветви. Номера узлов обведены. Схема состоит из резисторов и источников напряжения.

Перед решением задачи из этой схемы необходимо удалить две ветви. Номер одной такой ветви равен предпоследней цифре, а номер другой – последней цифре номера зачетной книжки. Если вторая цифра совпадает с первой, то вторую ветвь следует удалить по выбору студента. Затем ветви необходимо перенумеровать, начиная с номера 1 и кончая номером 8.

Для полученной в результате указанного упрощения схемы необходимо:

а) выбрать условно положительные направления ветвей;

б) построить направленный граф;

в) сформулировать редуцированную матрицу инциденций;

г) определить дерево графа;

д) сформулировать матрицу главных сечений и матрицу главных контуров.

Указания к задаче 1

Определение дерева графа необходимо выполнить по алгоритму, основанному на преобразовании редуцированной матрицы инциденций. Преобразование выполняется по методу исключения Гаусса или по методу Жордана-Гаусса. В первом случае соответствующая подматрица матрицы инциденций преобразуется в верхнюю треугольную, а во втором случае – в единичную. Преобразование выполняется для того, чтобы выявить линейно независимые столбцы матрицы инциденций. Именно такие столбцы соответствуют ветвям, составляющим дерево графа.

Если используется метод исключения Гаусса, то для формирования матрицы главных сечений нужны дополнительные преобразования матрицы инциденций по методу Жордана-Гаусса. Если же использутся метод Жордана-Гаусса, то одновременно определяется дерево и формируется матрица главных сечений.

Матрица главных контуров формируется на основании матрицы главных сечений.

Задача 2

Основой задачи является схема, приведенная на рис. 2.

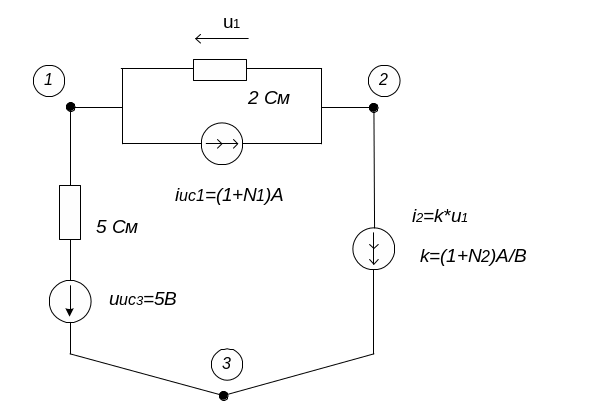
Рис. 2

В схеме имеется три узла, номера которых обведены, и три обобщенные ветви. В схему включены два резистора с проводимостью соответственно 2 и 5 Ом, независимый источник напряжения с напряжением 5 В, независимый источник тока с током i_ис1 и источник тока, управляемый напряжением, ток которого обозначен через i₂.

Ток независимого источника тока определяется обозначенной через N1 предпоследней цифрой номера зачетной книжки. Так, если эта цифра равна 5, то ток источника в соответствии с формулой, приведенной на схеме, равен 6 А.

Коэффициент k, являющийся параметром источника тока, управляемого напряжением, определяется обозначенной через N2 последней цифрой номера зачетной книжки. Так, если эта цифра равна 9, то коэффициент в соответствии с формулой, приведенной на схеме, равен 10 А/В, т. е. 10 сименсов.

Для схемы, полученной в результате указанной конкретизации параметров, необходимо:

а) записать в матричной форме систему узловых уравнений;

б) выполнить прямое формирование матрицы проводимости узлов и столбца эквивалентных узловых источников тока;

в) решить систему узловых уравнений.

Указания к задаче 2

В качестве опорного выбрать узел номер 3.

Для получения системы узловых уравнений в матричной форме вначале необходимо сформировать редуцированную матрицу инциденций А, матрицу проводимостей ветвей Y_B,столбец токов независимых источников тока i_ИС, столбец напряжений независимых источников напряжения u_ИС.

Затем матрица узловых проводимостей Y_УЗ вычисляется в соответствии с выражением Y_УЗ=А* Y_B*А', где А' – матрица А после транспонирования. Столбец эквивалентных узловых источников тока i_УЗ вычисляется в соответствии с выражением i_УЗ=А* i_ИС - А* Y_B* u_ИС.

Прямое формирование матрицы проводимостей узлов и столбца эквивалентных узловых источников тока следует выполнять по шагам, при переходе от одной обобщённой ветви к другой. Матрицу и столбец следует представлять после каждого шага.

Необходимо убедиться, что прямое формирование даёт тот же результат, что и формирование по матричному выражению.

Решение полученной системы следует выполнить по методу исключения Гаусса. Так как в системе всего два неизвестных, то это не представляет затруднений.