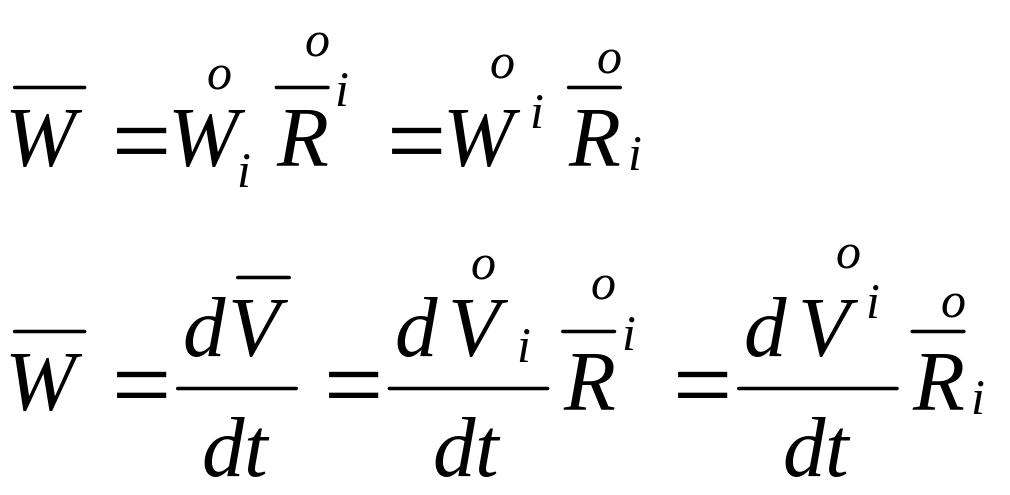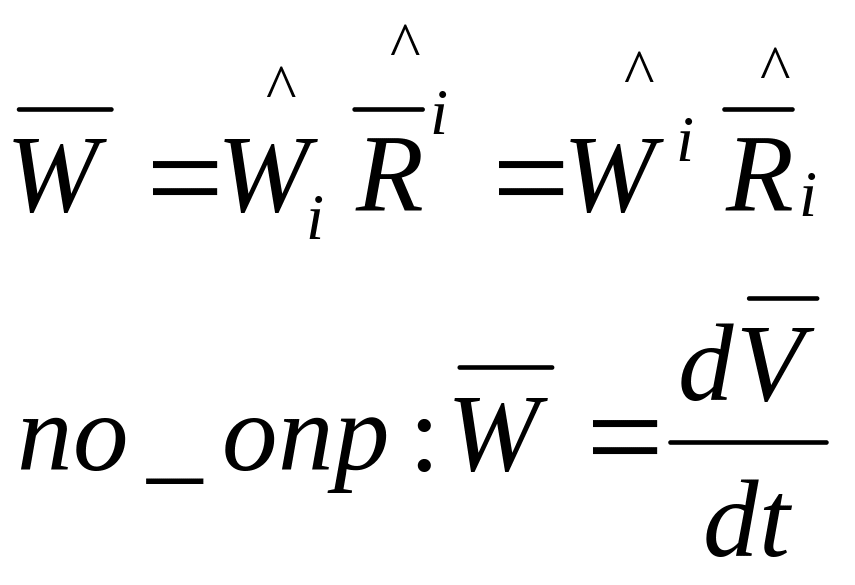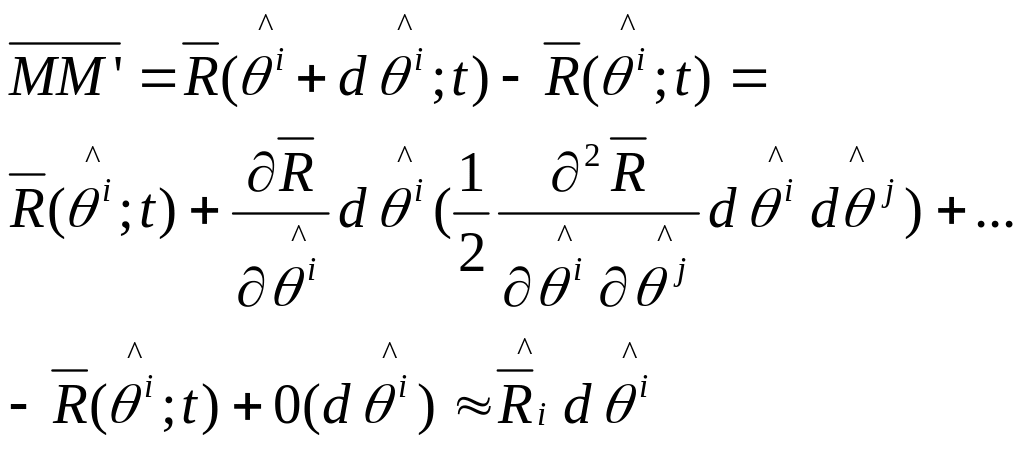1.Материальные и пространственные координаты точек сплошной среды. Закон движения, траектории, линий тока.

Р-им Евкл. 3хмерное пр-во т.е. можно для всего пр-ва ввести единую ортонорм. Ск с базисом , и корд-ми :

Можно задать зависимости:

, такие, что (определитель Якоби), т.е. - крив. СК. Этой СК отвечают базисные в-ы ; метр.тенз - диск. тенз - , символы Кристофеля

СК - декарт; - крив. СК наз. пространственными.

Введем другие СК с использование движущейся среды:

Пусть в момент зафиксир-н объект. Состояние СС в начале дв-ия ( ) будем наз. отчет. конфигурацией.

М-матер.т-а. Пусть на этот объем V мы смотрим в момент времени t. Конф в мом. времени t обоз V(t). И наз. тек(актуальной ) конф-ей.

об. (в той же с-е)

(1) – Закон дв-ия

Ясно, что зависим. между и взаимноодн. (биекц) => => р-ва (1) могут быть разрешены отн-но

могу быть приняты за новую крив.ск. наз. матер. корд-ми. (корд-ы в мом. )

Траектории и линии тока:

Пусть заданы ск-ти т-к СС в пр-ой СК:

t-нефикс. Р-ая эту эту сис. как сис. дифф. ур-ий и помня, что при получим задачу Коши. Её реш-ие: - это закон дв-ия(6).

Зафикс в отч. конф. т-у , в (6) – корд-ты М. то р-во (6) предс. собой ур-ие какой-то линии в пр-ве:

Эта линия – геом. место т-к, в кот-х побывает т-а М. наз. траекторией. Закон дв-ия предс. собой траекторию.

Зафиксир. время t и построим поле ск-ей т-к СС. (в-ы ск-ти в каждой т-е) в поле проведем линии, касат. кот-х. в кажд. т-е. совп. с ск-тями: Линии, касат. кот-х в данный момент времени совп. со ск-тями наз. линиями тока.

2. Векторы скорости и ускорения

Пусть задан закон движения:

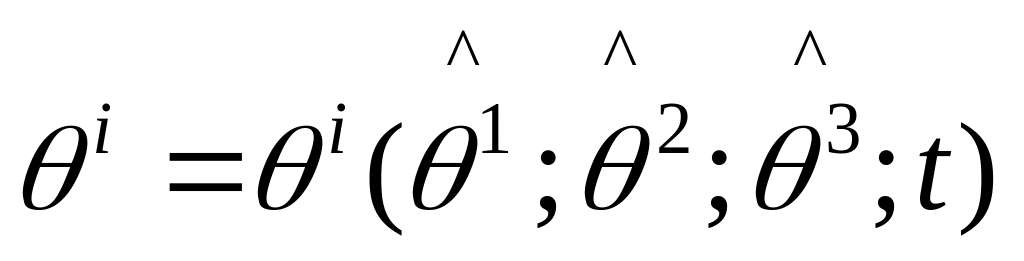
Радиус вектор произв. точки:

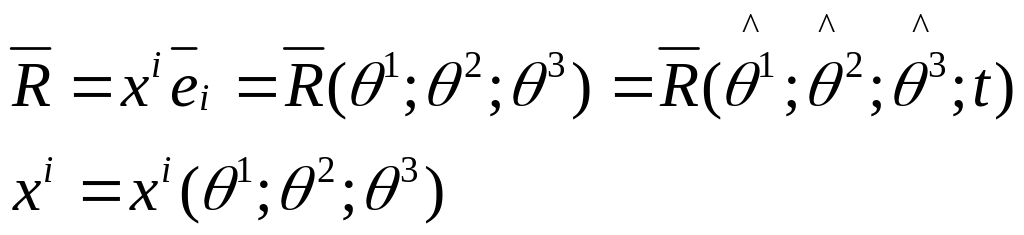
по определению скорость

Если независимые параметры ⁱ; t, то:

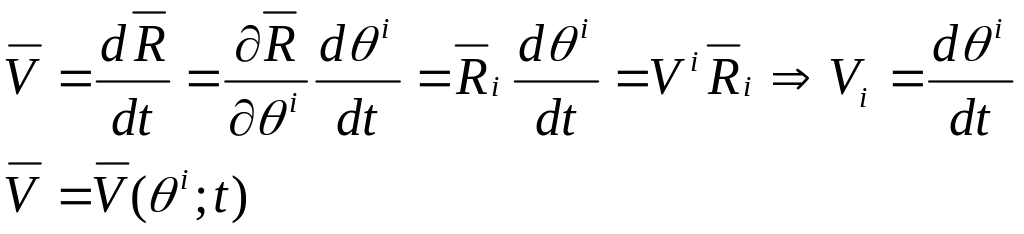
По определению ускорения:

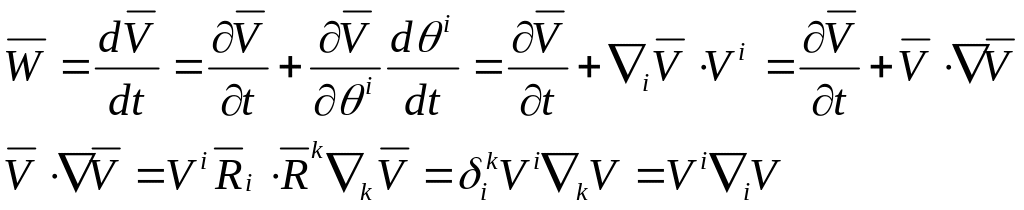
Если ⁱ; t, независимые:

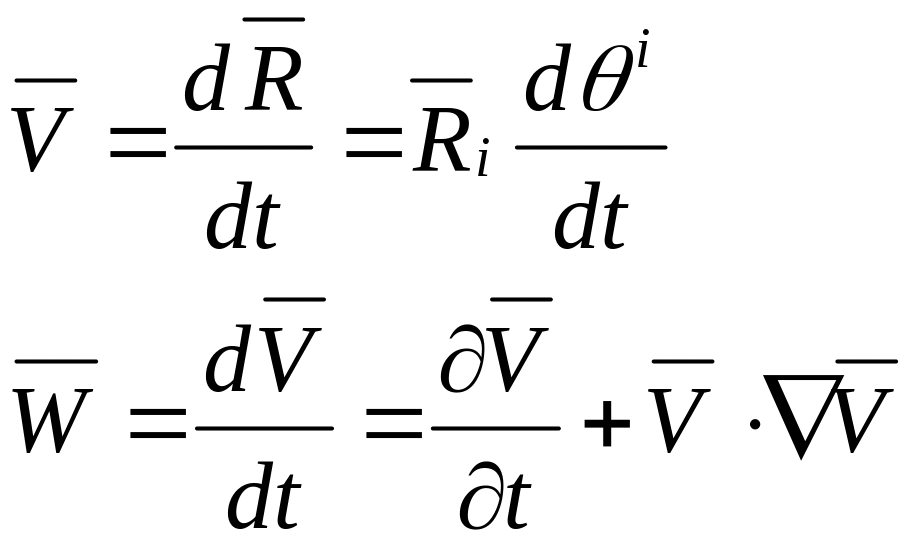
Вычислим в точке с корд (¹; ²; ³;) в момент времени t

3. Лагранжевый способ описания движения сплошной среды:

1. в качестве независ. корд-т рассмотрим.

т.е. все ф-ии через них выраж.

2.

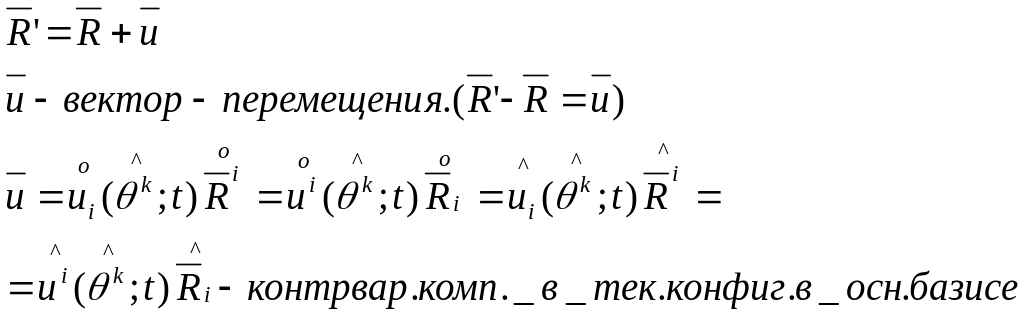Ск-ть:

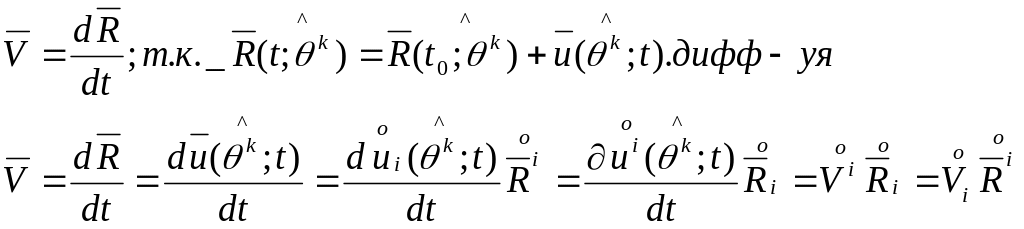В отчетном базисе:

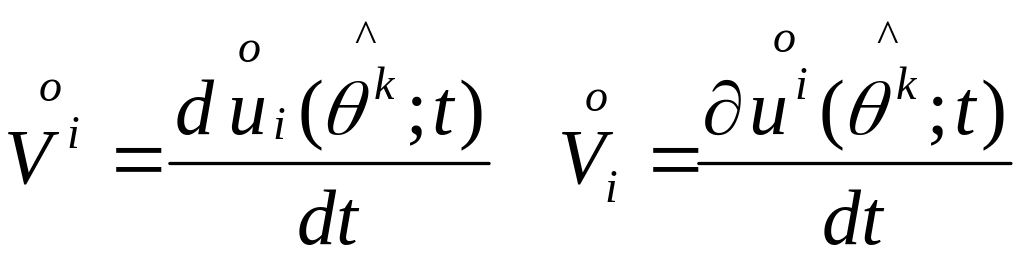
Уск-ие:

Аналогично получаем:

тех. конфигур.

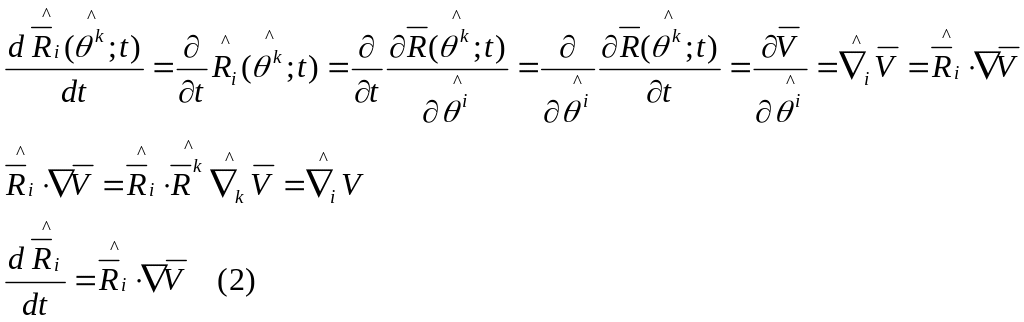продифф. По времени выр-ие: получим:

Рассмотрим ускорение:

Представим в-р V в тек. конф.

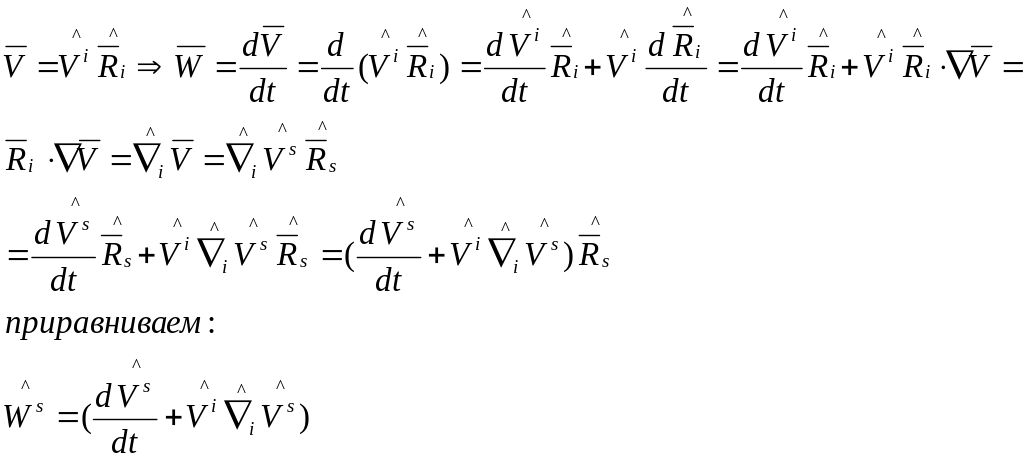Зная ф-и дифф-ия базисных векторов по времени можно найти корд. Скорости и ускорения в базисе.

т.к. способ Лагранжевый, то и материальные координаты называются Лагранжевыми.

Способ Эйлера

Движение описывается простр. Коор-ми:

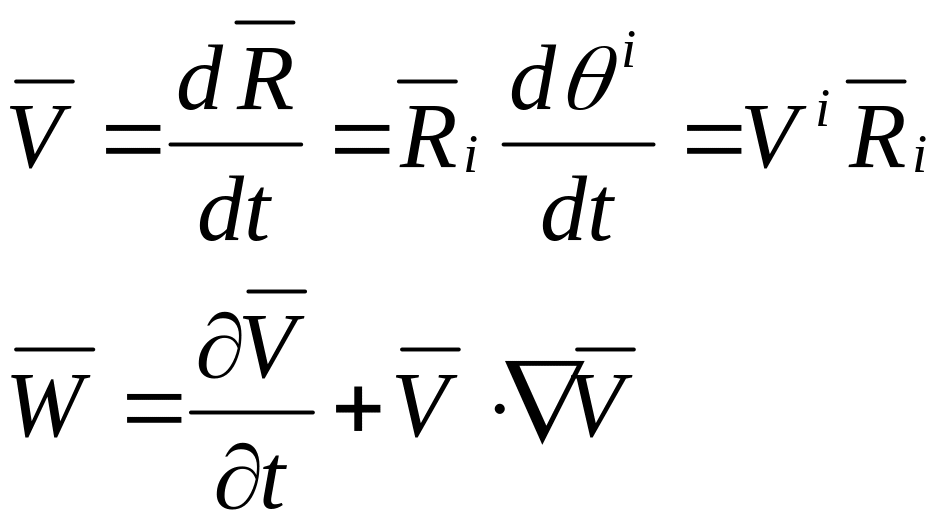
Пусть ск. ортонорм. и декарт. xⁱ; e_i

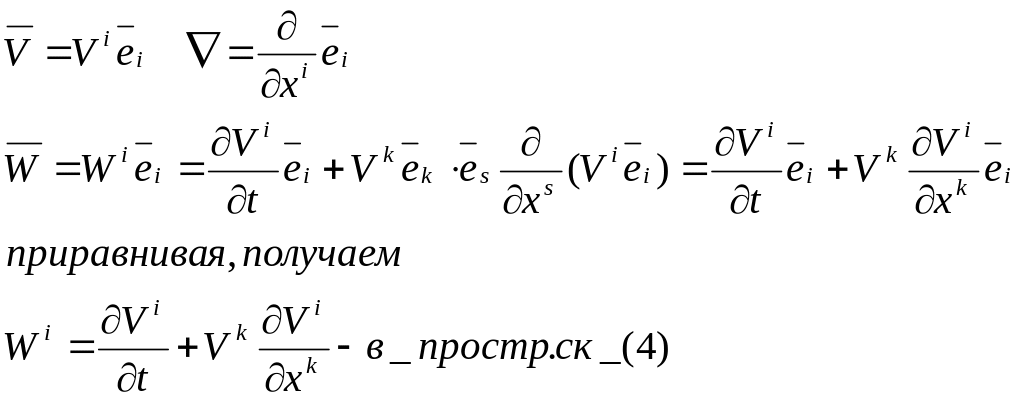
Эквивалентность способов Лагранжа и Эйлера описания дв-ия СС.

Описание движения СС способами Лагранжа и Эйлера

т.е. если известно описание движения Лагранжа, то можно получить Эйлера и на оборот.

Пусть задано описание движения СС способом Лагранжа

Поле ск-тей:

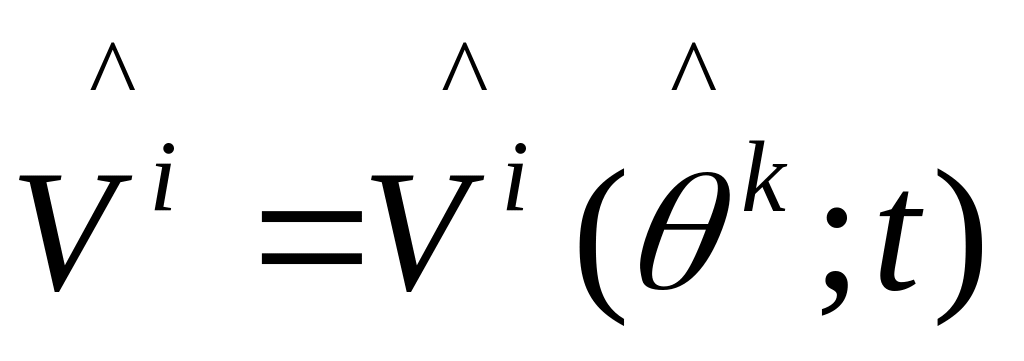
Ускорений:

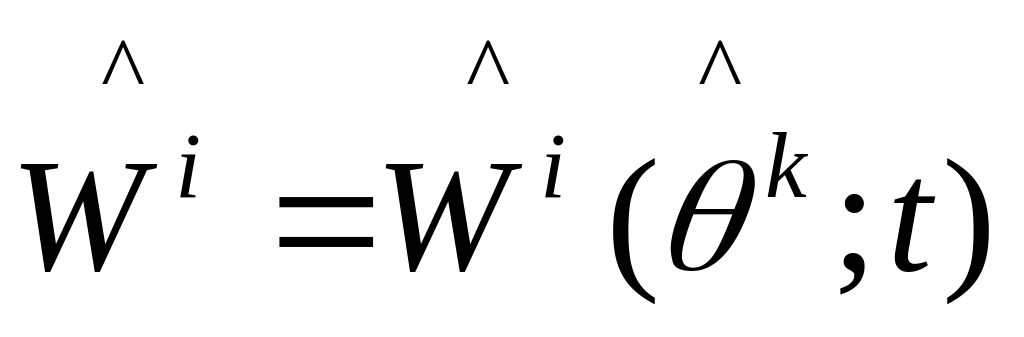
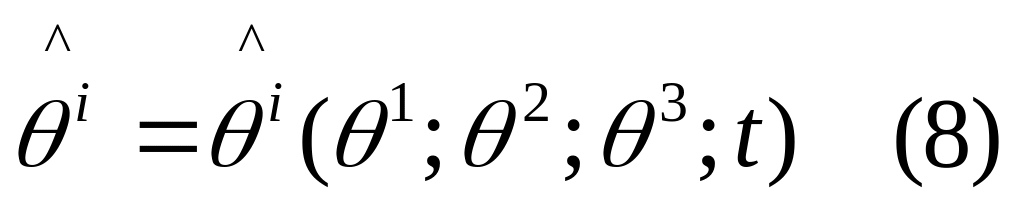
(8) можно р-ть, как ф-и пеорб-ия от и наоборот.

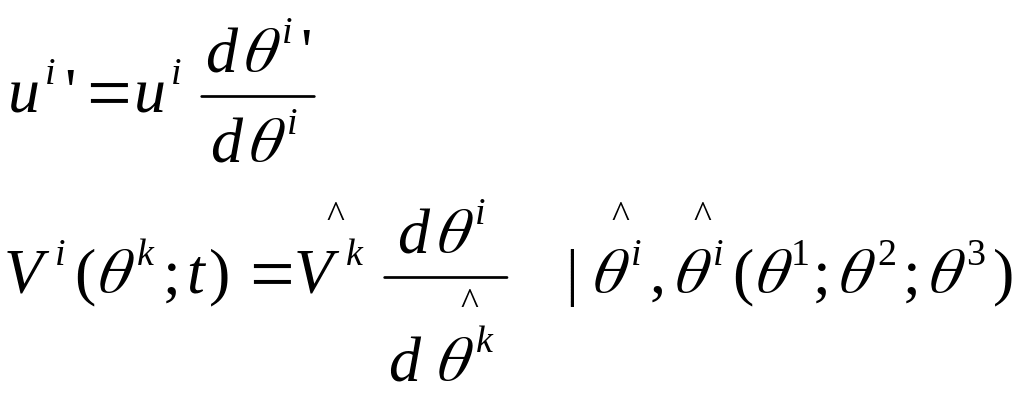
Пусть движение задано по Эйлеру:

Поле ск-тей:

Ее решение – закон движения

4. Движение бесконечно малого объема.

Связь между базисными векторами

Возьмем время t, тогда баз. векторы будут разл. Базисами в t=t_0;

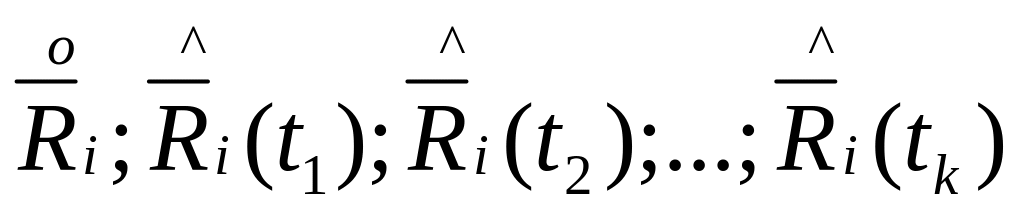
Введем в-р

продифф. По матер. Корд-м:

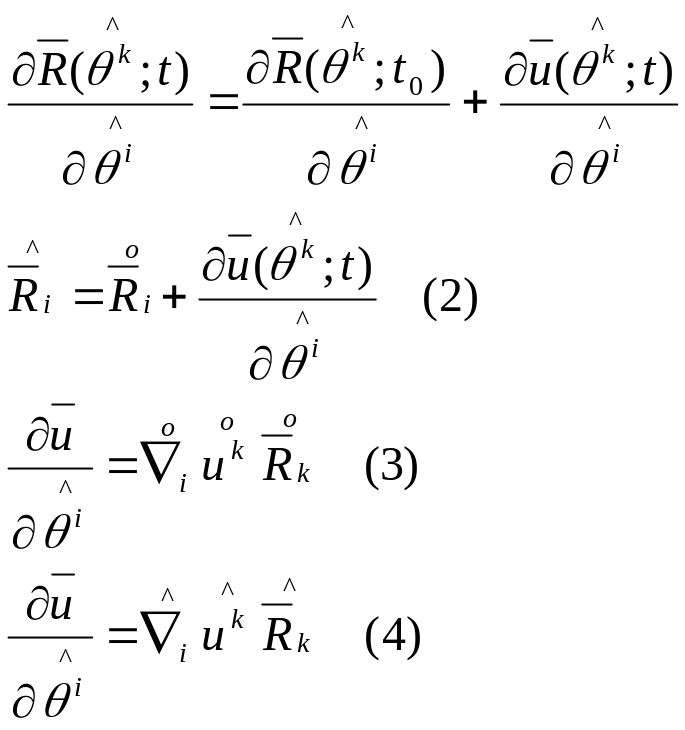
из (2) и (3) =>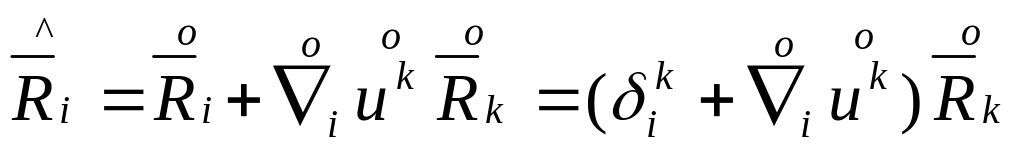

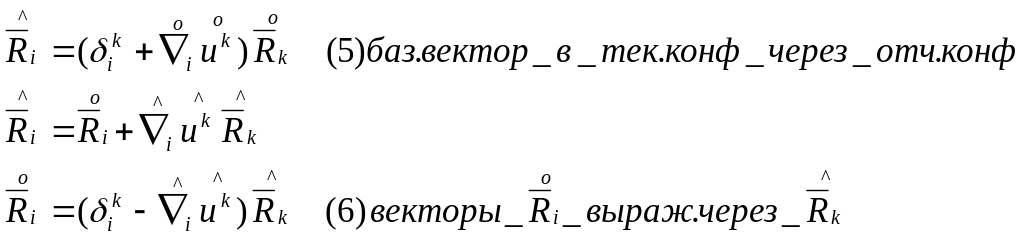
(5)и(6) – связь базисных в-ов в тек. и отч. Конф.

Р-м движение б.м. объема: пусть имеется точка с мат. корд.

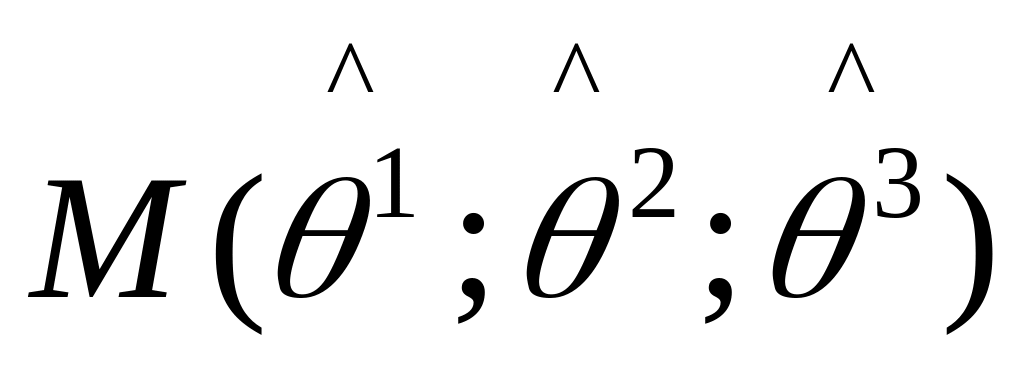и точка в окрестности М:

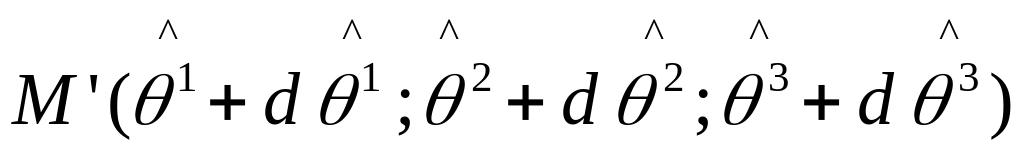
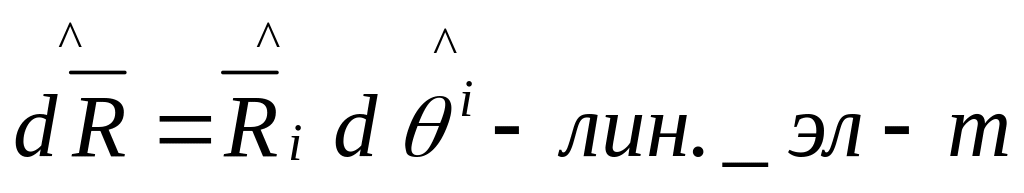
В мом. t=0 в отч. конф. точки М и М’ находились на расстоянии нек-го лин. эл-та:

В тек.

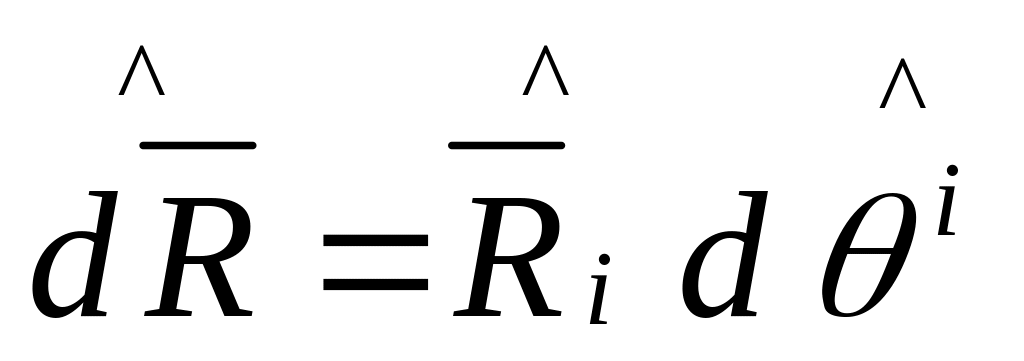
в-ы переходит приращение коорд. ( )одинак

t=0:

t=t

Все точки переходят в точки на

Введем тензор: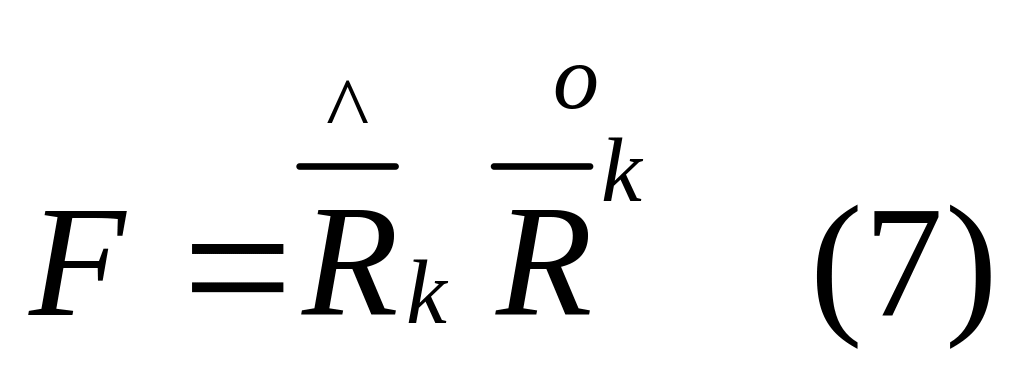

и вычисл:

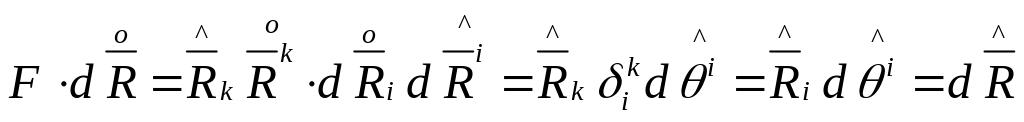
т.о. тензор F переводит эл-т в

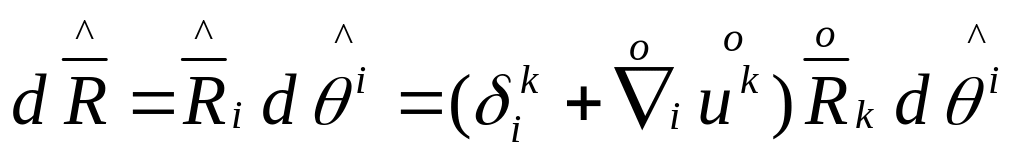
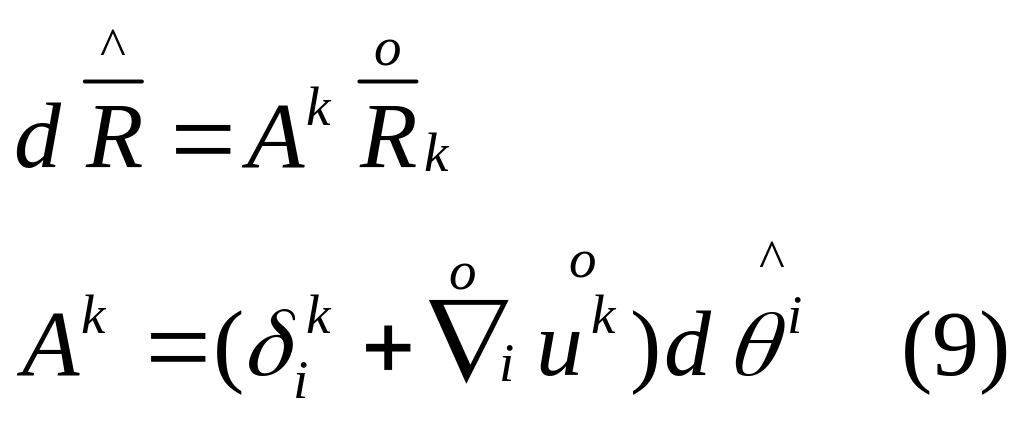
Из (8)и(9): в малой окр-ти точки М в процессе движения среды лин. эл-ты преобр. Друг в друга по лин. ф-ам. т.е. преобразование обьема происходит по лин. ф-лам (параллельные переходят в паралельные)