ЛЕКЦИЯ 5
Бинарные отношения. Основные определения
Глава 2. Отношения
Отношения - один из способов задания взаимосвязей между элементами множества. Наиболее изученными и чаще всего используемыми являются так называемые унарные и бинарные отношения.
(одноместные) Унарные отношения отражают наличие какого-то определенного признака R (свойства и т.п.) у элементов множества М (например, '‘быть белым шаром” на множестве шаров в урне). Тогда все такие элементы а из множества М, которые отличаются данным признаком R,
образуют некоторое подмножество в М, называемое унарным отношением R,
а R и R М
(двухместные) Бинарные отношения используются для определения каких-то взаимосвязей, которыми характеризуются пары элементов в множестве М
(на множестве людей заданы бинарные отношения:
“жить в одном городе”, “быть моложе”, “быть сыном”, “работать в одной организации” и т.п.).
Тогда все пары (а, b) элементов из М, между которыми имеет место данное отношение R, образуют подмножество пар из множества всех возможных пар элементов
М х М= М2,
называемое бинарным отношением R,
т.е. (a, b) R, при этом R M х М
В общем случае могут рассматриваться n-местные отношения,
например отношения
между тройками элементов - трехместные (тернарные) отношения и т.д.
Под n-местным отношением понимают подмножество R прямого произведения n множеств: n M1 x M2 x …x Mn.
Говорят, что элементы а1, а2, ..., аn (а1 M1, а2 M2 , ..., аn Mn) находятся в отношении R, если (а1, а2, ..., аn) R.
Если n-местное отношение R задано на множестве М своих элементов, т.е. M1 = M2 = …= Mn , то R Мn.
§ 2.1. Бинарные отношения. Основные определения
Двухместным, или бинарным, отношением R называется
подмножество пар (a, b) R
прямого произведения М1 х М2,
т.е. R M1 х М2. При этом
множество М1 называют областью определения отношения R,
множество М2 - областью значений.
Часто рассматривают
отношения R между парами элементов одного и того же множества М, тогда R М х М.
Если а, b находятся в отношении R записываем а R b.
|
Область определения D(R) |
область значений Q(R) |
D(R) = {а: (а, b) R} |
Q(R) = {b: (а, b) R} |
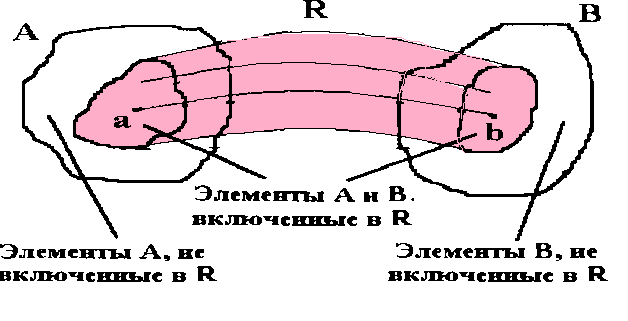
Пусть R A х B определено в соответствии с изображением на рис. 2.1.
Способы задания бинарных отношений
Бинарные отношения задаются
подмножествами множеств - прямых произведений.
Отношения |
определенные на конечных множествах |
задаются
|
Списком пар (перечислением) |
для которых это отношение выполняется |
R= {(а, b), (а, с), (b, d)} |
Матрицей бинарного отношения R М х М M =а1, а2, ..., аn |
соответствует квадратная матрица порядка n, в которой элемент сij , стоящий на пересечении строки i и столбца j, равен 1, если между ai и аj имеет место отношение R, или 0, если оно отсутствует |
|
|
|
|
|
|
|
|
|
|
Пример 1.
Пусть M = { 1, 2, 3, 4, 5, 6 }.
Задать в явном виде (списком) и матрицей отношение R M x М,
если R означает - “быть строго меньше”
Решение
Отношение R как множество содержит все пары элементов а, b из М такие, что а < b:
R = {(a, b): a, b М; а < b}
Тогда
R = {( 1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 5), (4, 6), (5, 6)}.
Матрица отношения Примеры 1, 2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
R a
b
1
2
3
4
5
6
a
b
1
2
3
4
5
6
a
b
1
2
3
4
5
6
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
2
0
0
1
1
1
1
2
0
1
0
1
0
1
2
0
1
0
1
0
1
3
0
0
0
1
1
1
3
0
0
1
0
0
1
3
0
0
1
0
0
1
4
0
0
0
0
1
1
4
0
0
0
1
0
0
4
0
1
0
1
0
1
5
0
0
0
0
0
1
5
0
0
0
0
1
0
5
0
0
0
0
1
0
6
0
0
0
0
0
0
6
0
0
0
0
0
1
6
0
1
1
1
0
1 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рис. 2.2 а) б) в) г) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 1. Условие Пусть M = { 1, 2, 3, 4, 5, 6 }. Задать в явном виде (списком) и матрицей отношение R M x М, если R означает - “быть строго меньше” Решение Отношение R как множество содержит все пары элементов а, b из М такие, что а < b: R = {(a, b): a, b М; а < b} Тогда
R = {( 1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 5), (4, 6), (5, 6)}. |
R = {(a, b): a, b М; а < b}
R
a
b
1
2
3
4
5
6
1
0
1
1
1
1
1
2
0
0
1
1
1
1
3
0
0
0
1
1
1
4
0
0
0
0
1
1
5
0
0
0
0
0
1
6
0
0
0
0
0
0 |
Пример 2. 1
Пусть М = { 1, 2, 3, 4, 5, 6 }.
Составить матрицы отношения R1, R2, R3 М х М,
если: 1) R1 - “быть делителем”;
2) R2 - “иметь общий делитель, отличный от единицы”;
3) R3 - “иметь один и тот же остаток от деления на 3”.
Решение
1) R1 = {(a, b) : а, b М; а – делитель b и
выполняется для пар
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (5, 5), (6, 6).
Пример 2. 1 Пусть М = { 1, 2, 3, 4, 5, 6 }. Составить матрицы отношения R1, R2, R3 М х М, если: 1) R1 - “быть делителем”; Решение R1 = {(a, b) : а, b М; а – делитель b и выполняется для пар (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (5, 5), (6, 6). |
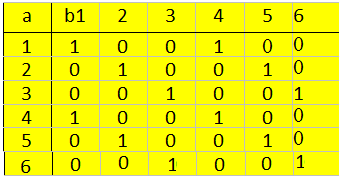
R1 = {(a, b) : а, b М; а – делитель b (a, b) R1 R1 M2 a, b M |
||||||||||||||||||||||||||||||||||||||||||||||||
a
b
b1
2
3
4
5
6
1
1
1
1
1
1
1
2
0
1
0
1
0
1
3
0
0
1
0
0
1
4
0
0
0
1
0
0
5
0
0
0
0
1
0
6
0
0
0
0
0
1 |
Эти пары (a, b) R1 определяют наличие единиц в матрице отношения R1 M2 на пересечении строки элемента а и столбца элемента b;
a, b M (рис 2.2,б)
Пример 2. 3
Пусть М = { 1, 2, 3, 4, 5, 6 }.
Составить матрицы отношения R1, R2, R3 М х М,
2) R2 = {(a, b) : а, b Î М; а и b имеют общий делитель, c 1}.
Решение
Матрица отношения R2 представлена на рис. 2.2, в;
Пример 2. 2 Пусть М = { 1, 2, 3, 4, 5, 6 }. Составить матрицы отношения R1, R2, R3 М х М, если: 2) R2 - “иметь общий делитель, отличный от единицы”; R2 ={(a, b) : а, b М; а – делитель с отличный от единицы R2 = (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 2), (4, 4), (4, 6), (5, 5), (6,2), (6, 3), (6,4), (6, 6) |
a |
b 1 |
2 |
3 |
4 |
5 |
6 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
1 |
0 |
1 |
0 |
1 |
|
3 |
0 |
0 |
1 |
0 |
0 |
1 |
|
4 |
0 |
1 |
0 |
1 |
0 |
1 |
|
5 |
0 |
0 |
0 |
0 |
1 |
0 |
|
6 |
0 |
1 |
1 |
1 |
0 |
1 |
|
R2 = {(a, b) : а, b Î М; а и b имеют общий делитель, c 1}. |
|||||||
Пример 2. 3
Пусть М = { 1, 2, 3, 4, 5, 6 }.
Составить матрицы отношения R1, R2, R3 Í М х М,
если:
3) R3 - “иметь один и тот же остаток от деления на 3”.
Решение
Пример 2. Пусть М = { 1, 2, 3, 4, 5, 6 }. Составить матрицы отношения R1, R2, R3 Í М х М, если: 3) R3 - “иметь один и тот же остаток от деления на 3”. Решение R3 = {(a, b): a,b М; а, b имеют один и тот же остаток от деления на 3}.
|
R3 ={(a, b) : а, b М; а –остаток r отличный от единицы R2 = (1, 1), (1, 4), (2, 2), (2, 5), (3, 3), (3, 6), (4, 1), (4, 4), (5, 2), (5, 5), (6, 3), (6, 6) |
Матрица отношения приведена на рис. 2.2, г.
Пример 3.
Для указанных ниже отношений привести примеры пар, для которых выполняются отношения, и пар, для которых отношения не выполняются.
Пример 3.
Для указанных ниже отношений привести примеры пар, для которых отношения не выполняются.
1. Отношения, заданные на множестве точек действительной плоскости: а) R1 - “находиться на одинаковом расстоянии от начала координат”; б) R2 -“находиться на разном расстоянии от начала координат”; в) R3- “находиться на одной и той же окружности с центром в начале координат”; г) R4 - “быть симметричным относительно оси X”. |
|
|
|
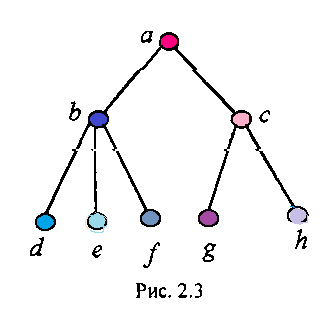
2. Отношения, заданные на множестве элементов структуры, изображенной на рис.2.3: а) R5 - “быть частью целого”; б) R6 - “быть непосредственно связанным с”, в) J?7 - “быть начальником”; г) Rg - “быть непосредственным начальником”.
|
|
||
