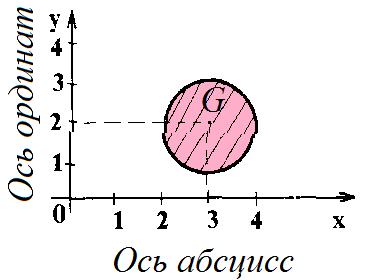- •Лекция № 8 - 11
- •Раздел 3 соответствия
- •Тема 3.1 Способы задания взаимосвязей
- •§ 3.1. Соответствия и их свойства. Основные определения
- •Упражнения
- •1. Соответствия g1- g8 определены графически на рис. 3.4.
- •2. Каковы свойства соответствия g между множеством n натуральных чисел и множеством м2n натуральных четных чисел:
- •§ 3.2. Функции и отображения
- •§ 3.3. Операции
- •Свойства бинарных операций:
- •Способы задания операций.
- •§ 3.4. Гомоморфизмы и изоморфизмы
Лекция № 8 - 11
Раздел 3 соответствия
Тема 3.1 Способы задания взаимосвязей
Соответствие - способ задания взаимосвязей и взаимодействий между элементами множества (наряду с отношениями R).
Частные случаи соответствий
функции
отображения
преобразования
операции ...
§ 3.1. Соответствия и их свойства. Основные определения
Соответствие между множествами А и В это
подмножество G прямого произведения этих множеств: G A х В.
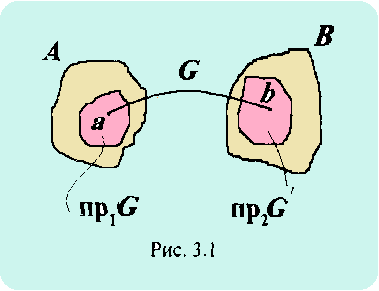
Если (а, b) G, то говорят, что “b соответствует а при соответствии G ”. Область определения соответствия G – множество np1 G = {а : (a, b) G}, Область значений соответствия G - множество пр2 G = {b : (а, b) G} (рис. 3.1). |
|
|
|
Свойства соответствий G A х В:
1 |
Всюду (полностью) определенное соответствие |
если np1 G = А |
Частично определенное соответствие |
в противном случае |
|
2 |
Сюрьективное соответствие Образом элемента а в множество В при соответствии G называется множество всех b В, соответствующих элементу а А.
Прообразом элемента b в множество А при соответствии G называется множество всех а Î А, которым соответствует b Î В.
Образом множества С np1 G называется объединение образов всех элементов а С.
Прообразом множества D пр2 G называется объединение прообразов всех элементов b D. |
если пр2 G = В |
3 |
Функциональное (однозначное) соответствие
|
если образом любого элемента а из области определения пр1 G является единственный элемент b из области значений пр2 G. |
4 |
Взаимно однозначное соответствие, если оно:
|
а) всюду определено; б) сюръективно; в) функционально; г) прообразом любого элемента b из области значений пр2 G является единственный элемент а из области определения пр1 G |
|
Если между множествами А и В существует взаимно однозначное соответствие, то мощности этих множеств равны |A| = |В| Говорят: если множества А и В равномощны, то можно
не вычисляя эти множества;
установив его взаимно однозначное соответствие с множеством, мощность которого известна или легко вычисляется. |
|
Множества, равномощные множеству натуральных чисел N - счетные.
Множества, равномощные множеству вещественных чисел R - континуальные.
Пример 1.
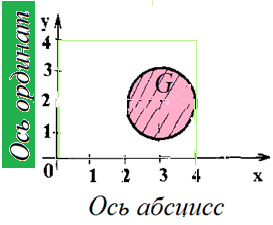
Пусть G - множество всех пар действительных чисел (х, у), удовлетворяющих соотношению (х-3)2+ +(у - 2)2 < 1.
Определить, чему равны:
а) образы и прообразы чисел 2, 3, 4;
б) образы и прообразы отрезков [2, 3], [2, 4].
Каковы свойства соответствия G?
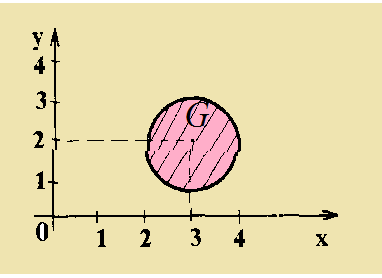
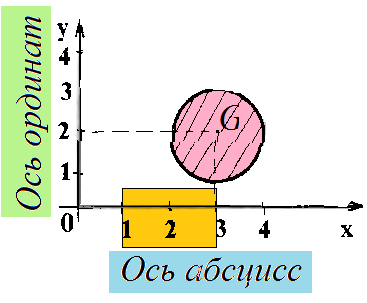
График соответствия G - круг радиуса 1 с центром в точке (3, 2). Таким образом, круг G задает соответствие между R и R (осью абсцисс и осью ординат, рис. 3.2).
|
Рис.3.2
|
Определить, чему равны: а.1) образы и прообразы чисел 2, а.2) образы и прообразы чисел 3, а.3) образы и прообразы чисел 4;
|
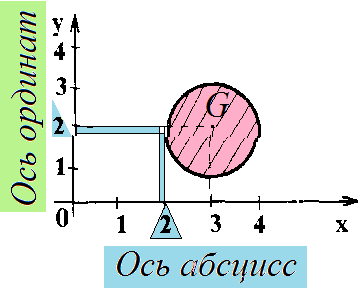
Решение а.1) Найдем сначала образы чисел Образом числа 2 пр1 G (на оси абсцисс) при соответствии G является единственное число 2 np2 G (на оси ординат).
|
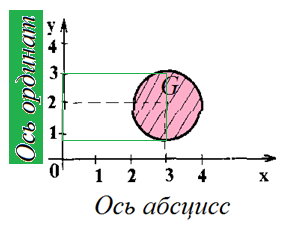
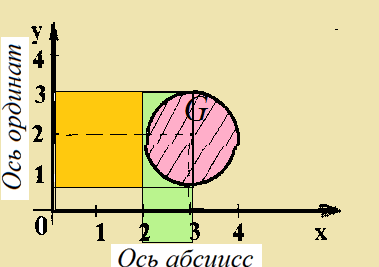
Решение а.2) Образ числа 3 при соответствии G есть множество всех действительных чисел отрезка [1, 3]
|
Решение а.2) образ числа 4
число 3 |
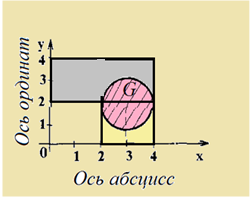
Решение а.1) Прообразом числа 2 пр2 G (на оси ординат) при соответствии G будет множество всех действительных чисел отрезка [2, 4] np1 G (на оси абсцисс)
|
|
Решение а.2) Прообразом числа 3 при соответствии G число 3
|
|
Решение а.3) Прообразом числа 4 при соответствии G не существует |
|
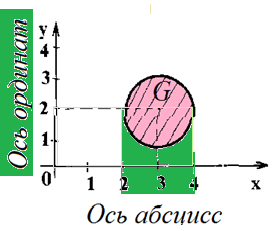
б) образы и прообразы отрезков [2, 3] Решение б) Образом множества чисел отрезка [2, 3] Í np1G является объединение образов всех чисел отрезка, т.е. отрезок [1, 3] np2G
|
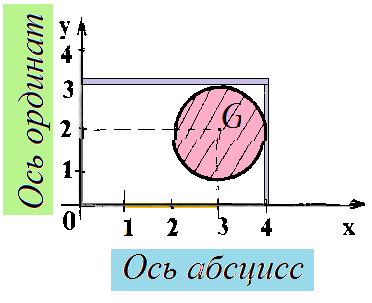
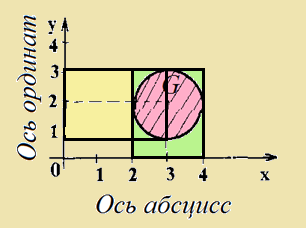
б) образы и прообразы отрезков [2, 3]. Решение Прообраз отрезка [2,3] при соответствии G - это отрезок [2, 4],
|
б) образы и прообразы отрезков [2, 4]. Образом отрезка [2,4] будет отрезок [1, 3] при соответствии G.
|
б) образы и прообразы отрезков [2, 4]. Решение Прообраз отрезка [2, 4] будет отрезок [2,4].
|
Каковы свойства соответствия G? Решение Если допустить, что соответствие G установлено на множестве действительных чисел, т.е. G R х R, то оно является:
Если определить соответствие G [2, 4] х [1, 3], то, оно будет всюду определенным и сюръективным, однако останется не функциональным и не взаимно однозначным.
|
|
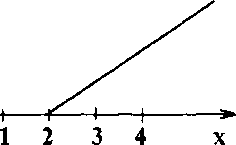 Пример
2.
Пример
2.
Пусть G - множество точек прямой линии, удовлетворяющей соотношению х-2= y => при y,x 0 (рис.3.3). Каковы свойства соответствия G?
|
Рис.3.3 |
Решение 1. Если соответствие G задано на множестве действительных чисел, т.е. G R х R, то G:
2. В случае, если соответствие G задано на множестве R + с нулем, т.е. G R + x R +, тогда соответствие G:
3. При G [2, ) х R + соответствие G:
|
|
Пример 3. Англо-русский словарь устанавливает соответствие между множествами английских и русских слов. Каковы свойства этого соответствия? Решение Данное соответствие не является:
|
|
Пример 4.
Пусть множества (U), где U= {а, b, с}, и В3 определены следующим образом:
(U), - множество всех подмножеств (булеан) множества U= {а, b, с};||
В3- множество всех двоичных векторов длины 3, т.е. В3 = А x А х А, где А={0, 1}.
Показать, что между множествами b(U), и В3 , где U= {а, b, с}, имеет место взаимно однозначное соответствие.
Решение b(U) ={, {а}, {b}, {с}, {а, b), {а, с}, {b, с}, {а, b, с}}; | b(U)| =8. В3= {(000), (001), (010), (011), (100), (101), (110), (111)}; |В3 | =8 (для упрощения обозначений мы опустим запятые между компонентами векторов ). Установим следующее соответствие G между множествами из b(U), и векторами из В3:
то в соответствующем ему векторе из В3 первая компонента равна 1, если отсутствует - то 0;
то в соответствующем ему векторе из В3 вторая компонента равна 1, если отсутствует - то 0;
Например, множеству {b} из b(U), соответствует вектор (010) из В3, множеству {а, с} - вектор (101) и т.д.: G: (000), {а} ® (100), {b} ® (010), {с} ® (001), {а, b] ® (110), {а, с} ® (101), {b, с} ® (011), {а, b, с} ® (111). ВЫВОД Очевидно, что установленное таким образом соответствие G является взаимно однозначным, так как выполняются все условия для взаимно однозначного соответствия. |
Пример 5.
Каковы свойства соответствия между множеством N натуральных чисел и множеством М2n степеней двойки:
G = {{n, 2n-1): n N, 2n-1 М2n N х М2n ?
Решение Соответствие G взаимно однозначно:
ибо для любого 2n-1 Î М2n существует единственное п N. |
Пример 6.
Используя определение равномощности множеств, показать, что множество М2n натуральных чисел, являющихся степенями двойки, счетно.
Решение Установим взаимно однозначное соответствие между множествами М2n и N. Если каждому натуральному n N поставить в соответствие число 2n-1 Î М2n, соответствие G N, очевидно, является взаимно однозначным (удовлетворяет всем требованиям для взаимно однозначного соответствия, см. пример 5) представляет множество всех векторов G = {(n, 2n-1): n ÎN. А так как мощность множества N счетна, то из установленной взаимной однозначности между множествами N и М2n согласно определению равномощности бесконечных множеств, следует, что множество М2n также счетно. |