Упражнения

1. Пусть X - множество {1, 2},

a Y - множество {х: х = =y+z; y,z ÎX}.

Определить в явном виде (списком) множе­ство Y.

Каковы множества ‘= {у: у = x+z; х, уÎХ}

и ‘‘ = {у: х= =y+z; х, zÎX} ?

2. Задать различными способами множество М₂„ всех чи­сел, являющихся степенями двойки: 2,4,8,16,..., не превы­шающих 300?

3. Задать различными способами множество натуральных чисел, кратных пяти: 5,10,15,20,...

4. Задать в явном виде (списком) множество (b(U)

всех под­множеств множества U, если U= {1, 2, 5, 7}. Какова мощ­ность множества b(U) ?

§1.2. Операции над множествами

Объединением множеств А и В (обо­значается А и В) называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств

А, В (рис 1.2):

А  В = {x: х Î А или х Î В}.

Пересечением множеств А и В (обозна­чается А  В) называется множество, со­стоящее из всех тех и только тех элемен­тов, которые принадлежат и А, и В (рис 1.3):

АÇ В = {х: хА и хВ}.

Объединение и пересечение произвольной совокупности множеств определяю гея аналогично. Символическая запись, например, для объединения: А È В È С È D;

; ; ; .

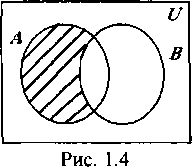
Разностью множеств А и В (обознача­ется А \ В) называется множество всех тех и только тех элементов А, которые не со­держатся в В (рис 1.4):

А\В= {х: хÎА и хÏВ}.

Разность - операция строго двухместная и некоммутатив­ная: в общем случае А \ В В \ А.

Рис. 1.5

Пусть U - универсальное множество такое, что все рассматриваемые множе­ства являются его подмножествами.

Дополнением (до U) множества А (обозначается А) называется множество всех элементов, не принадлежащих A (но принадлежащих U) (рис. 1.5):

= U\A.

Операции объединения, пересечения, дополнения {, , -} часто называют булевыми операциями над множествами.

Пример 1. Пусть универсальное множество U - множе­ство всех сотрудников некоторой фирмы; А - множество всех сотрудников данной организации старше 35 лет; В - множе­ство сотрудников, имеющих стаж работы более 10 лет,- С - множество менеджеров фирмы. Каков содержательный смысл (характеристическое свойство) каждого из следую­щих множеств:

а) ; б) Ç В ÇС; в) A È (B Ç ); г) В \ С; д) С \ В ?

Решение

а) - множество сотрудников организации, стаж ра­боты которых не превышает 10 лет.

Решение

б) Ç В Ç С- множество менеджеров фирмы не старше 35 лет, имеющих стаж работы более 10 лет.

Решение

в) A È (B Ç ) ­­- множество всех сотрудников фирмы стар­ше 35 лет, а также сотрудников, не являющихся менеджера­ми, стаж работы которых более 10 лет.

Решение

г) В\ С- множество сотрудников организации со стажем работы более 10 лет, не работающих менеджерами.

Решение

д) С \ В - множество менеджеров со стажем работы не более 10 лет.

Пример 2. Задать множества , , если:

М - множество всех натуральных чисел, не превосходя­щих 100;

N- множество натуральных чисел.

Решение

-множество всех натуральных чисел, больших 100.

Запись без контекста (т.е. без указания универсального множества U) не ясна:

• то ли это множество всех отрицательных целых чисел;

• то ли это множество положительных дробных чисел;

• то ли это пустое множество натуральных чисел.

Пример 3. Осуществить операции над множествами А = {а, b, с, d) и В = {с, d, e,f,g, h}.

Решение

А È В = {а, b, с, d, е, f g, h}; А Ç В = {с, d}.

Универсальное множество U не определено, поэтому, стро­го говоря, операции дополнения над множествами А и В не могут быть выполнены.

Дополним условие.

Пусть U ={а, b, с, d, е, f g, h),

тогда =U \ А = {е, f g, h},

={a, b}.

A\B = {a,b};

B\A = {e,f,g,h}.

Пример 4.

Пусть U= {1, 2, 3, 4},

А = {1, 3,4}, В= {2, 3},

С = {1, 4}.

Найти:

а) È ; б) ; в) А Ç ; г) (В \ А) È .

Решение а

а) È = (U \ А) È (U \ В) =

=({1, 2, 3, 4}\ {1, 3, 4}) È ({1, 2, 3, 4} \ {2, 3}) =

={2} È {1,4} = {1, 2,4}.

б) = U\ (А Ç В) = (1, 2, 3,4} \ ({1,3, 4} Ç {2, 3}) = ={1,2,3,4}\{3} = {1,2, 4}.

в) АÇ =A Ç (U\B)= {1,3,4} Ç ({1,2,3,4} \ {2,3}) = ={1,3,4}Ç{1, 4} = {1,4}.

Решение г

г) (В\А) È = ({2, 3} \ {1, 3, 4}) È ({1, 2, 3, 4} \ {1, 4}) = ={2} È {2,3} = {2,3}.