Теоретичні відомості:

1. Лінійна проста регресія є окремим випадком лінійної множинної регресії, коли k = 2. У цьому випадку в рівняння регресії, крім вільного члена а₀, якому відповідає допоміжна змінна х₀ (регресор) = 1, входить тільки одна дійсно пояснююча змінна, а саме, х₁ з регресійним коефіцієнтом а₁.

у = а₀ х₀+а₁х₁+е_t

2. Множинна регресія складається із двох простих регресій. При цьому:

а) перша регресія описується рівнянням, за умови відсутності х₂ –

у = а₀ х₀+а₁х₁+е_t.

б) друга проста регресія отримується, якщо відсутня х₁ –

у = а₀ х₀+а₂х₂+е_t.

Таким чином, трактування коефіцієнтів регресії зводиться до опису зміни залежної змінної – регресанда “у” під впливом регресора “х₀” (незалежної змінної) при зафіксованих значеннях інших змінних “х_k”.

3. Д 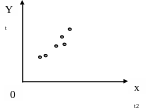іаграма розсіювання є зображення спостережень у площині даних змінних :

4. Процедуру побудови множинної регресії розглянемо на прикладі регресії з двома пояснюючими змінними. Функція лінійної множинної регресії в цьому випадку має вид:

(1)

Завдання полягає в оцінці параметрів регресії за результатами вибіркових спостережень над змінними, включеними в аналіз. Для цієї мети застосовуємо метод найменших квадратів. Поставимо умову, відповідно до якого регресія повинна по можливості добре узгоджуватися з емпіричними даними. Тому висунемо вимогу, по якому сума квадратів відхилень усіх значень, що спостерігаються, залежної змінної від значень, обчислених по рівнянню регресії (тобто сума квадратів залишків), повинна бути мінімальна. Отже, повинне виконуватися вимога:

,

Підставляючи замість y_i вираз (1), одержимо:

S є функцією від невідомих параметрів регресії. Необхідною умовою виконання служить обернення в нуль часткових похідних функції S (а₀,а₁,а₂) по кожному з параметрів а₀,а₁,а₂. Після відповідних алгебраїчних викладень одержуємо наступну систему нормальних рівнянь:

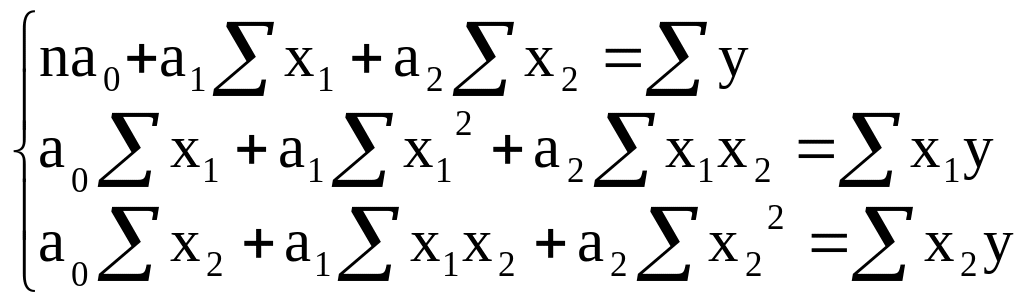
Розв’язавши дану систему рівнянь можна отримати значення коефіцієнтів: а₀, а₁, а₂.

5. На практиці крім звичайних оцінених регресійних коефіцієнтів оцінюються і інтерпретуються стандартизовані регресійні коефіцієнти. Вони відомі також під назвою "бета-коефіцієнти".

Оцінені значення стандартизованих регресійних коефіцієнтів можна обчислити за наступною формулою, яка одночасно може бути визначенням:

де – 1МНК-оцінка регресійного коефіцієнта а_і;

δ_хі - емпіричне стандартне (середньоквадратичне) відхилення і-го регресора х_і.

δ_y - емпіричне стандартне (середньоквадратичне) відхилення регресанда у.

Емпіричне стандартне відхилення допоміжної змінної х₀ для вільного члена дорівнює нулю, то = 0. Це означає, що немає сенсу розрахувати стандартизований вільний член.

Як інтерпретується стандартизований регресійний коефіцієнт? Перш за все передбачають, що емпіричні стандартизовані відхилення δ_хі і δ_y є типовими (характерними) змінами досліджуваних змінних. Тоді добуток δ_хі виражає типовий ефект впливу і-го регресора на регресанд. Чи буде цей ефект великим або малим, залежить від величини типової зміни регресанда.

6. Інтерпретація. Емпіричний стандартизований регресійний коефіцієнт вказує на те, наскільки є великим за інших рівних умов оцінюваний типовий ефект впливу і-го регресора в порівнянні з типовим ефектом зміни регресанда. Чим більша величина , тим більш значущим при інших рівних умовах є і-й регресор. Стандартизовані регресійні коефіцієнти визначаються при оцінці параметрів тоді, коли замість звичайних рядів спостережень використовуються стандартизовані ряди, наприклад, замість x_і.

7. Визначення коефіцієнтів еластичності.

При інтерпретації регресійних коефіцієнтів беруть до уваги одиниці виміру регресанда і регресорів. Для виявлення ступеню впливу регресора на регресанд без враховування одиниць виміру, крім регресійного коефіцієнта, можуть бути обчислені коефіцієнти еластичності (коротко: еластичність).

Еластичність регресанда y_t відносно регресора х_tk дорівнює:

де у* і х^*_і, - значення регресанда і і-го регресора, що визначають точку регресійної функції, для якої обчислюють коефіцієнт еластичності.

Еластичність є безрозмірним показником. Безрозмірність еластичності _k є перевагою: вона полегшує інтерпретацію.

В лінійному регресійному рівнянні часткова похідна ду/дх_і дорівнює регресійному коефіцієнту а_і. В цьому випадку істинна еластичність обчислюється:

Оцінена еластичність €k інтерпретується таким чином. Якщо за інших рівних умов і-й регресор зміниться на один відсоток, то регресанд внаслідок цього зміниться на €і відсотків.

Еластичність повністю формулюється так: "оцінена еластичність у відносно х_і (наприклад, оцінена еластичність попиту відносно доходів або оцінена еластичність товарообігу відносно торгової площі).

Контрольні питання:

1. Як отримується рівняння багатофакторної лінійної регресії.

2. Який економічний зміст багатофакторної регресії.

3. Як обчислити бета-коефіцієнти моделі і що вони характеризують.

4. Як обчислити коефіцієнт еластичності і який його економічний зміст.

5. Що характеризує діаграма розсіювання і як її побудувати.

МОДУЛЬ 2 "ЕКОНОМЕТРИЧНІ МЕТОДИ ТА МОДЕЛІ"

ЗМІСТОВНИЙ МОДУЛЬ 2 "БАГАТОФАКТОРНІ ЕКОНОМЕТРИЧНІ МОДЕЛІ ТА ВИПАДКИ ЇХ ОЦІНЮВАННЯ"