Приклади розрахунків характеристик динамічного і варіаційного рядів

Приклад розрахунку характеристик динамічного ряду

Розглянемо поквартальну заробітну плату (ЗП) у державному секторі України за 2002 — 2011 pp., грн. (таблиця 1.1).

Таблиця 1.1

№ п/п	Роки	ЗП у державному секторі (без ремій), тис. грн. — (Хі)
1	2002	115	12771.5	163111212
2	2003	238	12648.5	159984552
3	2004	362	12524.5	156863100
4	2005	761	12125.5	147027750
5	2006	1223	11663.5	136037232
6	2007	2220	10666.5	113774222
7	2008	6366	6520.5	42516920
8	2009	21224	8335.5	69513906
9	2010	42043	29156.5	850101492
10	2011	54313	41426.5	1716154902

Джерело: Тенденції української економіки / / Щомісячний бюле­тень 1 Європейський центр макроекономічного аналізу України. — 2011. — Серпень.

Проведемо підрахунки за цими даними й отримаємо такі середні характеристики.

Середня квартальна заробітна плата у державному секторі України в 2002 — 2011 pp. дорівнювала:

Середній абсолютний приріст заробітної плати дорівнює:

За середнім абсолютним приростом встановлено, що середній рівень заробітної плати щорічно на протязі досліджуваного періоду зростав на 6022 тис. грн.

Середні коефіцінти зростання та приросту відповідно становили:

Коефіцієнт зростання показує, що за досліджуваний період середнія заробітна плата за кожен рік зростала в 1,982 рази або на 1985,2%.

Дисперсія показує середню суму квадратів відхилень членів ряду від свого середнього і позначається ², або var(х_і):

де х — середнє значення динамічного ряду;

п — кількість спостережень.

Cереднє квадратичне відхилення дорівнює:

Коефіцієнт варіації за формулою:

де V — коефіцієнт варіації; х — середнє значення ряду;  — середнє квадратичне відхилення.

Для нашого прикладу дисперсія дорівнює: ²= 355508528.8; середнє квадратичне відхилення = 59624; коефіцієнт варіації V=426.68%.

Приклад розрахунку характеристик варіаційного ряду

При обстеженні студентів 1-го курсу за віком було зафіксовано такі дані: 17,18,18,18,18,19,20,20,20,21,21,21,21.

Позначимо частоту і-ї варіанти х_і через п тоді отримаємо ранжований дискретний варіаційний ряд. Дані для розрахунків наведені у табл.1.2.

Таблиця 1.2.

Номер варіанти	Значення варіанти Хі	Частота варіанти n
1	17	1	-2,38	5,66	5,66
2	18	4	-1,38	1,90	7,61
3	19	1	-0,38	0,14	0,14
4	20	3	0,62	0,38	1,15
5	21	4	1,62	2,62	10,49

Для дискретного варіаційного ряду середня арифметична розраховується за формулою:

де х — середня арифметична; х_і — і-та варіанта; п — частота і-ї варіанти.

Медіаною називається таке значення ознаки, що вивчається, яке припадає на середину варіаційного ряду. При знаходженні медіани можливі два випадки: кількість членів ряду парна (d = 2k) та непарна (d = 2k+1).

У другому випадку медіана дорівнює:

де M — медіана; х_k+1 — значення (k+1)-го члена варіаційного ряду. У першому випадку:

де M_е — медіана; х_к, х_к+1 — відповідно k та (k + 1) варіанти.

Модою називається варіанта, яка найчастіше зустрічається в даному варіаційному ряду.

Характеризує розсіяння навколо середнього – дисперсія ( ):

Якщо дисперсію зручно подавати в тих самих одиницях виміру, що й варіанти, то використовують середнє квадратичне відхилення ():

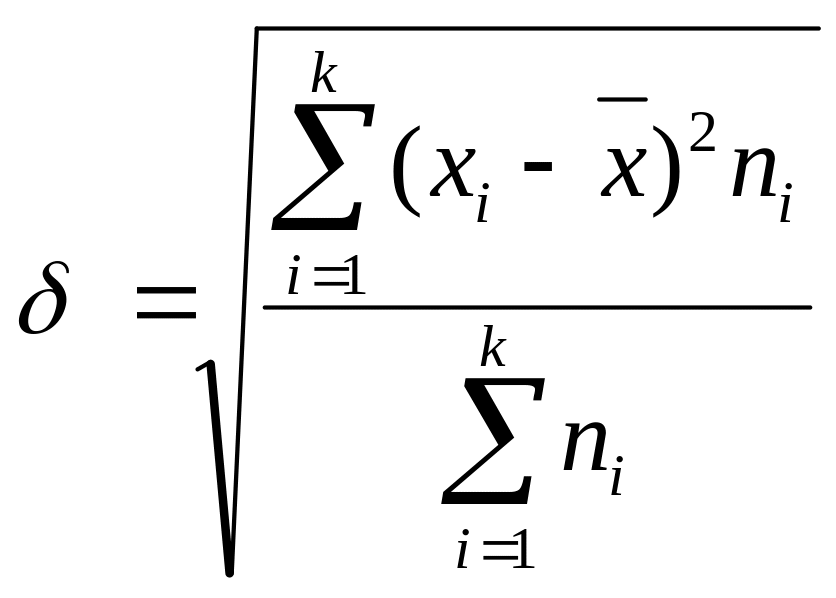
Для варіаційних рядів розраховується також коефіцієнт варіації (V):

Середній вік студентів 1-го курсу дорівнює: х = 19,38. Медіана відповідно дорівнює:

а мода:

Дисперсія варіаційного ряду =l.927, середнє квадратичне відхилення = 1,38, а варіація V = 7.16%.