Теоретичні відомості

Природа автокореляції.

Одним із припущень класичного регресійного аналізу є припущення про незалежність випадкових величин. Якщо це припущення порушується, то ми маємо справу з автокореляцією. В регресійній моделі автокореляція наявна у разі, коли випадкові величини залежні між собою, тобто:

.

Потрібно розрізняти поняття автокореляції і серійної кореляції. Автокореляцією називається залежність між значеннями однієї вибірки з запізненням в один лаг. Автокореляція може бути як позитивною, так і негативною. Автокореляція може виникнути у зв’язку з інерційністю та циклічністю багатьох економічних процесів. Провокувати автокореляцію може і неправильно специфікована функціональна залежність у регресійних моделях та лагові запізнення в економічних процесах.

Тестування автокореляції

Найбільш відомим і поширеним тестом перевірки моделі на наявність кореляції між залишками є тест Дарбіна-Уотсона. На відміну від багатьох інших тестів, перевірка за тестом Дарбіна-Уотсона складається з декількох етапів і включає зони невизначеності.

Розглянемо порядок тестування за критерієм Дарбіна-Уотсона.

1. На першому етапі розраховується значення -статистики за формулою (1):

(1)

У теорії доведено, що значення -статистики Дарбіна-Уотсона знаходяться в межах від 0 до 4.

2. Задаємо рівень значимості та підраховуємо кількість факторів у досліджуваній моделі. Припустимо . За таблицею Дарбіна - Уотсона при заданому рівні значимості , кількості факторів та кількості спостережень п, знаходимо два значення та . Якщо розраховане значення -статистики знаходиться в проміжку від 0 до 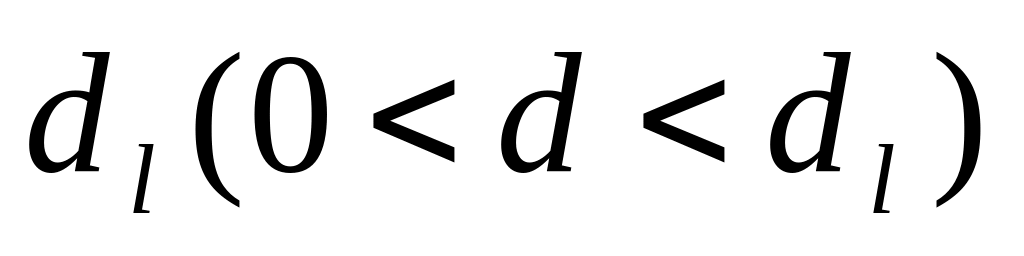, то це свідчить про наявність позитивної автокореляції. Якщо значення потрапляє в зону невизначеності, тобто набуває значення , або , то ми не можемо зробити висновки ні про наявність, ні про відсутність автокореляції. 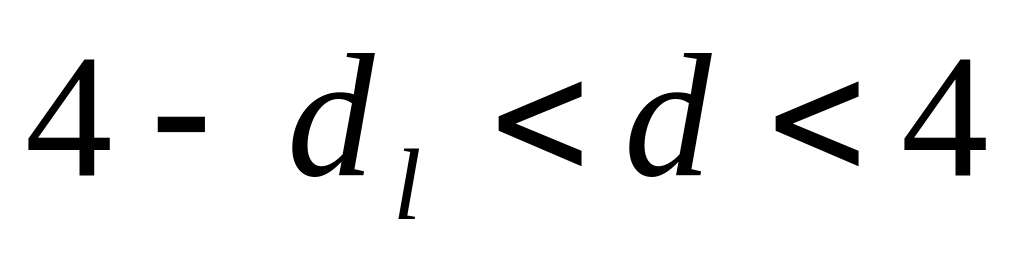Якщо , то маємо негативну автокореляцію. Нарешті, якщо , то автокореляції немає.

Приклад. Припустимо, для певної простої регресійної моделі, яка має один фактор , кількість спостережень дорівнює та розраховане значення -статистики дорівнює 0,34. Приймемо, що рівень значимості, тобто ризик відкинути правильну гіпотезу, дорівнює 5%. За таблицею Дарбіна-Уотсона при та знаходимо 1,20; 1,41. Відповідно відкидаємо гіпотезу про відсутність автокореляції та приймаємо гіпотезу про наявність позитивної автокореляції.

Оцінка параметрів регресійної моделі при наявності автокореляції

Розглянемо просту лінійну регресійну модель:

(2)

Припустимо, що всі класичні припущення виконуються, крім припущення про незалежність випадкових величин, тобто:

Припустимо також, що між випадковими величинами є лінійна залежність:

(3)

де — коефіцієнт автокореляції; — випадкова величина, для якої використовуються всі класичні припущення методу найменших квадратів:

(4 )

Модель (4) відома лід назвою авторегресивна модель Маркова першого порядку (АR(1)), або авторегресивна лагова. У такій інтерпретації коефіцієнт автоковаріації називається коефіцієнтом автокореляції першого порядку, або коефіцієнтом автокореляції з лагом 1.

Отже, для того, щоб дослідити вплив автокореляції на оцінку невідомих параметрів, повернемось до моделі (2). Розглянемо для спрощення тільки оцінку параметра , яка за методом найменших квадратів знаходиться за формулою 5:

(5)

Дисперсія параметра при відсутності автокореляції дорівнює:

(6)

За наявності автокореляції, наприклад типу АR(1), дисперсія параметра змінює своє значення (доведення цього факту ми не наводимо);

(7)

Якщо , то обидві формули будуть однаковими, але при наявності автокореляції дисперсія параметра відрізнятиметься від значення дисперсії за відсутності автокореляції.