Приклад виконання роботи

Отримано набір статистичних даних, що характеризують залежність прибутку підприємства (у, тис.грн.) від виробничих витрат (х₁, тис.грн.) і середньорічних залишків запасів (х₂, тис.грн.) та середньої кількості працівників (х₃, чол.). Перевірити на наявність мультиколінераності залежність у = f(x₁,x₂,х₃) і знайти методи її усунення.

Таблиця з вхідними даними

Прибуток підприємства (у, тис.грн.)	Виробничі витрати (х1, тис.грн.)	Середньорічні залишки запасів (х2, тис.грн	Середня кількость працівників (x3, чол.).
4,2	6,9	6	200
1,5	2,9	5,4	210
2,8	3,5	3,1	230
5,6	9,1	7,2	200
2,5	5,2	4,6	250
3,9	6,5	3,9	240
3,8	2,9	3,8	205
4,6	1,4	2,6	210
4,9	8,8	6,8	230
7,2	11,5	8,5	210
5,3	4,9	1,8	200

1. Знайдемо часткові коефіцієнти кореляції r_yx1, r_yx2, r_{yx3 ,} r_x1x2, r_x1x3, r_x2x3. і побудуємо кореляційну матрицю.

Побудуємо кореляційну матрицю використовуючи настройку “Аналіз даних – Кореляція” електронної таблиці Excel.

Кореляційна матриця матиме вигляд (табл.2).

Таблиця 2

Кореляційна матриця економічних показників

	y	x1	x2	x3
y	1
x1	0,690433	1
x2	0,404724	0,819116	1
x3	-0,40934	-0,01483	-0,0979	1

Після аналізу кореляційної матриці можна зробити висновок, що коефіцієнти х₁ і х₂ мають велике значення коефіцієнту кореляції і це може свідчити про наявність лінійної залежності між ними. На основі даного висновку можна говорити про наявність мультиколінеарності в даній моделі.

2. Визначимо ступінь колінеарності. У разі відсутності мульти­колінеарності у моделі множинний коефіцієнт детермінації R²_yx1x2х3 буде приблизно дорівнювати сумі часткових коефіцієнтів детермінації R²_yx1, R²_yx2, R²_yx3. Якщо мультиколенеарність присутня, тоді це рівняння виконуватись не буде і у якості виміру мультиколінеарності можна використати змінну М₁:

М₁ = R²_yx1x2x3 – ( R²_yx1 + R²_yx2 +R²_yx3 ).

Чим більше змінна М₁ наближатиметься до нуля, тим менша мультиколінеарність.

Знайдемо коефіцієнти детермінації. Для цього використовуємо надстройку “Аналіз даних– Регресія”.

R²_{yx1x2x3 =} 0,754283 (будуємо регресі ю між y та x₁, x₂, x₃)

R²_yx1= 0,476698 (будуємо регресі ю між y та x₁)

R²_yx2= 0,163801 (будуємо регресі ю між y та x₂)

R²_yx3= 0,167558 (будуємо регресі ю між y та x₃)

M₁= 0,754283 – 0,476698 – 0,163801 – 0,167558= – 0,053774

Відповідно, до нашого приклада: М₁ ненаближається до 0, тому слід вважати наявність мультиколінеарності.

3. Перевіримо інтенсивність мультиколінеарності за формулою:

Відповідно до нашого приклада отримаємо:

Даний коефіцієнт значно більший нуля, тому можна говорити про високу інтенсивність мультиколінеарності.

4. Одним із методів усунення мультиколінеарності є метод виключення змінних за Фарраром та Глаубером.

Процедура відбору змінних складається з трьох кроків. При цьому передбачається нормальне розподілення залишків.

Крок 1. Мультиколінеарність виявляється в загальному вигляді. Для цього будується матриця R коефіцієнтів парної кореляції між пояснюючими змінними та визначається її визначник.

r_ij=cov(x_i, x_j)/σ_xi σ_xj

Кореляційну матрицю можна отримати використовуючи пакет “Аналіз даних” електронної таблиці Excel інструмент “Кореляція”.

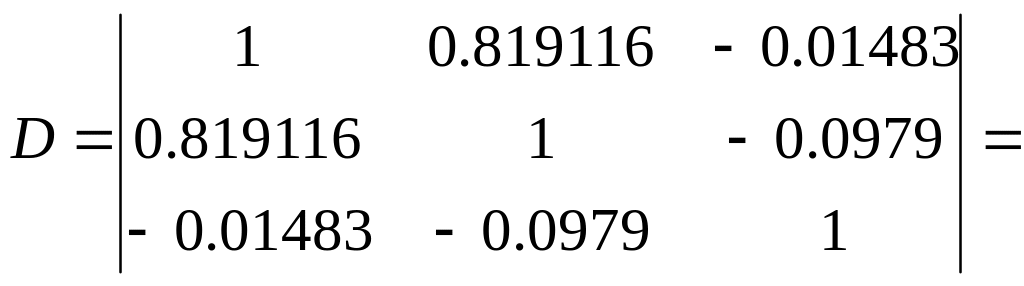0,321622

Далі для перевірки наявності мульколінеарності взагалі серед пояснюючих змінних використовується хі квадрат критерій χ² (хі квадрат ).

Висувається нульова гіпотеза Н₀: між пояснюючими змінними мультиколінеарність відсутня. Альтернативна гіпотеза Н₁:між пояснюючими змінними є мультиколінеарність.

Розраховують значення χ²

χ²= – (n-1-1/6*(2*m+5))*lnD

де n–кількість спостережень, m– кількість пояснюючих змінних.

Ця величина має розподіл χ² з f=1/2*m*(m-1) ступенями вільності. Якщо розраховане значення χ² менше за табличне, то Н₀ приймається_. вважаємо, що мультиколінеарності між пояснюючими змінними немає. Інакше, визначають данні які сильно корелюють визначається на другому кроці.

χ²= – (10-1-1/6*(2*3+5))*ln(0,321622)=8,1297,

f=1/2*3*(3-1)=3.

Табличне значення χ²= 7,815 (при f=3 та α=0,05)

Таким чином (8,1297 ≥ 7,815), тому гіпотеза про наявність мультиколінеарності між пояснюючими змінним не суперечить даним дослідження

Крок 2. Використовуються коефіцієнти детермінації між пояснюючими змінними R²k12…k-1k+1…m. Оцінка мультиколінеарності основана на тому, що величина

має F-розподіл з f₁=m-1 I f₂=n-m ступенями вільності.

Якщо F≥F_α;f1,f2, то змінній x_k в найбільшому ступені притаманна мультиколінеарність. По Фаррару і Глауберу вивчення m значень F-статистик має показувати, які з пояснюючих змінних в більшій мірі підверджені мультиколінеарності.

R² _x1,x2,x3 = 0,675265

F = (10-2)*0,675265/[(2-1)*(1–0,675265)]= 16,6355

F ≥ F_табл.

R² _x2,x1,x3= 0,678307

F = (10-2)*0,678307/((2-1)*(1-0,678307))= 16,8684

F ≥ F_табл.

R² _x3,x1,x2= 0,02257

F = (10-2)*0,02257/((2-1)*(1–0,02257))=5,367608/0,329049=0,18473

F < F_табл.

F_{табл .}= 5,32 з f₁ = m-1 = 2-1 = 1 I f₂ = n-m = 10-2=8 ступенями вільності.

F ≥ F_табл.

Таким чином змінним х₁ та х₂ в найбільшому ступені притаманна мультиколінеарність

Крок 3. З’ясовується, яка пояснююча змінна породжує мультиколінеарність, та вирішується питання про її виключення з аналізу. Для цієї цілі розраховується коефіцієнт частинної кореляції r_jk12…m (j, k=1,2,…,m; j <> k) між пояснюючими змінними. Змінна y в розрахунок не береться. В якості критерію використовується величина

що має t-розподіл з f = n – m ступенями вільності. Якщо t_j,k > t_α,f, то між змінними існує колінеарність и одна з них має бути виключеною. При виключенні змінної дослідник має опиратися як на власну інтуїцію, та і на змістовну теорію явища. Якщо t_j,k ≤ t_α,f, то дані не підтверджують наявність колінеарності між змінними x_j та x_k .

Знайдемо коефіцієнти частинної кореляції r_jk12…m (j, k=1,2,…,m; j<>k) між пояснюючими змінними. Кореляційна матриця має вигляд.

	x1	x2	x3
x1	1
x2	0,819116	1
x3	-0,01483	-0,0979	1

t_0.05;8 = 2,31

r² ₁₂₃ = r² ₁₂+r²₁₃,

r² ₂₃₁ = r² ₂₃+r² ₂₁

r² ₃₁₂ = r² ₃₁+r²₃₂

1. r² ₁₂₃

r² ₁₂₃ = 0,819116²+(–0,01483)² = 0,671171, r ₁₂₃ = 0,819225

4.040761

t₁₂ > t_0.05;8 Між змінними х₁ та х₂ існує колінеарність.

2. r² ₂₁₃

r² ₂₃₁ = (–0,0979)² + 0,819116² = 0,68053, r ₂₁₃ = 0,824946

4.12815

t₂₃ > t_{0.05;8 .} Між змінними х₂ та х₃ існує колінеарність.

3. r2 ₃₁₂

r² ₃₁₂ = (–0,01483)²+(–0,0979)² = 0,009804 = 0,099017

0,281445

t₃₁ < t_0.05;8. Між змінними х₃ та х₁ не існує колінеарність.

Висновок: змінну х₂ потрібно вилучити з розгляду. Наша модель буде показувати залежність між y (прибутку підприємства, тис.грн.) та х₁ (виробничих витрат, тис.грн.) та х₃ (середньої кількості працівників, чол.).

Економетрична модель буде мати вигляд:

y = 9,976384 + 0,349471*x₁ – 0,03592*x₂

Контрольні питання:

1. Поняття мультиколінеарності.

2. Причини виникнення мультиколінеарності.

3. Тестування наявності мультиколінеарності.

4. Методи усунення мультиколінеарності.

Лабораторна робота № 7

(2 години)

Тема: “Гетероскедастичність у багатофакторному регресійному аналізі"

Мета роботи: Дослідити поняття гетероскедастичності та гомоскедастичності. Освоїти методики оцінки особливих випадків багатофакторного регресійного аналізу із допущенням гетероскедастичності.

Теоретичні відомості.

Одним з основних припущень моделі класичної лінійної регресії є при­пущення про сталість дисперсії кожної випадкової величини е. (гомоскедастичність). Формалізовано це припущення записується у вигляді:

Якщо це припущення не задовольняється у якомусь окремому випад­ку, то має місце гетероскедастичність:

Суть припущення гомоскедастичності полягає в тому, що варіація кож­ної e_t навколо її математичного сподівання не залежить від значення х. Дисперсія кожної e_i. зберігається сталою незалежно від малих чи вели­ких значень факторів: σ²e не є функцією x_ij тобто σ²e<> f(x1i, x_2i,...,x_pi ). Якщо σ²e не є сталою, а її значення залежать від значень х, можемо записати У цьому разі маємо справу з гетероскедастичністю.

Наслідками порушення умови гомоскедастичність є: неможливість перевірки значимості параметрів регресії та побудови інтервалів довіри (дисперсія випадкової величини не стала, а змінюється), якщо вони отримані за методом найменших квадратів:

;

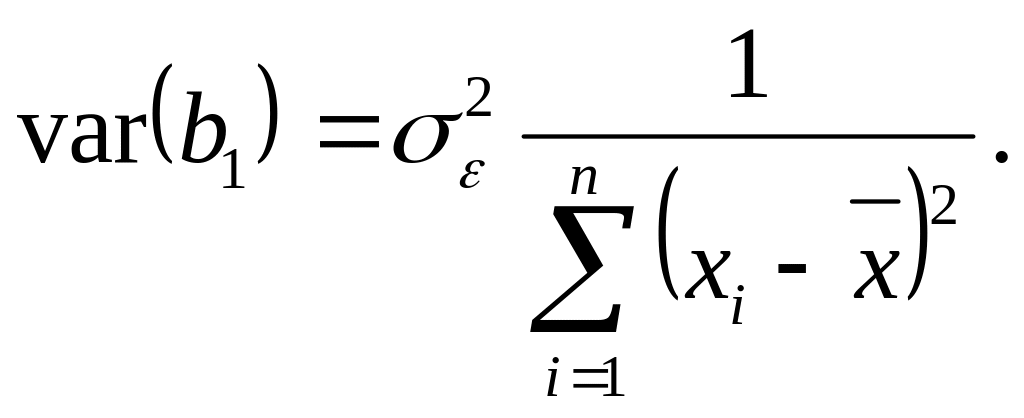
і таким чином, оцінки параметрів регресії втрачають таку перевагу над іншими оцінками, як те, що вони мали найменшу дисперсію. Тому оцінки параметрів доцільно знаходити за узагальненим методом найменших квадратів (інша назва – метод Ейткена)

Методи визначення гетероскедастичності .Єдиних правил виявлення гетероскедастичності не­має, а є різноманітні тести.

1. Графічний аналіз. Суть методу у наступному:

а) Побудувати багатофакторну регресійну модель з припущенням про про відсутність гетероскедастичності.

б) намалювати графік зележності відхилень моделі і фактору у і з’ясувати, чи мають вони якусь систематичність.

в) намалювати графік зележності відхилень моделі і фактору х з’ясувати, чи мають вони якусь систематичність.

г) зробити висновок про саму форму зв’язку, що особливо корисно при трансформації наявних даних для побудови моделі з гомоскедастичністю помилок.

2. Тест рангової кореляції Спірмена. Алгоритм методу:

а) Представити модель у вигляді рівняння регресії: y_i=β₀ +β₁x_i+β₂x₂+ε_i.

б) На основі регресії розрахувати відхилен­ня е_i .

в) Взявши абсолютні значення | е_i |, ранжуємо |e_i | та у_i у зростаючому чи спадному порядку і підрахувати ко­ефіцієнт рангової кореляції Спірмена для всіх пар |e_i | та у_i за формулою:

де d — різниця між рангами, що приписуються двом характеристикам і-го об'єкта;

n — кількість об'єктів, що ранжуються.

г) Перевірити значимість отриманого коефіцієнта рангової ко­реляції за f-критерієм Ст'юдента. Для цього побудувати t-статистику:

де n — кількість спостережень;

= (n - 2) — кількість ступенів вільності.

При даних ступенях вільності за таблицями Ст'юдента знайти t. Якщо розраховане значення перевищує t_кр (t > t_кр ), це підтверджує гіпотезу про гетероскедастичність. Якщо t ≤ t_кр , тоді в регресійній моделі правильним є припущення про гомоскедастичність.

3. Тест Глейзера. Алгоритм методу:

а) Знайти невідомі параметри лінійної регресії методом найменших квадратів та обчислити помилки e_і для кожного окремого спостереження.

б) Побудувати регресію е = f(у), яка пов'язує абсолютні значення знайдених на першому етапі помилок (|е_і |) з незалежною змінною у. Необхідно взяти абсолютні значення помилок, а не їх справжні значення, оскільки Σе=0 , і тому неможливо буде підібрати регресію е = f(у).

в) Оскільки фактична форма цієї регресії не відома, тому до неї необхідно підібрати різні форми кривих (користуючись набором ліній тернду у майстері офісних програм). Обирають ту регресію, яка найкраще підходить з огляду на коефіцієнт кореляції (або детермінації) та середні квадратичні відхилення параметрів b₀ та b₁. Існують випадки:

- b₀=0 та b₁<> 0, така ситуація називається "чиста гетероскедастичність";

- b₀ та b₁><0, цей випадок називається "змішана гетероскедастичність".

г) Застосувати t-тест для перевірки статистичної значимості параметрів b₀ та b1, якщо вони значно відрізняють­ся від нуля, то у моделі існує гетероскедастичність.

Перевага тесту Глейзера в тому, що він дає також інформацію про форму гетероскедастичності, тобто про спосіб, яким пов'язані е_і та у. Ця інформація є важливою, як ми зараз побачимо, для "корекції" гетероскедастичності.

Вилучення гетероскедастичності. Коли на базі будь-якого тесту встановлено гетероскедастичність, то для її вилучення змінюють початкову модель таким чином, щоб помилки мали постійну дисперсію. Далі невідомі параметри трансформованої моделі роз­раховуються за методом найменших квадратів. Трансформація моделі зводиться до зміни первісної форми моделі. Яким чином це проводиться, залежить від специфічної форми гетероскедастичності, тобто від форми залежності між дисперсією та значеннями незалежних змінних: =f(x_i). Розглянемо можливі випадки трансформації моделі на прикладі про­стої лінійної регресії. Припустимо, що ми маємо початкову модель y_i = β₀ + β₁x_i + е_i (де випадкова величина е_i гетероскедастична, але відпо­відає всім іншим класичним припущенням лінійної регресії.

1. Метод зважених найменших квадратів (ЗНК), який є особливим випадком методу узагальнених най­менших квадратів (УНК). У методі простих найменших квадратів мінімізують просту суму квадратів відхилень:

У якій кожне відхилення має однакову вагу (сума ваг =1). Тобто сума Σ є незваженою сумою квад­ратних відхилень, у якій припускається, що е_і, оцінені за допомогою е_і. Хоча, якщо дисперсія е_і не є сталою, зрозуміло, що більша дисперсія спостереження дає менш точну вказівку на те, де проходить правильна регресійна лінія. Досягнути сталості дисперсії е_і можливо надан­ням різної ваги кожній е_і (чи її оцінці). При цьому використовують вагу як частку 1/ , тобто ділять кожне відхилення на дисперсію випадкової величини. Отже, замість мінімізації про­стої суми квадратів відхилень мінімізують зважену суму квадратів відхилень:

Такий метод і називається методом зважених найменших квадратів (ЗНК). Прирівнявши часткові похідні зваженої суми квадратів до нуля і розв'язавши систему рівнянь, отримаємо формули для знаходження не­відомих параметрів b₀ та b₁, що можливо при відомій дисперсії .

2. Узагальнений метод найменших квадратів (метод Ейткена)

На відміну від звичайного методу найменших квадратів (МНК), узагальнений метод (УНК) враховує інформацію про неоднаковість дисперсії і тому здатний створити BLUE-оцінки, тобто оцінки, що мають найменшу дисперсію. Ідея УНК полягає в наступному. Маємо просту лінійну регресію:

Простою математичною маніпуляцією перепишемо попередній вираз у вигляді:

де x_0t = 1 для кожного і.

Припустимо, що наявна гетероскедастичність і всі дисперсії відомі. Поділимо всі елементи рівняння на σ_i, тоді отримаємо:

Для зручності перепишемо рівняння у вигляді:

де зірочками помічені початкові змінні, поділені на відомі σ_i. Позначення β₀* та β₁* використовуються для того, щоб відрізнити їх від звичайних пара­метрів β₀ та β₁, отриманих методом найменших квадратів. Тепер дисперсія трансформованої помилки е* є постійною величиною, тобто для останньої моделі зберігається припущення про гомоскедастичність, і ми переходимо до класичної регресійної моделі. Для того, щоб знайти невідомі параметри за методом узагальнених найменших квадратів, мінімізуємо:

або

За методом звичайних найменших квадратів невідомі параметри зна­ходяться шляхом мінімізації суми квадратів відхилень фактичних зна­чень від теоретичних. Для простої лінійної регресії маємо:

В узагальненому методі найменших квадратів мінімізується вираз, який можна переписати у вигляді:

де γ_i=1/σ_i* — вагові коефіцієнти.

Тобто в узагальненому методі найменших квадратів мінімізуємо зва­жену суму квадратів відхилень з вагами, обернено пропорційними до σ_i.