1. На внешней границе г1:

-постоянное давление

P(Г,t) = P = const (3)

т.е. граница является контуром питания;

-постоянный переток через границу

, (4)

где n – нормаль к границе Г;

- переменный переток через границу

(t); (5)

- замкнутая внешняя граница

0; (6)

- бесконечный по простиранию пласт

; (7)

2. На внутренней границе Г₂:

-постоянное давление на забое скважины радиуса

P(r =P ; (8)

- постоянный дебит. Это условие при выполнении закона Дарси можно представить следующим образом:

Q = (9)

или

r при r=r ; (10)

где F= - площадь боковой поверхности скважины, h – толщина пласта;

-переменное давление на забое скважины

P(r при r=r (11)

- переменный дебит

при r=r ; (12)

- отключение скважины

0 при r=r ; (13)

Основная литература: Осн.1 [39-45]

Дополнительная литература: Доп. 3 [44-51]

Контрольные вопросы:

1. Что понимается под контуром питания?

2. Начальные условия.

3. Условия на внешней границе

4. Условия на внутренней границе

Лекции №5. Установившаяся фильтрация несжимаемой жидкости –моделирование водонапорного режима разработки

Дифференциальное уравнение установившейся фильтрации несжимаемой жидкости

Если жидкость несжимаема, то ее уравнение состояния . Также пористость m=const. Тогда уравнение неразрывности потока примет вид:

(1)

Подставляя в (1) v , v , v , получим

0

или

(2)

Расчет основных гидродинамических характеристик одномерного прямолинейно-параллельного фильтрационного потока.

1. Пусть в горизонтальном пласте постоянной толщины h и ширины В на контуре питания поддерживается постоянное давление P , а на добывающей галерее, отстоящей на расстоянии Lк от контура питания (КП), постоянное давление P . Направляем ось координат ОХ вдоль линии тока, ось OY вдоль КП (рис. 1).

КП- Р_к скважины

Z B

галерея - Р_г

у h

O x

L_k

Рис. 1. Схема одномерного прямолинейно - параллельного фильтрационного потока

Так как меняется только координата x, то уравнение (2) принимает вид:

0 (3)

которое, решается при следующих граничных условиях

P=P при x=0;

P=P при x=L (4)

Дважды интегрируя (3) и удовлетворяя условиям (4) получим закон распределения давления в пласте:

P=P_k - (5)

найдем градиент давления

Тогда скорость фильтрации

= (6)

Дебит галереи определяется выражением

где, F=Bh – площадь поперечного сечения пласта.

с учетом (6) получим, что

(7)

Закон движения частицы жидкости найдем по формуле:

(8)

Разделяя переменные и учитывая (6), получим после интегрирования

(9)

Время полного выбора жидкости из пласта (Т) определяется по (9) при x=L

(10)

Средневзвешенное по объему пластовое давление (Р) найдем по формуле:

(11)

2. Расчет основных гидродинамических характеристик одномерного плоскорадиального фильтрационного потока.

Будем считать, что несжимаемая жидкость притекает к гидродинамически совершенной скважине радиусом r , расположенной в центре однородного горизонтального кругового пласта постоянной толщины h. На внешней круговой границе пласта радиусом r , служащей контуром питания, поддерживается постоянное давление Р , на забое скважине давление Р , тоже постоянно (рис. 2).

Дифференциальное уравнение в этом случае имеет вид:

0 (12)

Введя замену r= после соответствующих преобразований из (12) получим:

= 0 или = 0 (13)

Уравнение (13) будем решать при следующих граничных условиях:

P=P при r = r_к ;

P=P при r = r (14)

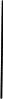
стенка скважины - Р_с

r_c контур питания - Р_к

r_k r_к

Рис. 2. Схема одномерного плоскорадиального фильтрационного потока

Дважды интегрируя (13) и учитывая (14), найдем закон распределения давления

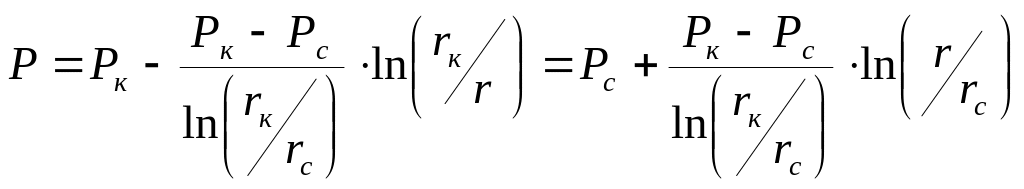(15)

Скорость фильтрации = (16)

Дебит скважины , где - поверхность, через которую происходит фильтрация с учетом (18) будем иметь

(17)

Формула (17) называется формулой Дюпюи.

Закон движения частицы жидкости найдем из формулы

или (18)

Подставив (18) в (21) и производя интегрирование в пределах от 0 до t и от r до r, получим (19)

Время Т полного отбора жидкости из пласта определяется из (19) подстановкой r = r , т. е. 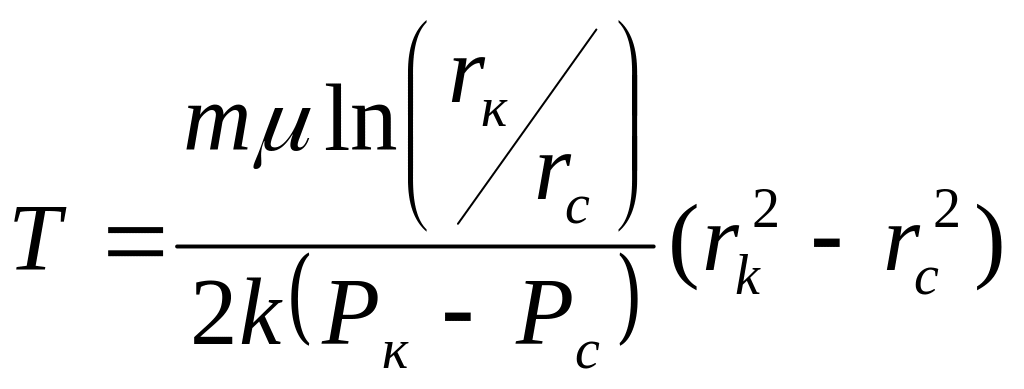(20)

Средневзвешенное по объему порового пространства пластовое давление определяется из формулы

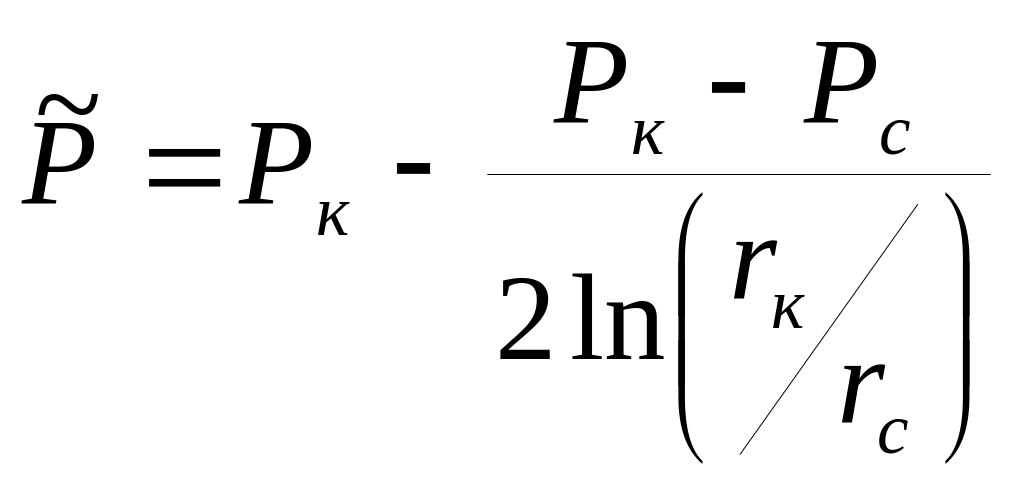(21)

Основная литература: Осн. 1 [51-68]

Дополнительная литература: Доп. 3 [51-65], 5[23-32]

Контрольные вопросы:

1. Установившаяся фильтрация.

2. Простейшие фильтрационные потоки.

3. Средневзвешенное по объему пластовое давление.

4. Формула Дюпюи.

5. Закон движения частицы.

Лекция № 6. Фильтрация жидкости в неоднородных пластах -моделирование реальных продуктивных пластов

В природных условиях продуктивные нефтегазосодержащие пласты редко бывают однородные.

Пористая среда называется неоднородной, если ее фильтрационные характеристики – пористость и проницаемость – различны в разных областях.

Нередко встречаются пласты, значительные области которых сильно отличаются друг от друга по фильтрационным характеристикам, так называемые макронеоднородные пласты.

В пластах-коллекторах нефти и газа выделяют следующие основные виды макронеоднородности.

1. Слоистая неоднородность, когда пласт разделяется по толщине на несколько слоев, в каждом из которых проницаемость в среднем постоянна, но отличается от проницаемости соседних слоев. Такие пласты называют также неоднородными по толщине. Вследствие малости кривизны границы раздела между слоями с различными проницаемостями считают обычно плоскими. Таким образом, в модели слоистой пористой среды предполагается, что проницаемость изменяется только по толщине пласта и является кусочно-постоянной функцией вертикальной координаты.

В случае прямолинейно-параллельного потока несжимаемой жидкости в слоисто-неоднородном пласте дебит потока Q всего пласта можно вычислить как сумму дебитов в отдельных пропластках Q (рис. 1).

(1)

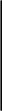
P_k P_г

k _n h _n Q _n

.

k_i . h_i Q_i

k₂ h₂ Q₂

k₁ h₁ Q₁

х

Рис. 1. Схема слоисто-неоднородного пласта в случае прямолинейно-параллельного потока

Для гидродинамических расчетов иногда бывает удобным заменить поток жидкости в неоднородном пласте потоком в однородном пласте такой толщины h, ширины В и длины L со средней проницаемостью , которая определяется выражением:

(2)

В случае плоскорадиального потока несжимаемой жидкости в слоисто-неоднородном пласте

(3)

и определяется по (2).

2. Зональная неоднородность, при которой пласт по площади состоит из нескольких зон (областей пласта) различной проницаемости. В пределах одной и той же зоны проницаемость в среднем одинакова, но на границе двух зон скачкообразно меняется. Здесь, таким образом, имеет место неоднородность по площади пласта.

В случае прямолинейно-параллельного потока несжимаемой жидкости в зонально-неоднородном пласте дебит потока всего пласта равен (рис. 2):

и (4)

где l – длина i – ой зоны, проницаемость которой k .

Р_к Р_г

Q _n

l₁ l₂ l₃ .. l_i . . l _n

k₁ k₂ k₃ .. k_i . . k _n

х

Рис. 2. Схема зонально- неоднородного пласта в случае прямолинейно-параллельного потока

Для плоскорадиального потока несжимаемой жидкости в зонально-неоднородном пласте дебит потока всего пласта равен:

и (5)

где r и r – внешний и внутренний радиусы i – ой зоны.

Основная литература: Осн. 1 [69-78]

Дополнительная литература: Доп. 3 [94-99], 5[73-80].

Контрольные вопросы:

1. Слоистая неоднородность пласта.

2. Зональная неоднородность пласта.

3. Средняя проницаемость пласта при слоистой неоднородности.

4. Средняя проницаемость пласта при зональной неоднородности.

Лекция 7. Приток жидкости к гидродинамически несовершенным скважинам – моделирование видов забоя скважин

Скважина называется гидродинамически совершенной, если она вскрывает продуктивный пласт на всю толщину h и забой скважины открытый, т. е. вся вскрытая поверхность забоя является фильтрующей (рис. 1а).

1. Если скважина с открытым забоем вскрывает пласт не на всю толщину h, а только на некоторую глубину b, то ее называют гидродинамически несовершенной по степени вскрытия пласта. При этом называется относительным вскрытием пласта (рис. 1б).

Дебит гидродинамически несовершенной по степени вскрытия пласта скважины можно определить по формуле И. Козени:

(1)

а ) б) в)

забой

b h отверстия или фильтр

Рис 1. Виды забоев скважин

2. Если скважина вскрыла пласт до подошвы (рис. 1в), но сообщение с пластом происходит только через специальные отверстия в обсадной колонне и цементном камне или через специальные фильтры, то такую скважину называют гидродинамически несовершенной по характеру вскрытия пласта.

3. Нередко встречаются скважины и с двойным видом несовершенства – как по степени, так и по характеру вскрытия пласта.

Дебит скважины гидродинамически несовершенной как по степени, так и по характеру вскрытия пласта можно рассчитать по формуле:

(2)

где – дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по степени вскрытия пласта и по характеру вскрытия .

Величины и определяются по методике В. И. Щурова. Им построены графики зависимости величины от параметров и и величины от трех параметров: , и , где n – число перфорационных отверстий на один метр вскрытой толщины пласта, – диаметр скважины, – глубина проникновения пуль в породу, - диаметр отверстий.

Иногда бывает удобно ввести понятие о приведенном радиусе скважин , т. е. радиусе такой совершенной скважины, дебит которой равен дебиту данной несовершенной скважины:

Тогда формулу (2) можно заменить следующей формулой:

(3)

Иногда гидродинамическое несовершенство скважин учитывается при помощи коэффициента совершенства скважины

(4)

где Q – дебит несовершенной скважины; – дебит совершенной скважины в тех же условиях.

Коэффициент совершенства скважины и величина С связаны между собой зависимостью:

(5)

Основная литература: 1 [69-78].

Дополнительная литература: 3 [94-99], 5[58-67].

Контрольные вопросы:

1. Совершенная скважина.

2. Несовершенство скважины по степени вскрытия.

3. Несовершенство скважины по характеру вскрытия.

4. Приведенный радиус скважины.

5. Влияние радиуса скважины на ее дебит.

Лекции № 8. Интерференция скважин - моделирование фильтрации жидкости при взаимодействии нескольких скважин в пласте

Явление интерференции (взаимодействия) скважин заключается в том, что под влиянием пуска, остановки или изменения режима работы одной группы скважин изменяются дебиты и забойные давления другой группы скважин, эксплуатирующих тот же пласт. Вновь вводимые скважины взаимодействуют с существующими. Это явление взаимодействия и взаимовлияния скважин называется интерференцией.

Назовем точечным стоком (источником) на плоскости точку, поглощающую (выделяющую) жидкость. Сток (источник) можно рассматривать как центр добывающей (нагнетательной) скважины.

Введем потенциал Ф точечного стока, определяемый по формуле:

(1)

где q=Q/h – дебит скважины-стока, приходящейся на единицу толщины пласта;

r – расстояние от стока до точки пласта, в которой определяется потенциал;

c – постоянное число.

Для точечного источника в формуле (1) дебит q считается отрицательным.

При совместном действии в пласте нескольких стоков (источников) потенциал Ф определяется для каждого стока (источника) по формуле (1). Потенциал, обуславливаемый всеми стоками и источниками, вычисляется путем сложения этих независимых друг от друга значений потенциалов, т. е. или

(2)

где .

1. Приток жидкости в группе скважин в пласте с удаленным контуром питания (КП) (рис. 1).

Пусть в горизонтальном пласте толщиной h расположена группа скважин А , А , … А радиусами r , работающих с различными забойными потенциалами , где i = 1,2,…n.

Расстояние между центрами i – ой j – ой скважин известны ( = ). Так как контур питания (КП) находится далеко от скважин, то можно приближенно считать, что расстояние от всех скважин до всех точек КП одно и то же и равно r . Потенциал Ф на КП считается заданным.

Ф_к

r₁₃ А₁, Ф₁

А₃ A_i ,Ф_i КП

r_3n Аn r_k

Ф_к

Рис. 1. Схема притока жидкости в группе скважин в пласте с удаленным контуром питания (КП)

Потенциал в любой точке пласта М определяется по формуле (2). Потенциал на забое i – й скважины

(3)

где i = 1,2, … n.

Система (3) состоит n уравнений и содержит (n+1) неизвестных (n дебитов и постоянную интегрирования С). Дополнительное уравнение получим, поместив точку М на контур питания.

(4)

Вычитая численно каждое из уравнений (3) из (4), исключим, постоянную C и получим систему из n уравнений, решив которую, можно определить дебиты скважин q если заданы забойные и контурный потенциалы.

2. Приток жидкости к скважине в пласте с прямолинейным контуром питания (КП)

Пусть в полубесконечном пласте с прямолинейным КП, на котором потенциал равен , работает одна добывающая скважина с забойным потенциалом . Необходимо найти q.

Для решения задачи зеркально отображаем скважину-сток относительно КП и дебиту скважины – отображению (источник) припишем знак минус.

Потенциал в любой точке пласта М:

(5)

Помещая последовательно точку М на стенку скважины (сток) радиуса r и на КП, найдем

(6)

где a – кратчайшее расстояние от скважины стока до КП.

3. Приток жидкости к скважине, эксцентрично расположенной в круговом пласте.

Пусть в плоском пласте постоянной толщины h с круговым КП радиуса r , на котором поддерживается постоянный потенциал , на расстоянии a от центра круга расположена скважина – сток с постоянным потенциалом .

Отобразим скважину-сток фиктивной скважиной-источником относительно КП.

Потенциал в точке М пласта определяем по формуле (5). Помещая точку М на стенку скважины и КП, определяем потенциалы и , после чего находим

(7)

Основная литература: Осн.1 [52-96]

Дополнительная литература: Доп. 3 [125-155], 5 [25-32].

Контрольные вопросы:

1. Явление интерференции скважин.

2. Источники и стоки

3. Дебит скважины в пласте с прямолинейным контуром питания.

4. Дебит скважины эксцентрично размешенной на залежи.