3. Методические указания к выполнению курсовой работы

3.1. План построения и содержание разделов пояснительной

записки

3.1.1. План построения пояснительной записки

Пояснительная записка состоит из следующих разделов:

- введение;

- часть 1, включающая подразделы:

- анализ геомеханических систем, включающих конструкции на грунтовом или породном основании;

- обзор и анализ существующих методов расчета конструкций, взаимодействующих с упругим основанием;

- расчет конструкций, взаимодействующих с грунтовым упругим основанием, по методу А.Н. Крылова;

- результаты расчета на персональных ЭВМ;

- 2 часть, включающая подразделы:

- определение нагрузки на подпорную стенку;

- определение устойчивости подпорной стенки на сдвиг;

- определение устойчивости подпорной стенки на опрокидывание;

- результаты расчета подпорных стенок на ПЭВМ;

- заключение.

3.1.2. Содержание введения

Во введении дается краткая оценка состояния геомеханических систем, включающих встречающиеся в практике ведения горных работ конструкции на упругом основании; обосновывается необходимость проведения расчетов таких систем на стадии проектирования; отмечается актуальность решаемых задач.

Во введении дается краткий анализ существующих типов подпорных стенок, обосновывается необходимость их применения на различных этапах освоения месторождений, производится оценка существующих методов расчета подпорных стенок

3.2. Расчет балок на упругом основании

3.2.1. Анализ геомеханических систем, включающих конструкции на грунтовом или породном основании

Данный раздел курсовой работы выполняется студентом на основе самостоятельной исследовательской работы с учебной, научно-технической литературой и нормативной и проектной документацией, по материалам которых проводится анализ встречающихся в практике ведения горных работ геомеханических систем, включающих различные типы конструкций, находящиеся под действием нагрузки и взаимодействующие с упругим грунтовым или породным основанием.

Описывается назначение таких конструкций, их напряженно-деформированное состояние на различных этапах установки, периодах ведения горных работ и стадиях проявления горного давления.

Отдельно характеризуются объекты, которые с высокой степенью схожести имитируются при расчетах балками, лежащими под нагрузкой на упругом основании.

Анализ сопровождается необходимыми графическими иллюстрациями и ссылками на используемые литературные источники.

3.2.2. Обзор и анализ существующих методов расчета

конструкций, взаимодействующих с упругим основанием

В разделе по данным анализа научно-технической литературы выделяются основные методы расчета балок на упругом основании, отражаются принципиальные различия между ними, отмечаются достоинства и недостатки. Также в данном разделе более подробно описывается один из существующих методов расчета (кроме метода академика А.Н. Крылова), характеризуются его расчетная схема, алгоритм и математическая модель, приводится пример расчета, фиксируются достоинства и недостатки.

Обзор и анализ также, как и в предыдущем разделе, сопровождается соответствующими рисунками и ссылками на используемые источники. По ходу анализа приводятся необходимые уравнения, которые нумеруются в соответствии с требованиями данных Методических указаний.

3.2.3. Расчет конструкций, взаимодействующих с грунтовым

упругим основанием, по методу А.Н. Крылова

В соответствии с алгоритмом расчета, предложенным академиком А.Н. Крыловым, данный раздел курсовой работы включает следующие этапы решения поставленной задачи:

на основании исходных данных строится расчетная схема, и определяются значения силовых и кинематических факторов в начальном и конечном сечениях балки;

производится разбиение балки на участки, и вычисляются значения базовых функций и их производных;

исходя из заданных граничных условий и на основании общих уравнений силовых и кинематических факторов, полученных А.Н. Крыловым, формируется система линейных уравнений, описывающих напряженно-деформированное состояние балки на упругом основании, и производится расчет неизвестных начальных параметров;

определяются значения поперечных сил, изгибающих моментов и вертикальных перемещений в сечениях балки, а также величина нагрузки на упругое основание по всей длине балки, для которых строятся эпюры.

Все уравнения, необходимые вычисления, таблица значений базовых функций и их производных и итоговые результаты расчета в виде эпюр фиксируются в записке.

Математическая модель расчета балки на упругом основании по методу акад. А.Н. Крылова заключается в следующем.

Рассмотрим балку, имитируемую стержнем, постоянного сечения, лежащую на упругом основании, которое в виде опорной среды препятствует прогибам балки (рис. 3.1).

Рисунок 3.1 - Расчетная схема балки на упругом основании

На рисунке приняты следующие обозначения: P₁ и P₂ - действующие на балку сосредоточенные нагрузки; (z) - угол поворота сечения балки с координатой z; X(z) - прогиб балки в том же сечении; P(z) - интенсивность реактивной нагрузки или сосредоточенная реактивная сила в том же сечении; L - длина балки.

Распределенная реактивная нагрузка (или сосредоточенная реактивная сила) P(z), обусловленная сопротивлением среды, зависит от прогибов X(z) в том же сечении, что соответствует модели «местных деформаций». В этой модели, соответствующей гипотезе Фусса-Винклера, не учитывается перераспределительная способность упругого основания, что для слабых малосвязных пород вполне допустимо.

Считается, что реактивные нагрузки прямо пропорциональны перемещениям балки:

, (3.1)

где  - коэффициент жесткости упругого основания, часто называемый» коэффициентом упругого отпора пород», измеряемый в кН/м.

При условной ширине балки, равной 1 м, для грунтов средней плотности  изменяется в пределах от 50 до 500 кН/м, а для более плотных - от 500 до 1000 кН/м²; для каменной кладки  = (0,4–0,6)10⁵ kH/м²; для бетона -  = (0,8-1,5)10⁵ кН/м². Два последних диапазона изменения коэффициента отпора являются наиболее подходящими и для подземных горных пород.

Дифференциальное уравнение прогибов балки, называемое дифференциальным уравнением упругой линии балки, лежащей на простом упругом (Винклеровском) основании, имеет вид:

, (3.2)

где EI(z) - изгибная жесткость балки; E - модуль упругости материала балки; I - момент инерции поперечного сечения балки) как функция координаты z; q(z) - распределенная "активная" нагрузка, действующая на балку.

Для балки постоянного сечения, когда , уравнение (3.2) преобразовывается в следующий вид:

(3.3)

Для расчетной схемы, представленной на рис. 3.2, академик А.Н. Крылов получил решение этого уравнения через нормальные фундаментальные функции (функции А.Н. Крылова) в общем виде:

(3.4)

где и - единичные разрывные функции; , , , - функции А.Н. Крылова (функции влияния);

(4.5)

X₀,_,M₀ и Q₀ - соответственно перемещение, угол поворота, изгибающий момент и поперечная сила в начальном (нулевом) сечении балки; q(s) - интенсивность заданной ("активной") нагрузки в сечении с координатой s; a_i и b_i - расстояния от начала координат до точек приложения изгибающего момента M_i и сосредоточенной силы P_i (см. рис. 3.2).

Рисунок 3.2 - Расчетная схема балки по методу акад. А.Н. Крылова

При равномерно распределенной нагрузке (q(s)= const) интеграл в последнем слагаемом выражения (3.4) берется легко, однако в практических расчетах распределенную нагрузку можно заменить эквивалентной системой сосредоточенных сил. Аналогично можно поступать и при любых других законах распределения нагрузок. Точность расчета будет зависеть только от шага разбиения распределенной нагрузки.

При отсутствии упругого основания, которое характеризуется величиной B=0, (при таком условии =0), получим:

В результате для этого частного случая уравнение (4.4) трансформируется в выражение:

(3.6)

В данном виде уравнение (3.6) в совокупности с другими уравнениями, которые могут быть получены при его дифференцировании (для углов поворотов сечений, изгибающих моментов и поперечных сил), чаще всего используется при расчете статически неопределимых систем методом начальных параметров.

Дифференцируя уравнение (3.4), получим уравнение угла поворота вертикальных сечений балки:

(3.7)

Дифференцируя уравнение (3.7) и умножая на EI, получаем выражение для изгибающего момента в произвольном сечении балки:

(3.8)

Дифференцируя выражение (3.8), получаем уравнение поперечной силы:

(3.9)

В уравнениях (3.7),(3.8) и (3.9): _q(z), M_q(z) и Q_q(z) - слагаемые от влияния распределенной нагрузки, вид которых определяется функцией q(s), входящей в подынтегральное выражение уравнения (3.4).

Так, при равномерно распределенной нагрузке q(s)=q=const, действующей по всей длине балки, раскрывая интеграл в уравнении (3.4), получаем:

(3.10)

В тех случаях, когда равномерная нагрузка распределена на расстоянии C от начала отсчета координаты z, выражения (3.10) также остаются в силе, только в них вместо z необходимо подставить (z-c).

С помощью полученных уравнений (3.4),(3.6)-(3.10), зная начальные параметры X₀, _, М₀, Q₀ легко найти значения прогибов, углов поворота сечений, изгибающих моментов и поперечных сил в любом сечении балки на упругом основании, изменяя z от 0 до L.

Неизвестные начальные параметры (для данной задачи их всегда два) находятся из условий на правом конце балки. Так, например, для балки со свободными концами имеем:

в начальном сечении Q₀ = 0 и M₀ = 0;

в конечном сечении Q(L)= 0 и M(L)= 0.

Составив теперь уравнения вида (3.8) и (3.9) с учетом указанных условий, получаем систему двух уравнений с двумя неизвестными X₀ и _, значения которых и находятся из решения этой системы.

Если же на свободных концах балки приложены сосредоточенные силы P₀, P_L и сосредоточенные моменты M₀, M_L, то граничные условия будут выглядеть следующим образом: Q₀=P₀; Q(L)=P_L; M₀=M₀; M(L)=M_L. При шарнирном опирании конца балки: M=0 и X=0. При жестком защемлении – X=0 и  =0.

Таким образом, представленная математическая модель является универсальной, так как позволяет производить расчеты балок на упругом основании при любых видах нагрузки и граничных условий.

3.2.4. Пример расчета балки на упругом основании по методу

акад. А.Н.Крылова

Расчетная схема незакрепленной на концах балки на упругом основании для данного примера представлена на рис. 3.3.

Исходные данные: b₁=1 м; b₂=3 м; L=6 м; EI=5,610⁵ кНм; =1,410⁵ кН/м²; P₁=1000 кН; P₂=2000 кН.

Рисунок 3.3 - Расчетная схема

На основании действующей системы сил, точек их приложения и при условии отсутствия всякого закрепления балки на концах граничные параметры формируются следующим образом:

если z = 0, то Q₀ = 0 и M₀ = 0;

если z = L, то Q(L) = 0 и M(L) = 0.

Определяем по формуле (4.5) значение .

Разбиваем балку сечениями на участки. Принимаем 12 участков. Для полученных сечений, каждое из которых имеет свою координату Z = iL/12 (i = 0,1,2,...,12 - порядковые номера сечений), вычисляем значения базовых функций, которые представим в табличной форме (табл. 3.1).

Используя общие уравнения (3.9) и (3.8), запишем уравнения поперечных сил и изгибающих моментов для правого (z = L) конца балки на упругом основании:

Полученные равенства представим в виде системы линейных уравнений:

(3.11)

где ; ; ; ; ; .

Таблица 3.1 - Числовые значения базовых функций акад. А.Н. Крылова

Базовая функция	Значения базовых функций при βz, равном:
	0,00	0,25	0,50	0,75	1,00	1,25	1,50	1,75	2,00	2,25	2,50	2,75	3,00
	1,00	0,99	0,99	0,95	0,83	0,59	0,17	-0,53	-1,57	-3,01	-4,91	-7,25	-9,97
	0,00	0,25	0,49	0,75	0,97	1,15	1,25	1,21	0,95	0,39	-0,59	-2,10	-4,25
	0,00	0,03	0,13	0,28	0,49	0,76	1,06	1,37	1,65	1,83	1,81	1,49	0,71
	0,00	0,00	0,02	0,07	0,17	0,32	0,56	0,85	1,23	1,57	2,13	2,55	2,83

Из полученной системы уравнений в общем виде находим:

; .

После подстановки численных величин определяем значения коэффициентов в системе уравнений:

;

;

;

;

.

Подставив значение коэффициентов, в результате получим:

рад и м.

Таким образом, теперь известны значения всех четырех начальных параметров (X₀, _, M₀, Q₀), на основании которых по уравнениям (3.4), (3.7), (3.8) и (3.9) легко находятся вертикальные перемещения X(z), углы поворота Q(z),изгибающие моменты M(z)и поперечную силу Q(z) во всех интересующих сечениях балки. По рассчитанным значениям перемещений, моментов и поперечных сил строятся эпюры, общий вид которых приведен на рис. 3.4-3.6. Отдельно строится рассчитанная по формуле (3.1) эпюра давления балки на упругое основание (эпюра распределенного распора основания), показанная на рис. 3.7. На рис. 3.4-3.6 в скобках проставлены результаты аналогичного расчета на ПЭВМ, которые имеют высокую степень сходимости с теоретическими расчетами с привлечением базовых гиперболических функций акад. А.Н. Крылова.

Рисунок 3.4 – Эпюра поперечных сил в сечениях балки

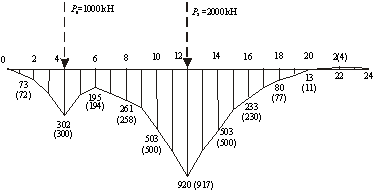
Рисунок 3.5 – Эпюра изгибающих моментов в сечениях балки

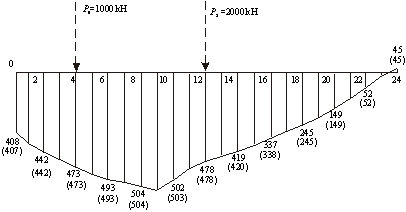
Рисунок 3.6 – Эпюра вертикальных перемещений X(z)10⁵ балки

Рисунок 3.7 – Распределение давления балки на упругое основание

3.3. Расчет устойчивости подпорных стенок

3.3.1. Определение нагрузок на подпорную стенку

Данный раздел курсовой работы включает следующие этапы:

- с помощью геометрических построений методом Понселе на рисунке выделяется треугольник Ребхана; при этом дается описание выполняемых на рисунке процедур;

- на основании ряда тригонометрических теорем определяется площадь треугольника Ребхана; порядок расчета фиксируется в записке;

- рассчитывается угол  плоскости обрушения грунта;

- определяется давление грунта на подпорную стенку и координаты точек приложения сосредоточенных сил;

- определяются нагрузки (в виде сосредоточенных сил) и координаты их приложения от собственного веса стенки;

- производится расчет и построение эпюры нагрузки на подпорную стенку (эпюры напряжений).

Все этапы данного раздела сопровождаются необходимыми графическими построениями и расчетами, которые фиксируются в записке.

3.3.2. Определение устойчивости подпорной стенки на сдвиг

Конечной целью выполнения расчетов в данном разделе является определение коэффициента устойчивости на сдвиг. Для этого суммируются все удерживающие силы (пассивные) и все сдвигающие силы (активные). Отношение суммы первых к сумме вторых дает искомый коэффициент. Все силы должны быть разделены на вертикальные и горизонтальные составляющие. Первые при этом увеличивают силу трения подпорной стенки по основанию.

3.3.3. Определение устойчивости подпорной стенки

на опрокидывание

Итоговым для данного раздела является определение коэффициента устойчивости на опрокидывание относительно наружного ребра подпорной стенки. Для этого вычисляются моменты всех удерживающих и опрокидывающих сил, а отношение сумм этих моментов друг к другу дает коэффициент устойчивости. Удерживающими силами являются, как правило, веса отдельных участков стены, а опрокидывающими - активные силы давления грунта.

Расчет моментов производится на основании произведения сил на соответствующие плечи относительно наружного ребра. Плечи вычисляются с помощью тригонометрических преобразований как перпендикуляры, восстановленные из точки наружного ребра к линии действия сил.

3.3.4. Результаты расчета подпорных стенок на ПЭВМ

Данный раздел включает полученную на ПЭВМ распечатку, состоящую из двух частей. Первая часть отражает результаты выполнения общего задания на курсовую работу, вторая - содержит параметры исследования на ПЭВМ влияния варьирования исходных данных на конечные результаты расчета. По результатам исследования строятся соответствующие графики.

3.3.5. Содержание заключения

В заключении отражаются следующие выводы по результатам курсовой работы:

сравнение полученных ручным и машинным путем результатов расчета;

сравнение заданных и рассчитанных коэффициентов устойчивости с общим выводом по устойчивости подпорной стенки;

вывод по экспериментальным исследованиям на ПЭВМ взаимовлияния параметров.

3.3.6. Методические указания к выполнению отдельных разделов

расчета устойчивости подпорных стенок

Построение Понселе.

Классическим методом определения давления на подпорную стенку является использование второй теоремы Ребхана, по которой давление грунта на ограждающую поверхность равно площади треугольника IHG (треугольника Ребхана, рис. 3.8), умноженной на объемный вес.

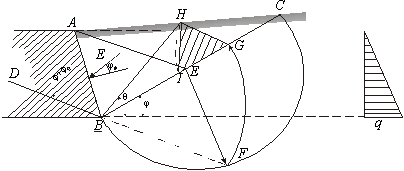
Рисунок 3.8 – Построение Понселе

Для решения этой задачи применяется построение Понселе, выполняемое следующим образом:

- проводится линия BC под углом естественного откоса  к горизонту до пересечения с поверхностью грунта;

- на отрезке BC как на диаметре строится полуокружность;

проводится основная линия BD под углом ( + _) к ограждающей поверхности;

- из верхней точки A проводится прямая AE, параллельная основной BD, до пересечения с линией естественного откоса;

- из точки E восстанавливается перпендикуляр до пересечения с полуокружностью в точке F;

- радиусом BF делается засечка на линии BC в точке G;

- из точки G до пересечения с поверхностью грунта в точке H проводится прямая, параллельная основной линии BD;

- соединение H с B дает след плоскости обрушения грунта с углом наклона к горизонтали ;

- радиусом GH делается засечка на линии BC в точке I.

Полученный треугольник IHG является треугольником Ребхана. Площадь S_IHG, умноженная на объемный вес грунта γ, дает его давление E на подпорную стенку или распор (в кН/м):

Е = γS_IHG. (3.12)

Определение эпюры напряжений.

Так как интенсивность нагрузки меняется пропорционально высоте, эпюра нагрузки, которую на практике чаще всего называют эпюрой напряжений, имеет вид треугольника с наибольшей ординатой внизу. Обычно эпюру выносят в сторону, как это показано на рис. 3.8, а ординаты откладывают горизонтально от вертикальной оси. Нижняя ордината эпюры в этом случае определяется из условия, что площадь эпюры равна распору qh/2 = E, откуда:

. (3.13)

Ординаты эпюры отражают нагрузку на единицу площади вертикальной проекции подпорной стенки. Равнодействующая E нагрузки (или распор) проходит через центр тяжести эпюры, образуя с нормалью к подпорной стенке угол _.

Влияние пригрузки на поверхность грунта.

В данном случае не имеет значения, какая именно нагрузка приложена: слои сыпучего грунта, щебень, гравий, вообще какой-либо груз. Главным является интенсивность нагрузки. Для проведения расчетов нагрузка снимается и заменяется эквивалентным слоем грунта, который имеет вес, равный данной нагрузке. При этом толщина эквивалентного слоя может быть легко найдена по формуле (в м):

. (3.14)

Для поддержания эквивалентного слоя ограждающую поверхность поднимают до точки A' (рис. 3.9), а стена имеет высоту не h, а (h+h₀). Давление на стенку A'B находится при помощи построения Понселе; эпюра напряжений изобразится треугольником с высотой (h+h₀). Произведя обратную замену эквивалентного слоя заданной нагрузкой, верхняя часть эпюры высотой h₀ отбрасывается. В результате эпюра принимает вид трапеции. Необходимо помнить, что координаты точки приложения равнодействующей давления на стенку определяются теперь по центру тяжести трапеции.

Рисунок 3.9 – Схема к учету пригрузки на поверхность грунта

Частный случай.

Здесь частный случай отражается неравенством 90-_, которое характеризует такую ситуацию, когда линия AE, параллельная основной, пересекается с линией естественного откоса выше поверхности грунта. В данном случае также применимо построение Понселе, но полуокружность нужно строить не на BC (см. рис. 3.8), а на BE (рис. 3.10).

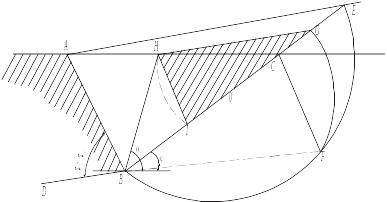
Рисунок 3.10 – Построение Понселе для частного случая

Ломаное очертание поверхности подпорной стенки.

На практике часто встречаются случаи, когда ограждающая поверхность имеет ломаное очертание. Тогда определение давления на подпорную стенку осуществляется в следующем порядке (рис. 3.11, а):

обычным порядком выполняется построение Понселе для верхней части стенки AB₁; определив для нее площадь треугольника Ребхана, находится распор E₁ и строится эпюра напряжений abf;

затем нижняя часть стенки B₁B₂ продолжается до поверхности грунта, в результате чего формируется фиктивная стенка A'B₂; для фиктивной поверхности A^’B₂ осуществляется построение Понселе, находится распор E₂ выполняется эпюра напряжений gcd;

отбрасывается верхняя часть gbe эпюры gcd, так как в верхней части ограждающая поверхность идет по линии AB₁, а не по A'B₁, и эпюра для этой части уже построена; в результате окончательная эпюра напряжений представляется фигурой acdef.

Как видно из рисунка, против точки перелома B₁ отмечается резкое изменение напряжений: плоскость AB₁ с большим наклоном имеет давление выше по сравнению с плоскостью B₁B₂ с меньшим углом наклона. Если бы ограждающая поверхность имела очертание согласно рис. 3.11, б, то уступ в эпюре был бы в другую сторону.

а - при выпуклом очертании передней поверхности стенки;

б - при вогнутом очертании передней поверхности стенки

Рисунок 3.11 – Построение Понселе и формирование эпюры напряжений

Слоистое строение грунта.

Иногда грунт, поддерживаемый подпорной стенкой, имеет слоистое строение: например, до некоторой глубины залегает глина, а ниже - песок. В этом случае находится сначала распор для верхнего слоя и строится эпюра напряжений. Затем верхний слой заменяется эквивалентным слоем грунта, находящегося в нижней части. Строится эпюра на всю высоту стенки, отбрасывается ее верхняя часть, поскольку для нее эпюра уже построена. Если углы естественного откоса для верхнего и нижнего слоев одинаковы и эти слои различаются только объемным весом, эпюра напряжений будет иметь перелом без уступа (рис. 3.12, а, б). Если углы естественного откоса разные, в эпюре напряжений появляются уступы видов, изображенных на рис. 3.12, в, г.

Рисунок 3.12 – Характер эпюр при слоистом строении грунта

Особого внимания при выполнении курсовой работы требует сочетание ломаных поверхностей подпорных стенок со слоистым строением поддерживаемых грунтов. При этом необходимо совместить методы, описанные для частного случая, ломаного очертания поверхности стенки и слоистого строения грунта.

Расчет коэффициента устойчивости подпорной стенки на сдвиг и опрокидывание.

Каждая подпорная стенка, поддерживающая грунт, в состоянии выполнять свое назначение, если она достаточно устойчива. Неудачно запроектированная конструкция может потерять устойчивость или вследствие опрокидывания около нижнего наружного ребра или вследствие сдвига (скольжения) по основанию.

Степень безопасности подпорной стенки в отношении потери ею устойчивости измеряется коэффициентом устойчивости: на опрокидывание k_опр, на сдвиг k_сдв. В общем случае они представляют отношение величины активных сил, при которых происходит разрушение, к величине активных сил, имеющихся в действительности. Таким образом, при определении коэффициентов устойчивости в числителе следует помещать только пассивные (удерживающие) силы, в знаменателе - только активные (сдвигающие или опрокидывающие) силы, но при этом - учитывать знаки. Чем больше коэффициенты, тем стена устойчивее, но всегда они должны превышать 1. На практике чаще всего за допускаемый коэффициент устойчивости принимают обычно 1,5. Поэтому должны соблюдаться условия:

и .

Для определения коэффициентов устойчивости необходимо установить все нагрузки, действующие на подпорную стенку. К таким нагрузкам относится, прежде всего, собственный вес стены. Вес каждой части стены G₁, G₂, G₃ (рис. 3.13) определяется умножением ее площади в плоскости рисунка на объемный вес кладки. Силы приложены в центрах тяжести соответствующих частей поперечного сечения стены.

Рисунок 3.13 – Обобщенная схема к расчету устойчивости стенок

На подпорную стену, кроме того, действует распор от поддерживаемого ею грунта. Равнодействующие давлений, как отмечалось выше, приложены в центрах тяжести соответствующих участков эпюры. Координаты центров тяжести переносятся по горизонталям к поверхности стены и указываются направления сил E₁, E₂, E₃ (см. рис. 3.13), составляющие угол _ с нормалями.

В общем случае также к противоположной стороне фундамента стены должен быть приложен отпор Q₃ (рис. 3.14), но при проверке устойчивости на опрокидывание он, как правило, не учитывается, так как влияние его весьма мало. В данной курсовой работе отпор Q₃ при расчете на опрокидывание также не учитывается.

Рисунок 3.14 – К эквивалентности сил на фундаменте стенки

При расчете на сдвиг по основанию влияние отпора Q₃ больше. Однако, так как эпюры распора слева (ABC) и справа (KACT) фундамента ограничены прямыми, проведенными под одним и тем же углом, то часто отбрасываются взаимно уравновешивающиеся части эпюр, т.е. треугольники ABC. В результате эпюра с правой стороны срезается по вертикали в пределах высоты фундамента и представляет собой прямоугольник KABT.

Установив все нагрузки, приложенные к подпорной стенке, переходят к расчету коэффициентов устойчивости. Коэффициент устойчивости на сдвиг указывает, во сколько раз должны увеличиться активные силы, чтобы произошел сдвиг. Он равен отношению суммы удерживающих сил к сумме сдвигающих сил:

. (3.15)

Удерживающими силами являются сила трения по подошве, вызванная весом подпорной стены, а также горизонтальная составляющая отпора Q₃ (см. рис. 3.14). Но, как уже говорилось выше, действие отпора нейтрализуется частью сил распора.

К сдвигающим силам относятся силы давления грунта. К каждому участку стены приложены наклонные силы E, имеющие горизонтальные составляющие и вертикальные . Последние увеличивают силу трения по подошве. Однако их нельзя считать удерживающими силами. Они активные, а вызываемую ими силу трения следует вычитать из сдвигающих сил.

Обозначая коэффициент трения через , для профиля стенки (см. рис. 3.13) без учета отпора Q₃ и эквивалентной ему части распора E₃ (также пренебрегая действиями их вертикальных составляющих) получим в общем виде следующее уравнение:

. (3.16)

Коэффициентом устойчивости на опрокидывание называют отношение суммарного момента удерживающих сил к суммарному моменту опрокидывающих сил:

. (3.17)

Для определения моментов необходимо, используя геометрические построения и преобразования, вычислить плечи всех сил, представляющие перпендикуляры (см. рис. 3.13), восстановленные из точки A к направлениям действия всех сил. Для профиля взятой за пример стенки имеем:

, (3.18)

где l_i и e_i - плечи (или эксцентриситеты) сил G_i и E_i.

Если направление какой-либо силы E проходит ниже ребра (точка A), то момент этой силы берется со знаком минус.

В заключение необходимо отметить, что если подпорная стенка проектируется с уступами со стороны грунта, то к удерживающим силам следует относить вес грунта на уступах (здесь влиянием дополнительной нагрузки пренебрегают). Влияние веса грунта на обрезе фундамента обычно столь незначительно, что им также можно пренебречь.

3.4. Оформление пояснительной записки

3.4.1. Требования к структуре пояснительной записки

Пояснительная записка должна содержать необходимые структурные части, размещаемые в следующей последовательности:

- титульный лист (прил. 3);

- задание на курсовую работу (см. прил. 2);

- аннотация;

- содержание;

- введение;

- основная часть;

- заключение;

- список использованных источников.

В аннотации следует указывать сведения об объеме курсовой работы: число страниц, рисунков, таблиц, количество использованных источников. После этого в аннотации приводятся краткие сведения о содержании и назначении работы и принятых решений.

Содержание должно включать нумерацию и наименование всех разделов, подразделов и пунктов с указанием номеров страниц, на которых размещается начало соответствующего текста. Введение, основная часть и заключение содержат весь необходимый материал в соответствии с положениями разд. 3 настоящих методических указаний.

Список использованных источников должен содержать перечень необходимой литературы, оформленный в соответствии с ГОСТом.

3.4.2. Требования к оформлению пояснительной записки

Пояснительная записка должна быть подготовлена автором в ручном или машинописном варианте на белой бумаге формата А4 (210х297). При подготовке текста и выполнении рисунков оставляются поля размерами: левое - не менее 30 мм, правое - 10 мм, верхнее - 15 мм, нижнее - 20 мм.

Текст основной части делится на разделы, подразделы и пункты. Заголовки разделов следует писать (печатать) заглавными буквами, располагая его симметрично тексту и отделяя от последнего пустой строкой. Каждый раздел должен начинаться с новой страницы. Перед заголовком ставится номер раздела. Подразделы (пункты) нумеруются с учетом номера раздела (подраздела) и отделяются от него точкой. Точки в конце заголовков не ставятся. Введение, заключение, список использованных источников не нумеруются.

Нумерация страниц сквозная, производится арабскими цифрами в середине верхней части листа. Титульный лист является первой страницей, но номер на нем не проставляется.

Все иллюстрации, помещенные в тексте, именуются рисунками, которые выполняются карандашом или тушью.

Рисунки, таблицы и формулы имеют сквозную нумерацию, в которой первое число отражает номер раздела, а второе - номер рисунка таблицы, формулы. Номер формулы заключается в круглые скобки и помещается с правой стороны на уровне нижней строки формулы. Уравнения с подставленными конкретными значениями не нумеруются. После каждой формулы обязательна расшифровка смысла используемых символов; в случае их повторения в последующем расшифровка не требуется.

По тексту записки обязательны ссылки на рисунки, таблицы, формулы, которые размещают сразу после первого упоминания о них. При этом слова пишутся сокращенно, а для формул указывается только их номер, заключенный в круглые скобки.

При ссылке по тексту на литературные источники приводится порядковый номер из общего списка, заключенный в косые скобки.

Обязательным является выражение единиц измерений по международной системе единиц (СИ).