2.3 Пример решения оптимизационных задач методом производных

Задача. Необходимо выбрать такое соотношение между длиной и шириной садового участка в виде прямоугольника, чтобы при заданной фиксированной длине изгороди площадь участка была максимальной.

Решение. Обозначим длину участка а, ширину участка b (рисунок 4).

Рисунок 4

Длина изгороди (периметр) участка заданы, т.е.

p = 2(a+b) = const. (1)

Площадь участка по условию задачи должна быть максимальное, т.е.

S = a*b = max. (2)

Это целевая функция данной задачи. Выразим из (1) ширину через длину и периметр

b = 0,5p – a. (3)

Подставим это выражение в (2) и получим

S = a*b = 0,5pa – a² = max. (4)

Исследуем (4) на экстремум по переменной а. Для этого возьмём производную и приравняем ее к нулю. В результате получим a = 0,25p. Подставим это значение в (3) и получим формулу для ширины

b = 0,5p – 0,25p = 0,25p.

Таким образом, окончательный результат

a = b = 0,25p.

Таким образом, участок прямоугольной формы с фиксированной длинной периметра будет иметь максимальную площадь при условии, если этот участок квадрат, т.е. ширина равна длине. Так как стоимость изгороди пропорциональна ее длине, то мы решили оптимизационную задачу: как при фиксированной стоимости на изгородь оградить её максимальную площадь в форме прямоугольника.

2.4 Пример решения оптимизационных задач графическим методом

Рассмотренную задачу в п.2.3 можно решить графическим способом, если выразить площадь S через один из параметров прямоугольника, Тогда получим параболу, у которой легко найти максимум (минимум, используя целые значения) (рисунок 5). Следует заметить, что минимум будет достигнут в двух точках.

1

2

2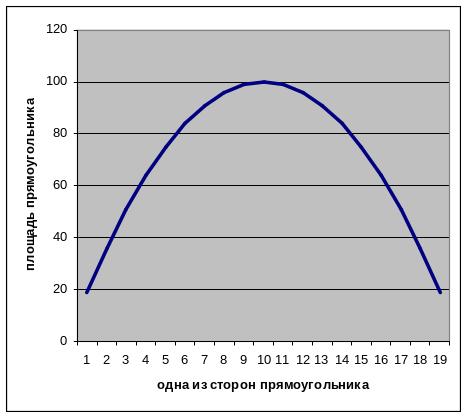

Рисунок 5 – Решение задачи графическим способом:

точка 1 – точка максимума

точка 2 – точки минимума

3. Выполнение контрольной работы

Контрольная работа выполняется по одному из вариантов, приведенных в следующем разделе.

Пояснительная записка должна отражать ход выполнения контрольной работы.

3.1 Оформление пояснительной записки

Для защиты работы студент должен представить пояснительную записку.

Содержание пояснительной записки к работе следует разделить на разделы и подразделы; разделы должны иметь порядковые номера, обозначенные арабскими цифрами. Подразделы должны иметь порядковые номера в пределах каждого раздела. Каждый раздел должен начинаться с нового листа, а каждый пункт записывается с абзаца. Наименование раздела записывается в виде заголовков прописными буквами, а подразделов – строчными (кроме первой прописной). Точку в конце заголовка не ставят.

В начале пояснительной записки помещают содержание, в конце – список литературы.

Пояснительная записка имеет следующую структуру:

Введение

1. Задание (по варианту)

2. Решение задачи классическим способом

3. Решение задачи графическим способом

Заключение

Литература

3.2 Содержание разделов

В разделе «Введение»:

необходимо определить и дать краткую характеристику понятию «Основы математического моделирования социально-экономических процессов».

В разделе «Задание»:

должно быть изложено задание (условие задачи) в соответствии с вариантом. Вариант выбирается по последней цифре зачетной книжки.

В разделе «Решение задачи классическим способом»:

должны быть представлено решение задачи методом производных, пример которого представлен в теоретической части п. 2.3.

Раздел «Решение задачи графическим способом»:

должны быть представлено решение задачи графическим методом, пример которого представлен в теоретической части п. 2.4.

В разделе «Заключение»:

необходимо дать краткую характеристику выполненной работы.

В разделе «Литература» приводится список используемой литературы.