Преп. Матвеева Т.К. для 114, 115 групп 10.02.2013

Задание 1. Язык паскаль. 1 вычисление корней уравнений и определенных интегралов

ПОСТАНОВКА ЗАДАЧИ

С заданной точностью eps вычислить площадь плоской фигуры, ограниченной тремя кривыми, уравнения которых y=f1(x), y=f2(x) и y=f3(x) определяются вариантом задания.

При решении задачи необходимо:

 с некоторой точностью eps1 вычислить абсциссы точек пересечения кривых, используя предусмотренный вариантом задания метод приближенного решения уравнения F(x)=0; отрезки, где программа будет искать точки пересечения и где применим используемый метод, определить вручную;

 представить площадь заданной фигуры как алгебраическую сумму определенных интегралов и вычислить эти интегралы с некоторой точностью eps2 по квадратурной формуле, предусмотренной вариантом задания.

Величины eps1 и eps2 подобрать вручную так, чтобы гарантировалось вычисление площади фигуры с точностью eps.

ВАРИАНТЫ ЗАДАНИЯ

Во всех вариантах eps = 0.001.

А. Уравнения кривых y =f_i(x):

1) f1= 2^x+1 f2= x⁵ f3= (1–x)/3

2) f1= 3(0.5/(x+1)+1) f2= 2.5x–9.5 f3= 5/x (x>0)

3) f1= exp(–x)+3 f2= 2x–2 f3= 1/x

4) f1= exp(x)+2 f2= –1/x f3= –2(x+1)/3

5) f1= 0.35x²–0.95x+2.7 f2= 3^x+1 f3= 1/(x+2)

6) f1= 0.6x+3 f2= (x–2)³–1 f3= 3/x (x>0) | (x<0)

7) f1= ln(x) f2= –2x+14 f3= 1/(2–x)+6

8) f1= exp(x)+2 f2= –2x+8 f3= –5/x

9) f1= 3/((x–1)²+1) f2= sqrt (x+0.5) f3= exp(–x)

10) f1= 1+4/(x²+1) f2= x³ f3= 2^–x

11) f1= |x| x⁵ f2= 2^x+1 f3= (1–x)/3

12) f1= 1/x f2= 1.5x–2 f3= exp(–x)+3

13) f1= 4^x+1 f2= 1/(x+2) f3= 0.35x²–0.95x+2.7

Б. Методы приближенного решения уравнений:

1) метод деления отрезка пополам;

2) метод хорд (секущих);

3) метод касательных (Ньютона);

4) комбинированный метод (хорд и касательных).

В. Квадратурные формулы:

1) формула прямоугольников;

2) формула трапеций;

3) формула Симпсона (парабол).

¹ Н.П.Трифонов, В.Н.Пильщиков Задания практикума http//cmcmsu.no-ip.info/1course/

Требования к программе и результатам.

1. В программе предусмотреть печать следующих результатов:

• абсцисс и ординат точек пересечения кривых с указанием выбранных отрезков и точности eps1,

• площади S заданной фигуры и площадей S_i, ее составляющих S (S=ΣS_i), с указанием точности eps2, начального разбиения и окончательного количества точек после удвоения.

2. Описать в программе процедуру root(f,g,a,b,eps,x), вычисляющую с точностью eps корень x уравнения f(x)=g(x) на отрезке [a,b]. (Если используется метод касательных или комбинированный метод, то у root должны быть еще параметры pf и pg - производные функций f и g.).

3. Описать в программе функцию integral(f,a,b,eps), вычисляющую с точностью eps величину определенного интеграла от функции f(x) на отрезке [a,b].

4. Процедуру root и функцию integral следует предварительно протестировать.

5. Оформить бланк отчета.

ЛИТЕРАТУРА

1. Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ. Т. 1 - М.: Наука, 1985 ( гл.11 с473, с482 ) .

или Ильин В.А., Поздняк Э.Г. Основы математического анализа. Часть 1 – М.,ФизМат, 1971 (гл.12 сс387-409).

2. Абрамов В.Г., Трифонов Н.П., Трифонова Г.Н. Введение в язык Паскаль. - М.: Наука, [1988 (гл.9 сс185-190 ).] 2011 (гл.5 сс114-129; гл.9 сс227-230-233 ).

3. Епанешников А.М., Епанешников В.А. Программирование в среде Turbo Pascal 7.0 - М.: "ДИАЛОГ-МИФИ", 2000 (сс48-49, сс54-65 ).

или Фаронов В.В. Программирование на персональном ЭВМ в среде Турбо паскаль. – М, МГТУ, 1990 (гл.9 сс161-163).

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

1. Для корректного применения предложенных методов приближенного решения уравнения F(x) = 0 (где F(x) = f(x)–g(x)) необходимо найти отрезок [a,b], на котором уравнение имеет ровно один корень. Достаточное условие для этого таково: на концах отрезка функция F(x) имеет разные знаки и на всем отрезке производная функции не меняет знак. Кроме того, для методов хорд и касательных, а также комбинированного метода обязательно требуется, чтобы на данном отрезке первая и вторая производные функции не меняли свой знак (не обращались в ноль).

2. В методе деления отрезка пополам определяется средняя точка c отрезка [a,b] и из двух отрезков [a,c] и [c,b] выбирается тот, на концах которого функция F(x) имеет разные знаки. К выбранному отрезку применяется та же процедура. Процесс деления отрезков прекращается, когда длина очередного отрезка станет меньше требуемой точности eps1; за корень уравнения можно принять любую точку этого отрезка.

В остальных трех методах следует различать два случая:

случай 1 – первая и вторая производные функции F(x) имеют одинаковые знаки ( F'(x) F"(x) > 0 );

случай 2 – эти производные имеют разные знаки. ( F'(x) F"(x) < 0 ).

В методе хорд точки (a, F(a)) и (b, F(b)) кривой y=F(x) соединяются прямой линией и определяется точка пересечения этой линии с осью абсцисс:

c = (a F(b) – b F(a)) / (F(b) – F(a)) ( уравнение прямой )

Далее выбирается отрезок [c,b] в случае 1 или отрезок [a,c] в случае 2 и к нему применяется та же процедура. Тем самым происходит постепенное приближение к искомому корню слева ( в случае 1 ) или справа ( в случае 2 ).

В методе касательных проводится касательная к кривой y=F(x) в точке(b, F(b)) в случае 1 или в точке (a,F(a)) в случае 2 и определяется точка c пересечения этой касательной с осью абсцисс:

c=d-F(d)/F'(d), ( уравнение касательной )

где d=b в случае 1 и d=a в случае 2. Далее проводится касательная к кривой в точке (c, F(c)) и процедура повторяется. Тем самым происходит приближение к искомому корню справа (в случае 1) или слева (в случае 2).

В методах хорд и касательных можно использовать следующий критерий завершения процесса приближения к корню. Если приближение «идет» слева, то на очередном шаге надо сравнить величины F(c) и F(c+eps): если они одного знака, то процесс продолжается, иначе на отрезке [c,c+eps] имеется корень и потому процесс завершается. При приближении справа надо проверять знаки F(c–eps) и F(c).

В комбинированном методе одновременно применяется метод хорд и метод касательных, в связи с чем приближение к корню происходит с двух сторон. Критерий окончания – длина очередного отрезка меньше eps.

3. При использовании метода хорд, метода касательных или комбинированного метода процедура root должна самостоятельно распознавать, какой из двух случаев, указанных в п. 2, имеет место при текущем обращении к ней. Вместо проверки знаков первой и второй производных, можно сделать проверку двух других условий:

• функция возрастает или убывает;

• график функции расположен выше хорды или ниже.

Поскольку производные F'(x) и F"(x) на отрезке [a,b] не меняют знака (это было требованием к выбору отрезка для применимости метода), то для проверки первого условия достаточно сравнить F(a) с 0 : при F(a)<0 функция возрастает, иначе убывает. Для проверки же второго условия надо сравнить в какой-то внутренней точке отрезка значения функции и хорды; например, если взять среднюю точку (a+b)/2 отрезка, то соотношение F((a+b)/2) > (F(a)+F(b))/2 означает, что график функции расположен выше хорды ( или, по-другому, если F(c)>0, где (с,0) – точка пересечения хорды с осью абсцисс, то график функции расположен выше хорды, иначе – ниже ).

Выводы.

Если функция возрастает (F(a)<0) и ее график расположен ниже хорды (F(c)<0) ( см. рис1_а ), или если функция убывает (F(a)>0) и ее график расположен выше хорды (F(c)>0) ( см. рис1_б ), то имеет место случай_1: F(a)F(c)>0 имеют одинаковые знаки.

Если функция возрастает (F(a)<0) и ее график расположен выше хорды (F(c)>0) ( см. рис2_а ), или если функция убывает (F(a)>0) и ее график расположен ниже хорды (F(c)<0) ( см. рис2_б ), то имеет место случай_2: F(a)F(c)>0 имеют разные знаки.

F'(x) F"(x) > 0

Случай 1: F(a)F(c) > 0

F'(x) > 0 F'(x) < 0

F(a) < 0 возрастает F(a) > 0 убывает

F"(x) > 0 F”(x) < 0

F(c) < 0 ниже хорды F(c) > 0 выше хорды

рис1_а рис1_б

Для метода хорд (секущих) приближение к корню «идет» слева и на очередном шаге надо сравнить величины F(c) и F(c+eps): если они одного знака, то процесс продолжается, иначе на отрезке [c, c+eps] имеется корень и потому процесс завершается.

Для метода касательных (Ньютона) неподвижный конец отрезка a, потому в формуле d=b. Приближение к корню «идет» справа и надо проверять знаки F(c’– eps) и F(c’).

F'(x) F"(x) < 0

Случай 2: F(a)F(c) < 0

F'(x) > 0 F'(x) < 0

F(a) < 0 возрастает F(a) > 0 убывает

F"(x) < 0 F”(x) > 0

F(c) > 0 выше хорды F(c) < 0 ниже хорды

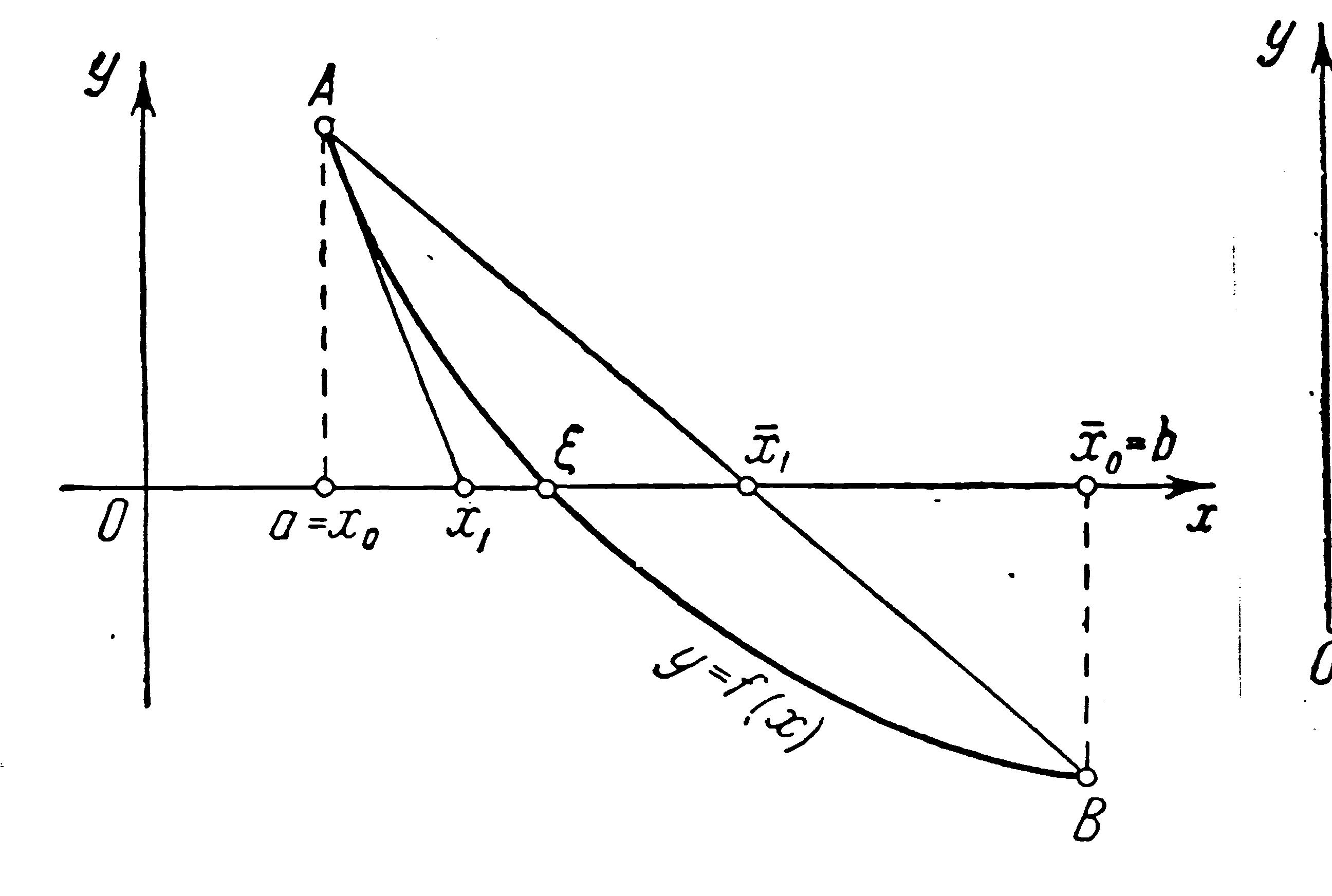
рис2_а рис2_б

Для метода хорд (секущих) приближение к корню «идет» справа и на очередном шаге надо сравнить величины F(c-eps) и F(c): если они одного знака, то процесс продолжается, иначе на отрезке [c, c–eps] имеется корень и потому процесс завершается.

Для метода касательных (Ньютона) неподвижный конец отрезка b, потому в формуле d=a. Приближение к корню «идет» слева и надо проверять знаки F(c’) и F(c’+eps).

4. Квадратурные формулы для приближенного вычисления интеграла I от функции F(x) на отрезке [a,b] имеют следующий вид (n - число разбиений отрезка [a,b]):

Формула прямоугольников:

I  I_n = h (F₀+F₁+...+F_n–1), где F_i = F(a+(i+0.5)h), h=(b-a)/n, i=0..n-1

Формула трапеций:

I  I_n = h (0.5F₀+F₁+F₂+...+F_n–1+0.5F_n), где F_i = F(a+ih), h=(b-a)/n, i=0..n

Формула парабол или Симпсона ( n – четное! ):

I  I_n = h/3*(F₀+4F₁+2F₂+4F₃+...+4F_n-3+2F_n-2+4F_n-1+F_n), где F_i = F(a+ih), h=(b-a)/n, i=0..n

5. Для обеспечения требуемой точности eps при приближенном вычислении интеграла I по квадратурной формуле нужно подобрать соответствующее число n разбиений отрезка интегрирования. Известны формулы, выражающие n через eps, но в эти формулы входят производные подынтегральной функции, что неудобно на прак­тике. Поэтому для достижения требуемой точности обычно используется следующий метод: берется некоторое начальное число разбиений n₀ (например, 8 или 16 ) и последовательно вычисляются значения I_n при n, равном 2n₀, 4n₀, 8n₀ и т.д. Известно правило Рунге | I – I_n |  p | I_n – I_2n |

(для формул прямоугольников и трапеций p=1/3, для формулы Симпсона p=1/15). Согласно этому правилу, когда на очередном шаге величина p|I_n-I_2n| окажется меньше eps, в качестве приближенного значения для I можно взять I_n , или лучше I_2n . [2] c230.

6 . При реализации функции integral следует учитывать, что в формулах трапеций и Симпсона в сумму I_2n входят значения F_i, вычисленные ранее для суммы I_n, поэтому их не следует перевычислять заново.

Пояснения к формуле Симпсона.

I_n = h/3*(F₀+4F₁+2F₂+4F₃+ ... +2F_n-2+4F_n-1+F_n) = = h/3* S

S = S0 + 4*S1 + 2*S2

S0 = F₀+ F_n = F(a)+F(b) S0 - неизменная величина

S1 = F₁+F₃+ ... +F_n-1

S2 = F₂+ ... +F_n-2

S2_new:=S1+S2

S1_new:={вычислить}

Пояснения к формуле трапеций.

I_n = h (0.5F₀+F₁+F₂+...+F_n–1+0.5F_n) = h ( S0 + Sm ) { S0=0.5F₀+0.5F_n ; Sm =ΣS_i } = h* S

Дальше, S = S + S1_new – надо “довычислить” только новые нечетные точки.

7. В процедуре root и функции integral используются параметры-функции ( f, g и др.). В языке Турбо Паскаль такие параметры описываются следующим образом.

В разделе типов необходимо описать т.н. функциональный тип:

type TF = function ( x : real) : real;

(вместо TF и x можно использовать любые другие имена), в который автоматически включаются все описанные в программе вещественные функции от одного веществен-ного аргумента, а затем имя данного типа нужно указать в спецификации формального параметра-функции, например:

procedure root ( f, g : TF; a, b, eps1 : real; var x : real );

При обращении же к процедуре root или функции integral указываются, как обычно, имена фактических функций (не стандартных!), например:

root( f1, f2, -0.1, 3.5, 0.0001, x12 );

Что касается самих фактических функций (f1, f2 и др.), то перед их описанием необходимо разместить директиву {$F+} транслятору:

{$F+}

function f1 ( x : real ): real; begin f1:=ln(x) end;

function f2 ( x : real ): real; begin f2:=2*x+14 end; . . .

8. { Программа для изучения поведения разности функций и ее производных

( на примере корня x13 var05 }

program F ( input, output, ff );

const n=10; a13=–1.999; b13=–1; {отрезок поиска корня f1=f3}

type func = function (x:real):real;

var ff: text;

{$F+}

Function f1(x: real):real;

begin f1:=0.35*x*x-0.95*x+2.7; end;

{ f1p, f1pp }

Function f2(x: real):real;

begin f2:=exp(x*ln(3))+1; end;

Function f3(x: real):real;

begin f3:=1/(x+2); end;

{ f3p, f3pp }

procedure PR (a,b:real; n:integer; fun1,fun2:func; c:char);

var h,x,y:real; i:integer;

begin

h:=(b–a)/n; x:=a–h;

writeln(ff);

writeln(ff,' X Y=(f1–f3)',c);

for i:=0 to n do

begin

x:=x+h ; y:=fun1(x)–fun2(x); writeln (ff,x:10:4,' ',y:10:4);

end;

end;{ PR }

BEGIN

writeln; writeln('Начало работы');

Assign( ff, 'res_05.pas' );

Rewrite(ff);

writeln(ff,' var_05');

PR(a13,b13, n, F1, F3, ' ');

{

PR(a13,b13,n, F1p, F3p, '''');

PR(a13,b13,n, F1pp,F3pp,'"');

}

Close(ff);

writeln('Конец работы'); writeln

END.

var_05 исходный отрезок поиска корня x13 a13=–1.999; b13=–1;

X Y=(f1–f3)

-1.9990 -994.0024

-1.8991 -4.1444 на отрезке [ -1.8991,

-1.7992 +0.5622 смена знака функции F=f1–f3 -1.7992 ]

-1.6993 1.9994

-1.5994 2.6185

-1.4995 2.9135

-1.3996 3.0497

-1.2997 3.0980

-1.1998 3.0940

-1.0999 3.0573

-1.0000 3.0000

на новом отрезке [-1.8991, -1.7992 ] ( добавив производные ) выбираем окончательный отрезок применимости метода

ОТЧЕТ ПО ЗАДАНИЮ N1

ЯЗЫК ПАСКАЛЬ. ВЫЧИСЛЕНИЕ КОРНЕЙ УРАВНЕНИЙ И ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

.............................................................

кем выполнено дата получения варианта

.............................................................

дата представления отчета подпись преподавателя, оценка