5. Оценить прогноз объема выпуска продукции, если прогнозные значения факторов составляют 75% от их максимальных значений.

Уравнение регрессии: У = 17243,98+0,62Х2

Х2 max = 1974472

Уmax= 17243,98+0,62*1974472 = 1 241 416,62

Уmax(75%) =17243,98+0,62*1974472*0,75 = 935373,46

Уmax(90%) =17243,98+0,62*1974472*0,9 = 1118999,356

Доверительные интервалы для отдельных значений результирующей переменной можно определить, рассчитав вначале для каждого уровня ошибки моделирования по формуле

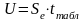
= 23 264,62

t_табл(0,05;15)= 2,13

t_табл(0,1;15)= 1,75

U(0,05) = 23 264,62*2,13 = 49553,64

U(0,1) = 23 264,62*1,75 = 40713,085

Затем определяется сам доверительный интервал:

нижняя граница – ,

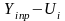верхняя граница – ,

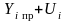где 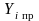– i-ый уровень предсказанного значения результата

Объем выпуска продукции при максимальных значениях фактора Х2.

Уmax=	1 241 416,62
U(0,05) =	49553,64
У max-U(0,05)	У max+U(0,05)
1191862,98	1290970,26
У max =	1 241 416,62
U(0,1) =	40713,085
У max-U(0,01)	У max+U(0,01)
1200703,535	1282129,705

Прогноз объема выпуска продукции, если прогнозные значения фактора составляют 75% от их максимальных значений.

Уmax(75%)=	935373,46
U(0,05) =	49553,64
Уmax(75%)-U(0,05)	Уmax(75%)+U(0,05)
885819,82	984927,1
Уmax(75%)=	935373,46
U(0,1) =	40713,085
Уmax(75%)-U(0,1)	Уmax(75%)+U(0,1)
894660,375	976086,545

Прогноз объема выпуска продукции, если прогнозные значения фактора составляют 90% от их максимальных значений.

Уmax(90%) =	1118999,356
U(0,05) =	49553,64
Уmax(90%)-U(0,05)	Уmax(90%)+U(0,05)
1069445,716	1168552,996
Уmax(90%) =	1118999,356
U(0,1) =	40713,085
Уmax(90%)-U(0,1)	Уmax(90%)+U(0,1)
1078286,271	1159712,441