3. Оценить статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента

1. Оценим статистическую значимость уравнения регрессии с помощью критерия Фишера. Расчетное значение F-критерия Фишера можно найти в регрессионном анализе (рисунок 5).

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	1,32E+12	1,32E+12	2447,317	4,94E-18
Остаток	15	8,12E+09	5,41E+08
Итого	16	1,33E+12

Рисунок 5. Фрагмент регрессионного анализа для однофакторной модели

F_табл(0,05;1;17-1-1=15) = 4,54

Так как F>F_табл, то уравнение однофакторной регрессии статистически значимо на 95% уровне значимости. Таким образом, связь У с включенным в модель фактором существенна.

2. Коэффициент уравнения регрессии признается значимым, если наблюдаемое значение t-статистики Стьюдента для этого коэффициента больше, чем критическое табличное значение статистики Стьюдента (для заданного уровня значимости).

	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	17243,98	6178,659	2,790894
X2	0,618526	0,012503	49,47036

Рисунок 6. Фрагмент регрессионного анализа для однофакторной модели

t_табл(0,05;17-1-1=15)= 2,13

Фактические значения t-критериев сравниваются с табличным значением при степенях свободы n-k-1 = 17-1-1=15 и уровне значимости α=0,05.

Фактор Х2 статистически значим (_tнабл > _tтабл).

4. Построить уравнение регрессии со статистически значимыми факторами. Оценить качество уравнения регрессии с помощью коэффициента детерминации r2. Оценить точность построенной модели.

Уравнение регрессии: У = 17243,98+0,62Х2

Качество уравнения регрессии оценивается коэффициентом детерминации R².

Регрессионная статистика
Множественный R	0,996949
R-квадрат	0,993908
Нормированный R-квадрат	0,993502
Стандартная ошибка	23264,62
Наблюдения	17

Рисунок 7. Фрагмент регрессионного анализа для однофакторной модели

Величина R² = 0,993908 означает, что фактором У (объем выпуска продукции) можно объяснить 99,3% вариации (разброса) объема выпуска продукции.

Уровень точности модели характеризует степень отклонения в среднем фактических значений результативной переменной У от ее значений, полученных по модели регрессии (предсказанных). Для оценки уровня точности используются различные ошибки: средняя относительная, стандартная и другие.

Cтандартная ошибка модели выводится в первой таблице «Регрессионная статистика» (рис. 8) отчета по регрессионному анализу.

Регрессионная статистика
Множественный R	0,996949
R-квадрат	0,993908
Нормированный R-квадрат	0,993502
Стандартная ошибка	23264,62
Наблюдения	17

Рисунок 8. Фрагмент регрессионного анализа для однофакторной модели

Точность модели тем лучше, чем меньше ее стандартная ошибка (это же имеет место и при использовании для оценки уровня точности других видов ошибок). Однако, понятие «чем меньше» является относительным и зависит от порядка чисел, представляющих данные задачи. Поэтому модель считается точной, если стандартная ошибка модели 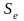меньше стандартной ошибки (среднеквадратического отклонения) результативного признака Y 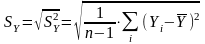. Стандартную ошибку легко найти в Excel с помощью статистической функции СТАНДОТКЛОН.

В данном случае стандартная ошибка модели равна 23 264,62, а среднеквадратическое отклонение (или стандартная ошибка) фактора Sу =288 607,7

Так как <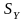 , то трехфакторная модель регрессии является точной.