Построить матрицу парных коэффициентов корреляции. Проверить наличие мультиколлинеарности. Обосновать отбор факторов в модель
В таблице 2 представлена матрица коэффициентов парной корреляции для всех переменных, участвующих в рассмотрении. Матрица получена с помощью инструмента Корреляция из пакета Анализ данных в Excel.
Таблица 2. Матрица коэффициентов парной корреляции
|
Y |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
Y |
1 |
|
|
|
|
|
|
X1 |
0,995634 |
1 |
|
|
|
|
|
X2 |
0,996949 |
0,994947 |
1 |
|
|
|
|
X3 |
-0,25446 |
-0,27074 |
-0,26264 |
1 |
|
|
|
X4 |
0,12291 |
0,07251 |
0,107572 |
0,248622 |
1 |
|
|
X5 |
0,222946 |
0,166919 |
0,219914 |
-0,07573 |
0,671386 |
1 |
|
X6 |
0,067685 |
-0,00273 |
0,041955 |
-0,28755 |
0,366382 |
0,600899 |
1 |
Визуальный анализ матрицы позволяет установить:
У имеет довольно высокие парные корреляции с переменными Х1, Х2 (>0,5) и низкие с переменными Х3,Х4,Х5,Х6 (<0,5);
Переменные анализа Х1, Х2 демонстрируют довольно высокие парные корреляции, что обуславливает необходимость проверки факторов на наличие между ними мультиколлинеарности. Тем более, что одним из условий классической регрессионной модели является предположение о независимости объясняющих переменных.
Для выявления мультиколлинеарности факторов выполним тест Фаррара-Глоубера по факторам Х1,Х2,Х3,Х4,Х5,Х6.
Проверка теста Фаррара-Глоубера на мультиколлинеарность факторов включает несколько этапов.
Проверка наличия мультиколлинеарности всего массива переменных.
Одним из условий классической регрессионной модели является предположение о независимости объясняющих переменных. Для выявления мультиколлинеарности между факторами вычисляется матрица межфакторных корреляций R с помощью Пакета анализа данных (таблица 3).
Таблица 3. Матрица межфакторных корреляций R
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X1 |
1 |
0,994947 |
-0,27074 |
0,07251 |
0,166919 |
-0,00273 |
X2 |
0,994947 |
1 |
-0,26264 |
0,107572 |
0,219914 |
0,041955 |
X3 |
-0,27074 |
-0,26264 |
1 |
0,248622 |
-0,07573 |
-0,28755 |
X4 |
0,07251 |
0,107572 |
0,248622 |
1 |
0,671386 |
0,366382 |
X5 |
0,166919 |
0,219914 |
-0,07573 |
0,671386 |
1 |
0,600899 |
X6 |
-0,00273 |
0,041955 |
-0,28755 |
0,366382 |
0,600899 |
1 |
Между факторами Х1 и Х2, Х5 и Х4, Х6 и Х5 наблюдается сильная зависимость (>0,5).
Определитель det (R) = 0,001488 вычисляется с помощью функции МОПРЕД. Определитель матрицы R стремится к нулю, что позволяет сделать предположение об общей мультиколлинеарности факторов.
Проверка наличия мультиколлинеарности каждой переменной с другими переменными:
Вычислим обратную матрицу R-1 с помощью функции Excel МОБР (таблица 4):
Таблица 4. Обратная матрица R-1
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X1 |
150,1209 |
-149,95 |
3,415228 |
-1,70527 |
6,775768 |
4,236465 |
X2 |
-149,95 |
150,9583 |
-3,00988 |
1,591549 |
-7,10952 |
-3,91954 |
X3 |
3,415228 |
-3,00988 |
1,541199 |
-0,76909 |
0,325241 |
0,665121 |
X4 |
-1,70527 |
1,591549 |
-0,76909 |
2,218969 |
-1,4854 |
-0,213 |
X5 |
6,775768 |
-7,10952 |
0,325241 |
-1,4854 |
2,943718 |
-0,81434 |
X6 |
4,236465 |
-3,91954 |
0,665121 |
-0,213 |
-0,81434 |
1,934647 |
Вычисление F-критериев
,
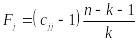где
–
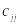диагональные элементы матрицы
,
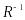n=17,
k
= 6 (таблица 5).
Таблица 5. Значения F-критериев
F1 (Х1) |
F2 (Х2) |
F3 (Х3) |
F4 (Х4) |
F5 (Х5) |
F6 (Х6) |
89,29396 |
89,79536 |
0,324071 |
0,729921 |
1,163903 |
0,559669 |
Фактические значения F-критериев сравниваются с табличным значением Fтабл= 3,21 (FРАСПОБР(0,05;6;10)) при 1= 6 и 2 = n - k – 1=17-6-1=10 степенях свободы и уровне значимости α=0,05, где k – количество факторов.
Значения F-критериев для факторов Х1 и Х2 больше табличного, что свидетельствует о наличии мультиколлинеарности между данными факторами. Меньше всего влияет на общую мультиколлинеарность факторов фактор Х3.
Проверка наличия мультиколлинеарности каждой пары переменных
Вычислим частные коэффициенты корреляции по формуле
,
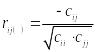где
–
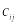элементы матрицы
(таблица
6)
Таблица
6. Матрица
коэффициентов частных корреляций
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X1 |
|
|
|
|
|
|
X2 |
0,996086 |
|
|
|
|
|
X3 |
-0,22453 |
0,197329 |
|
|
|
|
X4 |
0,093432 |
-0,08696 |
0,415882 |
|
|
|
X5 |
-0,32232 |
0,337259 |
-0,1527 |
0,581191 |
|
|
X6 |
-0,24859 |
0,229354 |
-0,38519 |
0,102801 |
0,341239 |
|
Вычисление t-критериев по формуле
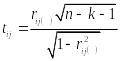(таблица
7)
n - число данных = 17
K - число факторов = 6
Таблица 7. t-критерии для коэффициентов частной корреляции
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X1 |
|
|
|
|
|
|
X2 |
35,6355 |
|
|
|
|
|
X3 |
-0,72862 |
0,636526 |
|
|
|
|
X4 |
0,296756 |
-0,27604 |
1,446126 |
|
|
|
X5 |
-1,07674 |
1,13288 |
-0,4886 |
2,258495 |
|
|
X6 |
-0,81158 |
0,745143 |
-1,31991 |
0,326817 |
1,147999 |
|
tтабл = СТЬЮДРАСПОБР(0,05;10) = 2,23
Фактические значения t-критериев сравниваются с табличным значением при степенях свободы n-k-1 = 17-6-1=10 и уровне значимости α=0,05;
t21 > tтабл
t54 > tтабл
Из таблиц 6 и 7 видно, что две пары факторов X1 и Х2, Х4 и Х5 имеют высокую статистически значимую частную корреляцию, то есть являются мультиколлинеарными. Для того чтобы избавиться от мультиколлинеарности, можно исключить одну из переменных коллинеарной пары. В паре Х1 и Х2 оставляем Х2, в паре Х4 и Х5 оставляем Х5.
Таким образом, в результате проверки теста Фаррара-Глоубера остаются факторы: Х2, Х3, Х5, Х6.
Завершая процедуры корреляционного анализа, целесообразно посмотреть частные корреляции выбранных факторов с результатом Y.
Построим матрицу парных коэффициентов корреляции, исходя из данных таблицы 8.
Таблица 8. Данные выпуска продукции с отобранными факторами Х2, Х3, Х5, Х6.
№ наблю-дения |
Y |
X2 |
X3 |
X5 |
X6 |
1 |
32900 |
16144 |
39,5 |
3,2 |
36354 |
2 |
203456 |
336472 |
46,4 |
20,4 |
23486 |
3 |
41138 |
39208 |
43,7 |
9,5 |
20866 |
4 |
57342 |
63273 |
35,7 |
34,7 |
47318 |
5 |
27294 |
31271 |
41,8 |
17,9 |
17230 |
6 |
94552 |
86129 |
49,8 |
12,1 |
19025 |
7 |
28507 |
48461 |
44,1 |
18,9 |
18262 |
8 |
97788 |
138657 |
48,1 |
12,2 |
23360 |
9 |
101734 |
127570 |
47,6 |
8,1 |
15223 |
10 |
175322 |
208900 |
58,6 |
29,7 |
32920 |
11 |
2894 |
6922 |
70,4 |
5,3 |
5291 |
12 |
16649 |
8228 |
37,5 |
5,6 |
23125 |
13 |
19216 |
18894 |
62 |
12,3 |
20848 |
14 |
23684 |
27486 |
34,4 |
3,2 |
6713 |
15 |
1237132 |
1974472 |
35,4 |
19 |
22581 |
16 |
88569 |
162229 |
40,8 |
19,3 |
20522 |
17 |
162216 |
128731 |
48,1 |
12,4 |
26396 |
В последнем столбце таблицы 9 представлены значения t-критерия для столбца У.
Таблица 9. Матрица коэффициентов частной корреляции с результатом Y
|
Y |
X2 |
X3 |
X5 |
X6 |
t критерий (tтабл(0,05;11)= 2,200985 |
Y |
1 |
0,996949 |
-0,25446 |
0,222946 |
0,067685 |
|
X2 |
0,996949 |
1 |
-0,26264 |
0,219914 |
0,041955 |
44,31676 |
X3 |
-0,25446 |
-0,26264 |
1 |
-0,07573 |
-0,28755 |
0,916144 |
X5 |
0,222946 |
0,219914 |
-0,07573 |
1 |
0,600899 |
-0,88721 |
X6 |
0,067685 |
0,041955 |
-0,28755 |
0,600899 |
1 |
1,645749 |
Из таблицы 9 видно, что переменная Y имеет высокую и одновременно статистически значимую частную корреляцию с фактором Х2.