4. Рассчитать прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.

Уравнение регрессии: У = -9495,79+21,39 Х1+540,2393Х3

Уmax = -9495,79+21,39 Х1 max +540,2393Х3 max

Х1max = 8212

Х3 max = 87,2

Уmax = -9495,79+21,39 *8212 +540,2393*87,2 = 213267,757

Уmax(80%) = -9495,79+21,39 *8212*0,8 +540,2393*87,2*0,8 =168715,0476

Уmax(90%) = -9495,79+21,39 *8212*0,9 +540,2393*87,2 *0,9 =190991,4023

5. Рассчитать ошибки и доверительный интервал прогноза для уровня значимости 5% или 10% ( = 0,05; = 0,1). Для всех вариантов.

Уровень точности модели характеризует степень отклонения в среднем фактических значений результативной переменной У от ее значений, полученных по модели регрессии (предсказанных). Для оценки уровня точности используются различные ошибки: средняя относительная, стандартная и другие.

Cтандартная ошибка модели 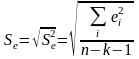выводится в первой таблице «Регрессионная статистика» отчета по регрессионному анализу. Для двухфакторной модели эта таблица представлена на рисунке 8.

Регрессионная статистика
Множественный R	0,949689
R-квадрат	0,90191
Нормированный R-квадрат	0,847538
Стандартная ошибка	16438,27
Наблюдения	25

Рисунок 8. Фрагмент регрессионного анализа для двухфакторной модели

Точность модели тем лучше, чем меньше ее стандартная ошибка (это же имеет место и при использовании для оценки уровня точности других видов ошибок). Однако, понятие «чем меньше» является относительным и зависит от порядка чисел, представляющих данные задачи. Поэтому модель считается точной, если стандартная ошибка модели 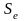меньше стандартной ошибки (среднеквадратического отклонения) результативного признака Y 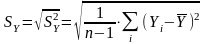. Стандартную ошибку легко найти в Excel с помощью статистической функции СТАНДОТКЛОН.

В данном случае стандартная ошибка модели равна 16438,265, а среднеквадратическое отклонение (или стандартная ошибка) фактора S_у = 50251,44.

Так как < , то трехфакторная модель регрессии является точной.

Доверительные интервалы для отдельных значений результирующей переменной можно определить, рассчитав вначале для каждого уровня ошибки моделирования по формуле

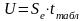
= 16438,265

t_табл(0,05;22)= 2,07

t_табл(0,1;22)=1,71

U(0,05) = 16438,265 * 2,07 = 34090,87

U(0,1)= 16438,265 * 1,71 = 28226,87

Затем определяется сам доверительный интервал:

нижняя граница – ,

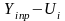верхняя граница – ,

где 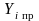– i-ый уровень предсказанного значения результата.

Объем выпуска продукции при максимальных значениях факторов Х1,Х3.

Уmax=	213267,757
U(0,05)=	34090,87491
Уmax-U(0,05)	Уmax+U(0,05)
179176,8821	247358,6319
Уmax=	213267,757
U(0,1)=	28226,87363
Уmax-U(0,1)	Уmax+U(0,1)
185040,8834	241494,6306

Прогноз объема выпуска продукции, если прогнозные значения факторов составляют 80% от их максимальных значений.

Уmax(80%) =	168715,0476
U(0,05)=	34090,87491
Уmax(80%)-U(0,05)	Уmax(80%)+U(0,05)
134624,1727	202805,9225
Уmax(80%) =	168715,0476
U(0,1)=	28226,87363
Уmax(80%)-U(0,1)	Уmax(80%)+U(0,1)
140488,174	196941,9212

Прогноз объема выпуска продукции, если прогнозные значения факторов составляют 90% от их максимальных значений.

Уmax(90%) =	190991,4023
U(0,05)=	34090,87491
Уmax(90%)-U(0,05)	Уmax(90%)+U(0,05)
156900,5274	225082,2772
Уmax(90%) =	190991,4023
U(0,1)=	28226,87363
Уmax(90%)-U(0,1)	Уmax(90%)+U(0,1)
162764,5287	219218,2759