3. Привести график остатков. Проверить условие гомоскедастичности остатков.

Дисперсия остатков должна была гомоскедастичной. Это значит, что для каждого значения фактора х остатки Sj имеют одинаковую дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность.

При проверке предпосылки МНК о гомоскедастичности остатков в модели множественной регрессии следует вначале определить, по отношению к какому из факторов дисперсия остатков более всего нарушена. Это можно сделать в результате визуального исследования графиков остатков, построенных по каждому из факторов, включенных в модель. Та из объясняющих переменных, от которой больше зависит дисперсия случайных возмущений, и будет упорядочена по возрастанию фактических значений при проверке теста Голдфельда-Квандта.

Для двухфакторной модели графики остатков относительно каждого из двух факторов имеют вид, представленный на рисунке 3 (эти графики легко получить в отчете, который формируется в результате использования инструмента Регрессия в пакете Анализ данных).

Рисунок 3. Графики остатков по каждому из факторов двухфакторной модели

На каждой из диаграмм ярко выражена направленность в распределении остатков, то есть непостоянство их дисперсии. В таком случае предпосылку о гомоскедастичности остатков следует проверять дважды, каждый раз упорядочивая значения переменных по возрастанию одного из факторов. Начнем с фактора, который имеет самое большое значение t-статистики, то есть с фактора Х1 (t=9,985).

Основные этапы теста Голдфельда-Квандта:

1. Упорядочим переменные У, Х3 по мере возрастания переменной Х1, относительно которой есть подозрение на гетероскедастичность (в Excel для этого можно использовать команду Данные – Сортировка – По возрастанию Х1) (таблица 10).

Таблица 10. Данные, упорядоченные по возрастанию переменной Х1

№	Y	X1	X3
23	1878	77	0,6
3	3118	210	5,7
9	13425	459	33,5
20	18135	763	25,9
15	10201	802	14,9
19	32900	864	4,9
6	19216	940	27,6
12	14781	964	4,4
21	29589	1003	43,5
17	47064	1110	5,8
18	57342	1147	50,4
7	16567	1197	31,1
10	31163	1405	35,1
25	6896	1556	0,7
5	56262	1559	56,2
11	30109	1575	26,5
22	22604	1680	3,1
13	41138	1866	24,9
24	49378	2505	43,1
16	75282	2600	2,4
1	62240	2890	13,9
2	88569	4409	55,3
14	69202	4419	13,2
4	186256	5436	87,2
8	203456	8212	60,5

2. Уберем из середины упорядоченной совокупности С=1/4*n=1/4*25 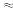6 значений. В результате получим две совокупности по ½*(25-6)=9(10) значений соответственно с малыми и большими значениями Х1.

Поскольку количество значении нечетное, одна совокупность будет состоять из 9 значений, другая – из 10 значений, соответственно с малыми и большими значениями Х1.

3. Для каждой совокупности в отдельности выполним регрессионный анализ (рисунок 4).

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	2	1,1E+09	5,52E+08	5,834366	0,032281
Остаток	7	6,62E+08	94565297
Итого	9	1,77E+09
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 90,0%	Верхние 90,0%
Y-пересечение	-2706,7	7553,437	-0,35834	0,730652	-20567,7	15154,34	-17017,3	11603,88
X1	32,35266	9,589633	3,373712	0,01186	9,676785	55,02854	14,18435	50,52098
X3	-91,765	226,2142	-0,40566	0,697109	-626,677	443,1467	-520,346	336,8157

Рисунок 4. Фрагмент регрессионного анализа двухфакторной модели для совокупности с меньшими значениями Х1

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	2	2,88E+10	1,44E+10	26,1608	0,001089
Остаток	6	3,3E+09	5,51E+08
Итого	8	3,21E+10
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 90,0%	Верхние 90,0%
Y-пересечение	-15308,8	16915,39	-0,90502	0,400334	-56699,2	26081,69	-48178,4	17560,87
X1	21,7183	5,35089	4,058821	0,006659	8,625146	34,81146	11,32056	32,11604
X3	649,2509	380,3578	1,706948	0,138703	-281,451	1579,953	-89,8529	1388,355

Рисунок 5. Фрагмент регрессионного анализа двухфакторной модели для совокупности с большими значениями Х1

4. Найдем отношение полученных остаточных сумм квадратов (в числителе должна быть большая сумма):

R = 3304797809,70635 / 661957076,479829 = 4,99246541

5. Вывод о наличии гомоскедастичности остатков делаем с помощью F-критерия Фишера с уровнем значимости 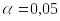и двумя одинаковыми степенями свободы k₁=k₂=(n-C-2*p)/2=(25-6-2*3)/2=6,5 (р – число параметров (коэффициентов) в уравнении регрессии):

F_табл(0,05;6,5;6,5)= 4,28

Так как F_набл> F_табл, то обнаруживается наличие гетероскедастичности в остатках модели по отношению к факторуХ1.

Проверим условие гомоскедастичности в остатках по фактору Х3, значение t-статистики которого составляет 3,098.

1. Упорядочим переменные У, Х1 по мере возрастания переменной Х3, относительно которой есть подозрение на гетероскедастичность.

Таблица 11. Данные, упорядоченные по возрастанию переменной Х3

№	Y	X1	X3
23	1878	77	0,6
25	6896	1556	0,7
16	75282	2600	2,4
22	22604	1680	3,1
12	14781	964	4,4
19	32900	864	4,9
3	3118	210	5,7
17	47064	1110	5,8
14	69202	4419	13,2
1	62240	2890	13,9
15	10201	802	14,9
13	41138	1866	24,9
20	18135	763	25,9
11	30109	1575	26,5
6	19216	940	27,6
7	16567	1197	31,1
9	13425	459	33,5
10	31163	1405	35,1
24	49378	2505	43,1
21	29589	1003	43,5
18	57342	1147	50,4
2	88569	4409	55,3
5	56262	1559	56,2
8	203456	8212	60,5
4	186256	5436	87,2

2. Уберем из середины упорядоченной совокупности С=1/4*n=1/4*25 6 значений. В результате получим две совокупности по ½*(25-6)=9(10) значений соответственно с малыми и большими значениями Х3.

Поскольку количество значении нечетное, одна совокупность будет состоять из 9 значений, другая – из 10 значений, соответственно с малыми и большими значениями Х3.

3. Для каждой совокупности в отдельности выполним регрессионный анализ (рисунок 6).

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	2	4,79E+09	2,39E+09	7,144193	0,020387
Остаток	7	2,34E+09	3,35E+08
Итого	9	7,13E+09
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 90,0%	Верхние 90,0%
Y-пересечение	4413,652	9891,968	0,446185	0,668939	-18977,1	27804,44	-14327,5	23154,76
X1	15,70137	6,192538	2,53553	0,038917	1,05834	30,34439	3,969116	27,43362
X3	636,1447	1780,984	0,357187	0,731477	-3575,21	4847,503	-2738,07	4010,359

Рисунок 6. Фрагмент регрессионного анализа двухфакторной модели для совокупности с меньшими значениями Х3

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	2	3,69E+10	1,84E+10	98,97575	2,55E-05
Остаток	6	1,12E+09	1,86E+08
Итого	8	3,8E+10
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 90,0%	Верхние 90,0%
Y-пересечение	-54666,6	17264,03	-3,1665	0,019404	-96910,2	-12423	-88213,7	-21119,5
X1	18,6394	2,511471	7,421706	0,000308	12,49405	24,78475	13,75916	23,51964
X3	1549,696	399,8266	3,875921	0,008209	571,3559	2528,037	772,7612	2326,632

Рисунок 7. Фрагмент регрессионного анализа двухфакторной модели для совокупности с большими значениями Х3

4. Найдем отношение полученных остаточных сумм квадратов (в числителе должна быть большая сумма):

R = 2344641318,98718 / 1117206090,03134 = 2,098665

5. Вывод о наличии гомоскедастичности остатков делаем с помощью F-критерия Фишера с уровнем значимости и двумя одинаковыми степенями свободы k₁=k₂=(n-C-2*p)/2=(25-6-2*3)/2=6,5 (здесь р – число параметров (коэффициентов) в уравнении регрессии):

(FРАСПОБР(0,05;6,5;6,5))

F_табл(0,05;6,5;6,5)= 4,283865714

Так как F_набл> F_табл, то обнаруживается наличие гетероскедастичности в остатках модели по отношению к факторуХ3.