Контрольные вопросы

1. Дайте определение термодинамической системы, окружающей среды. Всегда ли можно провести четкую границу системы и окружающей среды? В чем различие изолированной, адиабатной и закрытой систем?

2. Что означает словосочетание «гетерогенная система»? Что такое «фаза», «агрегатное состояние»?

3. Что означает «равновесное», «стационарное» состояние системы? Перечислите основные параметры состояния.

4. Сколько существует видов теплопереноса? В чем особенности каждого из них? Перечислите сложные виды теплопереноса.

5. Какова природа теплового излучения? Перечислите свойства электромагнитных волн. Объясните вывод закона Стефана-Больцмана.

6. Запишите уравнение энергетического баланса, если в системе происходит радиационно-конвективный теплообмен.

7. Температурное поле в изотропном твердом теле с теплопроводностью задается уравнением , и - постоянные величины. Запишите вектор плотности теплового потока.

Работа 1 (ММТП-001М)

ОПРЕДЕЛЕНИЕ ТЕПЛОПРОВОДНОСТИ ТВЕРДЫХ МАТЕРИАЛОВ МЕТОДОМ ПЛАСТИНЫ ПРИ ИМИТАЦИОННОМ МОДЕЛИРОВАНИИ ПРОЦЕССА ТЕПЛООБМЕНА

Цель работы - определить теплопроводность фторопласта методом плоского слоя в зависимости от температуры, определить влияние на температурное поле внутренних источников теплоты и термических контактных сопротивлений.

Введение

Исследование явления теплопроводности может быть сведено к изучению пространственно-временных изменений величин, характеризующих теплообмен. Совокупность значений температур во всех точках какого-то тела в данный момент времени t называется температурным полем этого тела. Температурное поле в декартовой системе координат задается уравнением вида

.

1.1

Совокупность точек тела, имеющих одинаковую температуру, составит изотермическую поверхность. Предел отношения изменения температуры DT к расстоянию по нормали между соответствующими изотермическими поверхностями при называется температурным градиентом :

.

1.2

Количественная оценка теплоты, проходящей внутри тела вследствие теплопроводности, базируется на основном законе теплопроводности Фурье:

, или ,

1.3

где величина l называется коэффициентом теплопроводности.

Для решения задач о нахождении теплопроводности обязательным является знание поля температур, то есть пространственно-временного распределения температуры в интересующей нас области. Такое распределение подчиняется основному дифференциальному уравнению теплопроводности Фурье-Кирхгофа, в основу вывода которого положен закон Фурье. Для нестационарного теплового режима в случае твердого тела с изотропными и однородными свойствами, при постоянной теплопроводности ) и при внутренних источниках теплоты уравнение Фурье-Кирхгофа для декартовой системы координат имеет вид

.

1.4

Здесь Т – температура [К]; t -время [с ]; a - коэффициент температуропроводности: a = l/С_р r, [ м²/с ]; l - теплопроводность [ Вт/(м К)]; С_р – удельная теплоемкость [ Дж/(кг К)] = 1 Дж/(кг К); r - плотность [ кг/м³]; q_v – объемное тепловыделение [ Вт/м³].

Теплопроводность реальных систем, как правило, зависит от температуры и уравнение (1.4) имеет вид

.

1.5

Для решения конкретных задач дифференциальное уравнение теплопроводности дополняется условиями однозначности. Условиями однозначности называют те дополнительные частные данные, которые характеризуют рассматриваемую задачу. Они включают в себя геометрические условия, характеризующие форму и размеры тела; физические условия, характеризующие физические свойства тела и окружающей среды; временные (начальные) условия, связанные с распределением температур в теле в начальный момент времени; граничные условия, характеризующие особенности протекания процессов теплообмена на границах тела.

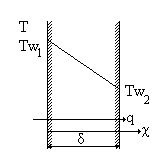
Применим дифференциальное уравнение теплопроводности в сочетании с условиями однозначности к задаче об одномерном температурном поле. Рассмотрим модель плоской стенки.

		Плоской называют стенку, толщина которой d значительно меньше двух других характерных размеров (ширины и длины). В этом случае можно пренебречь отводом теплоты через торцы стенки, считая, что тепловой поток направлен перпендикулярно большей поверхности пластины вдоль оси Х (рис.1.1). Таким образом, гео-
Рис. 1.1

метрическими условиями однозначности заданы форма и размеры стенки. Физические условия однозначности заключаются в том, что известен материал стенки и, следовательно, известно значение теплопроводности l. Будем считать, что материала стенки является изотропной и однородной величиной.

В данной лабораторной работе временные условия однозначности определены стационарным тепловым режимом, следовательно,

.

1.6

Сложилось три способа задания граничных условий в соответствии с тремя основными классами задач. При граничных условиях первого рода задано распределение температур на поверхности тела. В этом случае требуется определить величину плотности теплового потока. При граничных условиях второго рода известны величина плотности теплового потока и температура одной из поверхностей. И тогда возможно определить неизвестную температуру другой поверхности стенки. При граничных условиях третьего рода определяется величина плотности теплового потока, когда известны температуры сред, омывающих с разных сторон стенку, и коэффициенты теплоотдачи между поверхностями и средами. Этот случай описывает теплообмен, называемый теплопередачей.

В данной лабораторной работе будут обеспечены граничные условия первого рода. Для плоской стенки в стационарном режиме теплообмена температурное поле зависит только от одной координаты Х (рис.1.1) и тогда задача является пространственно одномерной, поскольку

.

1.7

Дифференциальное уравнение теплопроводности (1.4) при отсутствии объемного тепловыделения и при условии постоянства теплопроводности от температуры имеет вид

.

1.8

Закон распределения температур по толщине стенки при условии, что

п ри ;

при ;

найдется после двойного интегрирования уравнения (1.8).

.

1.9

Величина плотности теплового потока может быть определена как

.

1.10

Отношение l/d носит название тепловой проводимостью стенки, а обратная ей величина d/l =R называется термическим сопротивлением стенки.

Для определения значения теплопроводности по измеренным величинам можно использовать выражение

.

1.11

В этом случае полученное значение теплопроводности следует отнести к средней температуре .

Значение теплопроводности материала определяется экспериментально в стационарных условиях. Несмотря на методическую простоту, практическое осуществление сталкивается с трудностями создания одномерного температурного поля в исследуемых образцах и учете тепловых потерь. Метод связан со значительным временем выхода установки на стационарный тепловой режим. Имитационные установки позволяют избежать этих трудностей.

При исследовании теплопроводности материалов, обладающих низкой теплопроводностью (l< 2.3 Вт/(м К)), широкое распространение получил метод неограниченного плоского слоя, когда образцу исследуемого материала придается форма тонкой круглой или квадратной пластины. При выборе геометрических размеров исследуемых образцов с низкой теплопроводностью необходимо выполнять условие , где D – диаметр круглой пластины (или сторона квадрата), обеспечивающее одномерность температурного поля. Для устранения тепловых потерь с боковых поверхностей образца используют тепловую изоляцию или охранные электрические нагреватели. Описанный метод плоского слоя и используется в данной работе.

В работе требуется получить аналитическую зависимость теплопроводности от температуры l(T). Приближенно эту зависимость можно выразить в виде линейной функции

1.12

Задача состоит в определении коэффициентов l₀ и b. Для их нахождения необходимы результаты обработки, как минимум, двух экспериментов с разными температурными режимами. Для определения двух неизвестных l₀ и b по двум экспериментам используется система двух уравнений

.

Из решения этой системы уравнений получается

,

.

В работе проводятся три эксперимента, полученные значения l₀ и b необходимо усреднить.