Обработка результатов.

1. Для определения среднего по поверхности трубы коэффициента теплоотдачи используется формула Ньютона (3.5).

В рассматриваемых условиях опытов теплота Q, выделенная на экспериментальном участке в результате пропускания по нему электрического тока, отдается в окружающую среду как посредством естественной конвекции Q_к , так и посредством излучения Q_и . Поэтому теплота, отдаваемая поверхностью трубы посредством конвекции Q_к , определяется как разность между теплотой Q , выделяемой электрическим током и теплотой Q_и, отдаваемой посредством лучистого теплообмена, т.е.

.

Соответственно, плотность теплового потока q_w определится как , где S – площадь наружной поверхности трубы.

2. Определяется теплота, выделенная на экспериментальном участке в результате пропускания по нему электрического тока

[Вт],

где U – напряжение электрического тока, подаваемое на экспериментальный участок и измеряемое вольтметром в вольтах; R – электрическое сопротивление трубы:

, ,

где l – длина трубы, F - площадь поперечного кольцевого сечения (материала) трубы; d – наружный диаметр трубы; d₀ = d - 2d - внутренний диаметр трубы; r - удельное сопротивление материала трубы, для нержавеющей стали r определяется, в зависимости от температуры, как

[Ом·м]; ;

- средняя температура трубы; ( – значение измеряемых температур по контуру поперечного сечения трубы, n – количество измерений в сечении трубы).

3. Определяется теплота, отдаваемая поверхностью трубы в окружающее пространство посредством излучения согласно закону Стефана-Больцмана:

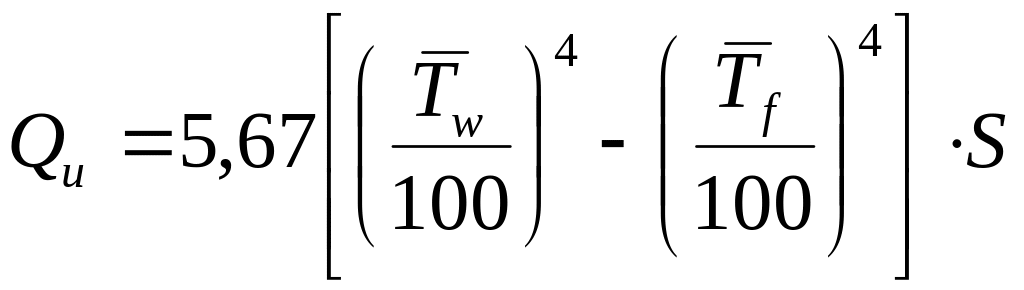[Вт].

Здесь e - степень черноты (e=0,2); - средняя по контуру поперечного сечения температура поверхности трубы, измеренная в кельвинах ( = +273[K]); Т_¦ -температура среды в кельвинах; S = pdl – площадь наружной поверхности трубы, [S] = 1 м², [Q_и] = 1 Вт.

4. Определяется плотность теплового потока на поверхности трубы, обусловленная теплообменом посредством естественной конвекции

.

5. Определяется среднее (по контуру поперечного сечения трубы) значение коэффициента теплоотдачи для каждого температурного режима по формуле Ньютона (3.5).

6. Определяются критерии подобия Nu_¦, Gr_¦, Pr_¦ :

, , .

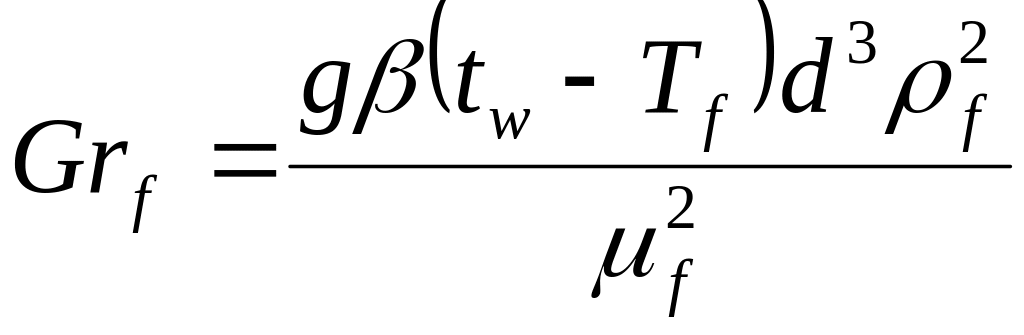Критерий Прандтля для воздуха можно принять Pr_¦ = 0,7; ускорение свободного падения; b_f = 1/Т_f – коэффициент объемного расширения; r_¦ - плотность воздуха, определяемая из уравнения состояния (Р₀ – давление окружающей среды в паскалях), – газовая постоянная воздуха; l_¦ , m_¦ - соответственно теплопроводность и динамическая вязкость воздуха, определяемые в зависимости от температуры среды Т_¦ согласно эмпирическим зависимостям

;

.

7. Результаты расчетов сводятся в таблицу 3.3.

Таблица 3.3.

№ режима	Q, Вт	Qи, Вт	qw, Вт/м2	, К	, Вт/(м2К)	Nu¦	(GrPr)¦	lgNu¦	Lg(GrPr)¦

8. В логарифмических координатах строится известная зависимость для среднего (по контуру поперечного сечения трубы) значения критерия Нуссельта (3.11). На зависимость наносятся соответствующие экспериментальные значения.