0. §2.5 Динамика твердого тела, закрепленного на оси.

Твердое тело, закрепленное на оси, обладает одной степенью свободы, то есть для определения его положения, достаточно одной независимой переменной, в качестве которой будем использовать угол Эйлера (1.2)

, ось Z совпадает с осью поворота.

Z

Y

X

- радиус траектории.

Пусть направлена вдоль Z.

Рассмотрим момент импульса твердого тела:

(1.2)

Найдем проекцию на ось Z:

Где ; - расстояние от точки i до оси вращения; - момент инерции твердого тела, относительно оси вращения Z.

Таким образом:

- сумма моментов внешних сил, действующих на твердое тело.

Мы рассмотрели случай, когда направлен вдоль оси Z, если направлен в другую сторону, то , а в общем случае .

Уравнение движения твердого тела с неподвижной осью будет:

0. §2.6 Кинетическая энергия вращающегося тела. Теорема Штейнера - Гюйгенса.

Рассмотрим твердое тело с неподвижной осью вращения. Его кинетическая энергия будет равна:

Момент инерции играет важную роль при описании движения твердого тела. Для определения момента инерции твердого тела удобно пользоваться теоремой Штейнера - Гюйгенса.

Пусть - момент инерции твердого тела, относительно произвольной оси Z, а - момент инерции относительно , параллельной и проходящей через центр масс твердого тела.

A

i

m

Y

Радиус- вектор центра масс в системе будет:

, так как центр масс лежит на оси и его координаты и равны.

Пример:

1) Момент инерции тонкого кольца:

2) Момент инерции диска:

§ 2.7. Динамика твердого тела с неподвижной точкой. Уравнение Эйлера.

Рассмотрим твердое тело с неподвижной точкой. Для описания движения такого тела необходимо 3 независимых переменных (так как у него 3 степени свободы). Для нахождения этих переменных нужно три скалярных уравнений. В качестве этих рассмотрим:

, где - сумма моментов внешних сил, действующих на тело.

i

Момент импульса твердого тела называется:

- квадрат расстояния от оси , до точки i.

Тогда, - момент инерции твердого тела относительно оси .

Переобозначим:

Точно так же:

Набор из девяти коэффициентов:

Называется тензором инерции твердого тела.

Диагональные элементы тензора – моменты инерции твердого тела, относительно соответствующих осей , которые жестко связаны с твердым телом.

Положение этих осей в твердом теле можно выбирать произвольно. При каждом новом выборе будут меняться коэфицентов тензора инерции.

Из математики известно, что существуют такие оси , при которых тензор инерции принимает диагональный вид ( ). Такие оси называются осями инерции, а диагональные элементы тензора называются главными моментами инерции.

Пусть оси совпадают с осями инерции твердого тела, тогда:

Отсюда следует:

; .

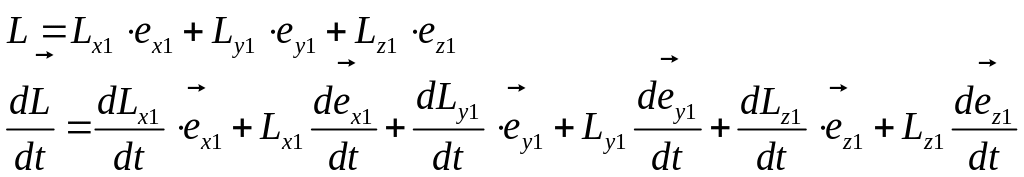
Полученные уравнения называются уравнениями Эйлера и полностью описывают движение твердого тела с неподвижной точкой.