Глава II Магнитостатика.

§2.1 Силы Лоренца и Ампера

Из опыта известно, что кроме электрической силы действует на заряд …..????

Для характеристики этой силы, вводят вектор магнитной индукции, обозначается в [Тл] , который характеризует магнитное поле, таким образом, что сила магнитного поля будет:

Общая сила действует на заряд:

– сила Лоренца.

Рассмотрим бесконечно маленький участок dl тонкого проводника, по которому течёт ток с постоянной по сечению с плотностью j, тогда I = Js

Пусть проводник находиться в магнитном поле

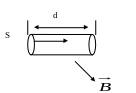
, так как длина проводника мала, то значение вектора B во всех точках одинакова.

Если ток в проводнике постоянен, то скорости всех зарядов одинаковые. Тогда на каждый заряд проводника будет действовать сила со стороны магнитного поля: .

Все силы одинаковы по величине и направлению, значит ,N – число зарядов внутри участка проводника.

Если концентрация зарядов проводника n , то , тогда

J – направлен параллельно стенкам проводника, величина которого равна длине проводника, а направление совпадает с направлением тока в проводнике

– сила Ампера

§2.2 Магнитное поле прямого проводника с током.

Рассмотрим проводник, по которому течет ток 1. Будем считать, что плотность положительных и отрицательных зарядов отрицательна

, общая плоскость проводника = 0

Для простоты предположим, что скорости «+» и «-» зарядов одинаковы.

- Линейная плотность заряда проводника.

Рассмотрим 2.И.С.О.:

Неподвижную х, у и подвижную х1 у1…….

* * *

Определим линейную плотность проводника, который движется со скоростью u

Плотность «+» в системе x₁y₁

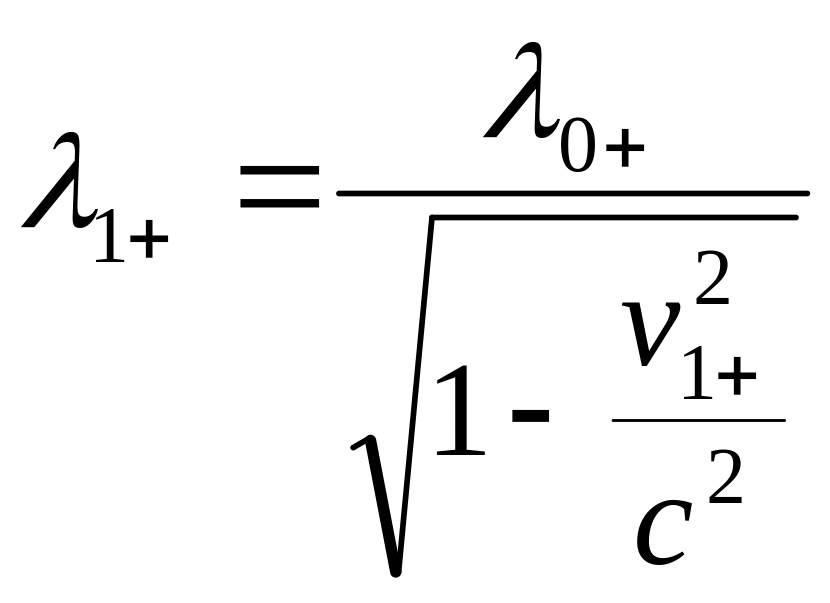
- плотность неподвижного проводника

-линейная плотность проводника

-скорость «+» зарядов в системе х₁ у₂

Линейная плотность «+» зарядов:

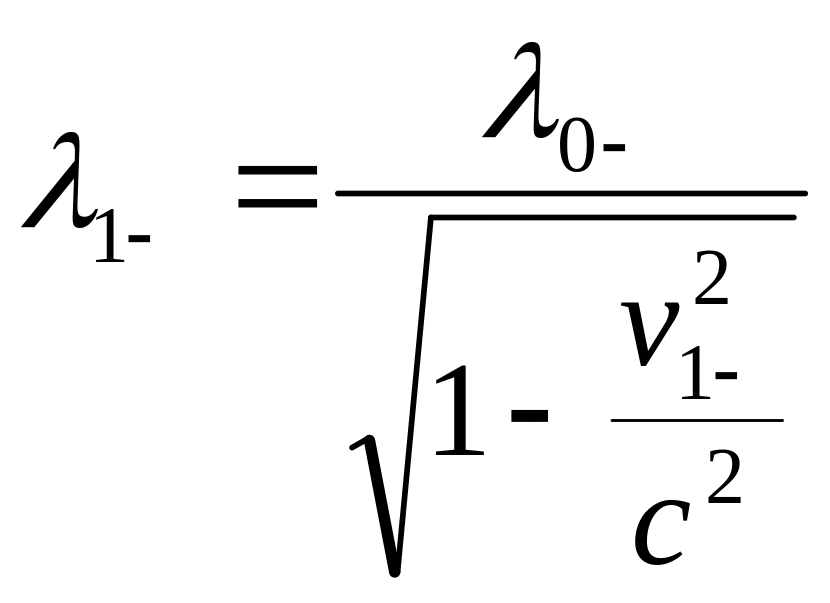
-скорость отрицательных зарядов

Линейная плотность «+» зарядов в системе х, у

Плотность «-» зарядов

Точка О в системе х₁ у₁ общая линейная плотность заряда будет:

В системе х₁ у₁, проводник оказывается заряжен с линейной плотностью , это значит, что в этой системе вокруг проводника будет электрическое поле с напряжением .

(см. 2.2)

Так как в системе заряд q неподвижен, то магнитное поле на тело не действует.

Как было показано в 3.6 в системе х, у на заряд q будет действовать сила вдоль оси у

Сравнивая полученные выражения с формулой , находим, что вектор магнитной индукции в системе х, у направлен по касательной окружности радиуса R и равен:

R

ПРОПУЩЕНО ПРИДУ К ТЕ ПРИДЁТСЯ ДОПЕЧАТАТЬ

2.3 Закон полного тока. Теорема о циркуляции.

------

* * *

Вычислим циркуляцию произвольного вектора с по замкнутому контуру в виде прямоугольника с бесконечно малыми сторонами и

y

y+dx

Будем считать, что величина dx и dy настолько малы, что значение вектора с на каждой стороне контура во всех точках одинаково.

(1)

так как dS направлена вдоль оси z, то ….

Рассмотрим циркуляцию вектора с по произвольно замкнутому контуру. Для этого разобьем поверхность ограниченную контуром на бесконечно малом. ds. Вычислим циркуляцию вектора с по каждому моменту прямоугольника площадью ds по формуле , и затем сложим циркуляции по всем внутренним сторонам в сумме дадут 0 и останется только циркуляция по тем сторонам прямоугольника, которые совпадут с контуром.

- т. Стокса

Теорема Стокса позволяет выяснить физический смысл ротора вектора. Для этого в качестве примера рассмотрим вектор скорости жидкости в водоёме.

Если движения жидкости в водоёме ламинарное (без турбулентности), то циркуляции вектора по любому замкнутому контуру будет = 0

т. О ротор с можно рассматривать, как поверхностную плотность источников вихревого движения поля с. Рисунок

Если ротор с не = 0, то поле называется вихревым.

Потенциальным полем мы называем поле, которое можно представить в виде градиента скалярной функции , заметим ротор любого градиента всегда = 0.

т. О ротор любого потенциального поля будет = 0.

,если ротор поля = 0, то поле потенциальное.

* * *

Формулы

, так как это равенство должно выполняться для любых поверхностей S, то из равенства интегралов, следует равенство подынтегральных выражений

Формула