§ 1.5 Электрическое поле диэлектрика

Рассмотрим систему зарядов , которая отличается оси O в небольшой области пространства.

Поместим в эту область начало системы отсчёта и определим потенциал в точке.

* * *

a>>x

* * *

Так как R₀>>R, то подынтегральную функцию мы можем переставить в виде степенного ряда.

Т.о. первый член ряда определяет потенциал по форме точечного заряда. Второй член ряда на много меньше 1го и его вклад будет несущественным, за исключением того случая, когда общий заряд системы q=0, и тогда потенциал будет определяться 2-ым членом ряда, который называется-дипольный момент.

Пример: Определим дипольный момент заряда

Диэлектриком называют тела, заряды которых связаны между собой в неразрывные цепи

Рассмотрим неполимерный диэлектрик. В таком диэлектрике отрицательный заряд атома расположен сферически, симметрично относительно ……………………… В отсутствии внешних полей диэлектрик дипольный момент такого атома равен 0, так как

Если диэлектрик поместить в электрическое поле, то симметрическа картина нарушиться.

В этом случаи у атома появляется дипольный момент , который совпадает с направление вектора и диэлектрик становиться поляризованным.

Полярные диэлектрики

Отрицательные и положительные заряды атома располагаются несимметрично и каждый атом обладает дипольным моментом. Но в отсутствии внешнего поля разряд атомов расспологаеться хаотически и

Если поместить диэлектрик во внешние электрическое поле, то дипольный моменты орентир. Вдоль поля и диэлектрик становиться поляризованным. Для характеристики полеризированного диэлектрика вводят вектор «поляризированность» , который равен суммарному дипольному моменту единиц объёма проводника.

Для определения этого вектора разобьём весь диэлектрик на вdv. Определим суммарный дипольный момент в каждом из этих объёмов, тогда вектор поляризизированности

Процесс возникновения дипольного момента у диэлектрика называется померид

Рассмотри плоскую поверхность ds внутри диэлектрика. Поместим …… в электрическое поле и определим какой положительный заряд был перенесён через эту поверхность приполяризации диэлектрика

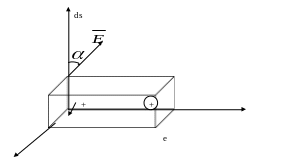
При померизации диэлектрика через поверхность ds пройдут заряды только тех диполей, которые до поляризации находил внутри объёма параллельно объём, которых ds*de cos

Если в единицу объема диэлектрика было к диполей, а заряд каждого диполя q, то через поверхность ds будет перенесён заряд cos =

Так как вектор поляризациовонность то заряд, поляризации будет перенесён через ds

Рассмотрим объём V внутри диэлектрика, который ограниченно замкнут поверхностью S. Определённый заряд, который есть внутри объёма М при потери диэлектрика.

Для этого разобьём по S на dS/ Вычислим заряд перенесённый через каждый участок по формуле , и затем сложим тогда внутри объёма V ост. Заряд Ур. Знака

- Этот заряд называется поляризованным. Его можно за……

- плотность поляризованных зарядов

Так как это рав выю для любого V, то

Пусть в диэлектрике находиться другой заряд(сторонний) кроме зарядов самого диэлектрика

Пусть пл. стор. Зряда –q₀ тогда

- вектор электрического смещения или вектор электрического индукции

Мы будем рассматривать только такие диэлектрики для которых вектор пропорционален вектор

H- диэлектрическая восприимчивость

; диэлектрическая проницаемость

Вычислим поток через произвольную замкнутую поверхность

q₀- сумма всех сторон зарядов, которые находиться внутри поверхности

Энергетическая система зарядов определённых по форме

(§1.4)

Если заряды находиться в диэлектрике то :