11.4. Классификация средств измерений j

Средства измерения, используемые в различных областях науки и техники, чрезвычайно многообразии. Однако для этого множества можно выделить некоторые общие признаки, присущие всем СИ независимо от области применения. Эти признаки положены в основу различных классификаций СИ, которые рассмотрены далее.

По роли, выполняемой в системе обеспечения единещ ва измерений, СИ делятся на:

• метрологические, предназначенные для метрологических целей — воспроизведения единицы и (или) хранения или передачи размера единицы;

• рабочие, применяемые для измерений, не связанных с передачей размера единиц.

По уровню автоматизации все СИ делятся на три группы:

• неавтоматические;

• автоматизированные, производящие в автоматическом режиме одну или часть измерительной операции;

• автоматические, производящие без непосредственного участия человека измерения и все операции связанные с обработкой их результатов (регистрацией), передачей данных или выработкой управляющих сигналов.

По уровню стандартизации средства измерений подразделяются на:

• стандартизованные, изготовленные в соответствии с требованиями государственного или отраслевого стандарта;

• нестандартизованные (уникальные), предназначенные для решения специальной измерительной задачи, в стандартизации требований к которым нет необходимости.

По отношению к измеряемой физической величине средства измерений делятся на:

• основные — это СИ той физической величины, значение которой необходимо получить в соответствии измерительной задачей;

• вспомогательные — это СИ той физической величины, влияние которой на основное средство измерений или объект измерения необходимо учесть для получения результатов измерения требуемой точности.

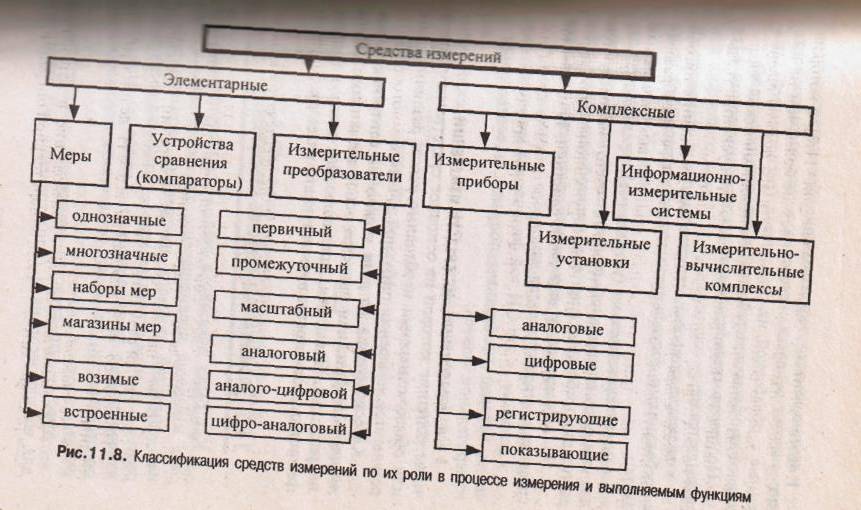
Классификация по роли в процессе измерения и выполняемым функциям является основной и представлена на рис. 11.8. Элементы, составляющие данную классификацию, рассмотрены в последующих разделах.

11.5. Элементарные средства измерений

Как было показано в разд. 11.1, элементарные средства измерений предназначены для реализации отдельных операций прямого измерения, рассмотренных разд. 2.2. К ним относятся меры, устройства сравнений измерительные преобразователи. Каждое из них, взятое по отдельности, не может осуществить операцию измерения.

Мера — это средство измерений, предназначь для воспроизведения и (или) хранения ФВ одного или нескольких размеров, значения которых выражены в установленных единицах и известны с необходимой точностью.

Операцию воспроизведения величины заданного размера можно формально представить как преобразованиe цифрового кода N в заданную физическую величину Х_м, основанное на единице данной физической величины [Q]. Поэтому уравнение преобразования меры запишется в виде

Х_м = N [Q].

Выходом меры является квантованная аналоговая величина Х_м заданного размера, а входом следует считать числовое значение величины N (рис. 11.9).

Меры подразделяют на следующие типы:

• однозначные, воспроизводящие физическую величину одного размера;

• многозначные, воспроизводящие ФВ разных размеров.

Кроме этого, различают наборы мер, магазины мер, щечные, встроенные и ввозимые меры.

Степень совершенства меры определяется постоянством размера каждой ступени квантования [Q] и степенью многозначности, т.е. числом N

воспроизводимых известных значений ее выходной величины. С наиболее высокой точностью посредством мер воспроизводятся основные физические величины: длина, масса, частота, напряжение и ток.

Устройство сравнения —- это техническое средство или специально создаваемая среда, посредством которых возможно выполнять сравнения друг с другом однородных величин или показания измерительных при боров. Примерами могут служить: рычажные весы, на одну чашку которых устанавливается образцовая гиря, а на другую — поверяемая; градуировочная жидкость для сличения показаний образцового и рабочего ареометров; тепловое поле, создаваемое термостатом для сравнения показаний термометров. Во многих относительных простых СИ роль устройства сравнения выполняет зрение человека, например при сравнении отклонения указателя прибора и числа делений, нанесенных на его шкале.

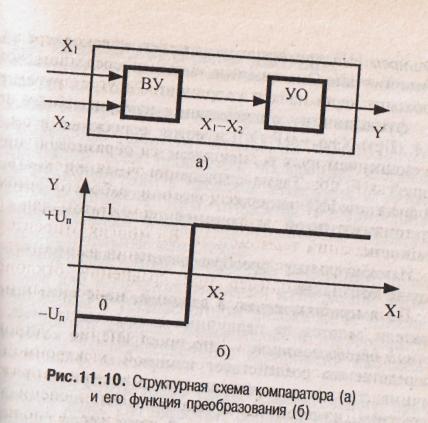
Особенно широкое распространение устройства сравнения получили в современной электронной технике, где они используются для сравнения напряжения и токов. Для этой цели был разработан специальный тип интегральных микросхем. Сравнение, выполняемое компаратором, может быть одно- и разновременные. Первое из них используется гораздо чаще. В электронных компараторах оно реализуется (рис.11.10) путем последовательного соединения вычитающего устройства (ВУ), формирующего разность входных сигнале (Х,-Х₂), и усилителя переменного напряжения с большим коэффициентом усиления (усилителя-ограничителя УО), выполняющего функции индикатора знака разности. Выходной сигнал УО равен его положительному напряжению питания (принимаемого за логическую единицу), если разность (Х,—Х₂) > 0, и отрицательному (принимаемому за логический нуль) — если (X,—Х₂) <0

Функция преобразования идеального компаратора показанная на рис. 11.10, б, описывается уравнением J

Степень совершенства компаратора определяется минимально возможным порогом чувствительности Δ_п, а так же его быстродействием — временем переключения из одного состояния в другое. У идеального компаратора порог Δ_п и время переключения равны нулю. В реальном компараторе наличие порога приводит к возникновению аддитиной погрешности.

Измерительный преобразователь (ИП) предназначен для исполнения одного измерительного преобразования. Его протекает в условиях, когда помимо основного сигнала X, связанного с измеряемой величиной, на него воздействуют множество других сигналов Z_i, pacсматриваемых в данном случае как помехи. Важнейшей характеристикой ИП является функция (уравнение) преобразования которая описывает статические свойства преобразователя и в общем случае записывается в виде Y=F(X, Z_i).

В подавляющем большинстве случаев стремятся иметь линейную функцию преобразования. Функция Y (X) идеального ИП при отсутствии помех описывается уравнением Y = кХ. Она линейна, безынерционна, стабильна и проходит через начало координат. Реальная передаточная функция в статическом режиме имеет вид Y = k (1+γ) X+Δ₀+Δ[F (X)] и может отличаться от идеальной смещением нуля Δ₀ наклоном γ и нелинейной составляющей Δ[F(X)]. Такие отклонения реальной передаточной функции ИП приводят к возникновению аддитивной, мультипликативной и нелинейной составляющих погрешности.

Измерительные преобразователи классифицируются по ряду признаков.

По местоположению в измерительной цепи преобразователи делятся на первичные и промежуточные. Первичный преобразователь — это такой ИП, на который непосредственно воздействует измеряемая физическая величина, т.е. он является первым в измерительной цени средством измерений. Промежуточные преобразователи располагаются в измерительной цепи после первичного Зачастую конструктивно обособленные первичные измерительные преобразователи называют датчиками.

По характеру преобразования входной величины ИП делятся на линейные и нелинейные. Линейный преобразователь — это ИП, имеющий линейную связь мой входной и выходной величинами. Их важной разновидностью является масштабный ИП, предназначенный для изменения размера величины или измерительного сигнала в заданное число раз. У нелинейных ИП связь между входной и выходными величинами нелинейная.

По виду входных и выходных величин ИП делятся :

• аналоговые, преобразующие одну аналоговую величину в другую аналоговую величину;

• аналого-цифровые (АЦП), предназначенные преобразования аналогового измерительного сигнала в цифровой код;

• цифроаналоговые (ЦАП), предназначенные для преобразования цифрового кода в аналоговую величину.