11.3. Динамические характеристики и параметры средств измерений

В статических режимах выходной сигнал СИ в точности соответствует входному (при отсутствии статических погрешностей) и, следовательно, коэффициент преобразования К равен номинальному коэффициенту К_ово всем диапазоне изменения входной величины X(t) Уравнение преобразования имеет вид

Y(t) = K₀X(t) (11.2)

и соответствует идеальному безынерционному линейному преобразованию. Реальные СИ обладают инерционными (динамическими) свойствами, обусловленны­ми особенностями используемых элементов. Это приводит к более сложной зависимости между входным и выходным сигналами. Свойства СИ в динамических режимах, т.е. когда время изменения измеряемой величины сравнимо со временем измерения, описываются совокупностью так называемых динамических характеристик.

Основной их них является полная динамическая характеристика, полностью описывающая принятую математическую модель динамических свойств СИ. В качестве нее используют: дифференциальные уравнения; переходную, импульсную переходную, амплитудно-фазовою амплитудно-частотную характеристики; совокупность амплитудно-частотной и фазочастотной характеристик передаточную функцию.

Дифференциальное уравнение наиболее полно описывает динамические свойства СИ. Его решение Y(t) описывает выходной сигнал средства измерений при входном сигнале X(t). Порядок дифференциального уравнения бывает довольно высоким, по крайней мере выше второго. Его решение весьма затруднено. Дифференциальные уравнения высокого порядка могут быть представлены системой дифференциальных уравнений первого и второго порядков. Это, по существу, означает представление сложного в динамическом смысле СИ совокупностью более простых, хорошо изученных динамических элементов (нулевого, первого и второго порядков).

Элемент нулевого порядка описывается уравнением (11.2), динамический элемент первого порядка — уравнением

+Y(t) = K₀X(t), (11.3)

где Т - постоянная времени. Вместо нее применяют и величину ω_гр= 1 /Т, называемую граничной частотой.

Динамический элемент второго порядка описывается уравнением

+Y(t)= K₀X(t), (11.4)

где ω₀— частота собственных колебаний; β — коэффициент демпфирования, или степень успокоения.

Переходная характеристика h(t) — это временная характеристика СИ, полученная в результате подачи на его вход сигнала в виде единичной функции заданной амплитуды X(t) = X_ml(t). Она описывает инерционность СИ, обуславливающую запаздывание и искажение выходного сигнала относительно входного. Переходую характеристику находят либо опытным путем, либо решая соответствующее дифференциальное уравнение при Х(t) = Х_m1(t).

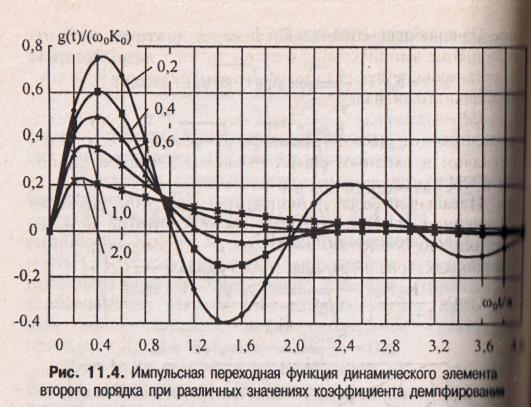
Импульсная переходная характеристика g(t) — это |временная характеристика СИ, полученная в результате приложения к его входу сигнала в виде дельта-функции. Переходная и импульсная характеристики связаны между собой;

h(t) =

Как и дифференциальное уравнение, эти характеристики в полной мере определяют динамические свойства СИ. Выходной сигнал при известном входном X(t) определяют с помощью интеграла Дюамеля:

или

Переходная и импульсная характеристики элементов первого порядка имеют вид:

h(t) = X_mK₀(l-e^-1/^T), g(t)=

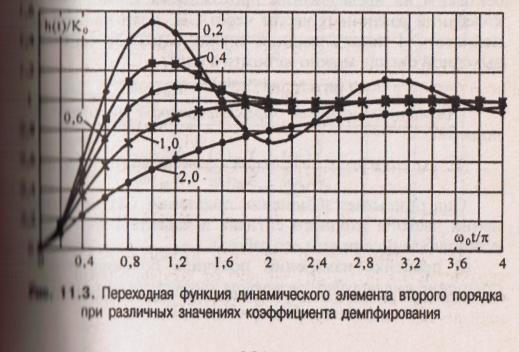
Для динамического элемента второго порядки вид характеристик h(t) и g(t) зависит от коэффициента демпфирования (рис. 11.3 и 11.4). Имеют место три режима (считается, что Х_т = 1):

1) колебательный при

;

2) критический при β = 1

; ;

3) апериодический при р > 1

Критический режим является граничным между колебательным и апериодическим. Он характерен тем, что в таком режиме переходный процесс наиболее быстро стремится к установившемуся значению.

К частотным характеристикам относятся амплитудно-фазовая G(jω), амплитудно-частотная А(ω) и фазочастотная φ(ω) характеристики. Частотные методы анализа основаны на исследовании прохождения гармонических колебаний различных частот через СИ. Если на выход линейного СИ подать входной сигнал X(jω)=X_m (ω)e^{j(ωt+φ(ω))}=Y_m (ω)e^jωt выходной сигнал можно записать в виде

Y(jω) = Y_mе^{j(ωt+φ(ω))} = Y_m(ω)е^jωt.

Амплитудно-фазовой характеристикой называют отношение

Она описывает изменение показаний СИ при изменении частоты входного сигнала и характеризует только установившийся режим его работы.

В практике измерений получила большое распространение амплитудно-частотная характеристика (ЛЧХ)

A(ω) = |G(jω)|=Y_m(ω)/X_m(_ω),

Представляющая собой зависящее от круговой частоты отношение

мплитуды выходного сигнала линейного СИ установившемся режиме к амплитуде входного синусоидального сигнала.

Фазочастотная характеристика (ФЧХ) φ(ω) — это зависящая от частоты разность фаз между выходным сигналом и входным синусоидальным сигналом линейного СИ в установившемся режиме.

Идеальный безынерционный элемент, описываемый уравнением (11.2), имеет следующие частотные характеристики: G(jω) = К₀, φ(ω) = 0, Для элемента первого порядка (рис. 11.5), задаваемого уравнением (11.3),

;

Динамический элемент второго порядка, описываемый уравнением (11.4), имеет следующие частотные характеристики:

для него вид частотных характеристик существенно зависит от коэффициента демпфирования β (рис. 11.6). При β = 0,6...0,7 в относительно широком диапазоне частот . Этот режим важен для практических применений таких элементов. При β < 0,6 наблюдаются резонансные явления для частот, близких к ω₀.

Частотные характеристики СИ связаны с другими его динамическими характеристиками следующими соотношениями:

Н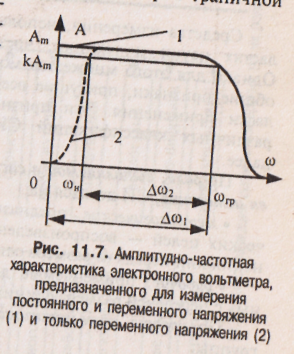 а рис. 11.7 показана типичная для электронного метра и аналогового осциллографа АЧХ. Если метр предназначен для измерения и постоянного и применного напряжения (а осциллограф работает при «открытом» входе), то АЧХ начинается с нулевой частоты (кривая 1) и продолжается до некоторой граничной частоты ω_гр, после которой происходит ее существенный спад. У вольтметров переменного и осциллографов с «закрытым» входом АЧХ при нулевой частоте равна нулю, а затем с ростом частоты достигает (кривая 2) установившегося значения А_m.

Соответствующий граничной частоте ω_гр уровень κА_m (к < 1), до которого спад АЧХ считается допустимым, у различных устройств задается по разному. Характер изменения зависимости А(ω) при частотах, больших граничной ω_гр, также существенно зависит от технической реализации СИ.

Полоса частот Δω₁, (или Δω₂) (см. рис. 11.7), в которой АЧХ средства измерений изменяется не более чем на наперед заданную величину, называется его полосой пропускания. Она является важной частной динамической характеристикой СИ. Часто вместо полосы пропускания указывают начальную ω_н и граничную ω_гр частоты.

Передаточная функция G (р) — это отношение преобразования Лапласа выходного сигнала СИ к преобразованию Лапласа входного сигнала при нулевых начальных условиях.

Кроме полных характеристик часто используются частные, представляющие собой функционал или параметр полной динамической характеристики. К ним относятся: время реакции, неравномерность АЧХ, время нарастания переходной характеристики и ряд других.