8.2. Однократные измерения

Однократные прямые измерения являются самы­ми массовыми и проводятся, если при измерении происходит разрушение объекта измерения, отсутствует возможность повторных измерений, имеет место и комическая целесообразность. Они возможны лишь при определенных ситуациях, а именно, когда:

• объем априорной информации об объекте из­мерений должен быть таким, чтобы его модель и определение измеряемой величины не вызывали сомне­ний;

• изучен метод измерения, его погрешности либо заранее устранены, либо оценены;

• средства измерений исправны, а их метрологические характеристики соответствуют установленным нормам.

За результат прямого однократного измерения принимается полученная величина. До измерения должна быть проведена априорная оценка составляющих погрешности с использованием всех доступных данных. При определении доверительных границ погрешности результата измерений доверительная вероятность принимается, как правило, равной 0,95.

Методика обработки результатов прямых однократных измерений приведена в рекомендациях МИ 1552-86 «ГСИ. Измерения прямые однократные. Оценивание погрешностей результатов измерений».

Данная методика применима при выполнении сле­дующих условий: составляющие погрешности извест­ны, случайные составляющие распределены по нор­мальному закону, а неисключенные систематические, заданные своими границами θ_i, - равномерно.

Составляющими погрешности прямых однократных измерений являются:

• погрешности СИ, рассчитываемые по их метрологическим характеристикам;

• погрешность используемого метода измерений, определяемая на основе анализа в каждом конкретном случае;

• личная погрешность, вносимая конкретным оператором.

Если последние две составляющие не превышают 15% погрешности СИ, то за погрешность результата однократного измерения принимают погрешность используемого СИ. Данная ситуация весьма часто имеет место на практике.

Названные составляющие могут состоять из неисключенных систематических и случайных погреш­ностей. При наличии нескольких систематических погрешностей, заданных своими границами ±θ_i либо доверительными границами ±θ_i(Р), доверительная граница результата измерения соответственно может быть рассчитана по формуле

или

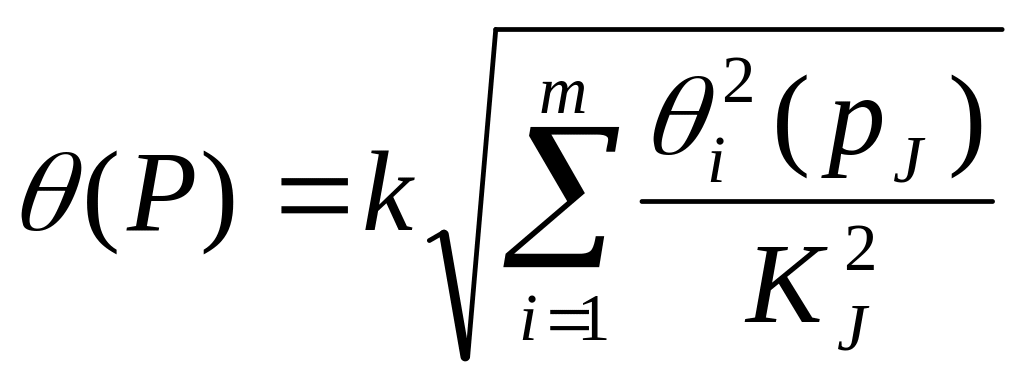
где Ө_i(P_j) —доверительная граница i-й неисключенной систематической погрешности, соответствующая доверительной вероятности Р_j k_j —коэффициент, зависящий от P_j и определяемый так же, как и коэффициент k; k = k (m, P) — коэффициент, равный 0,95 при Р = 0,9 и 1,1 при Р = 0,95. При других доверительных вероятностях он определяется в соответствии с ГОСТ 8.207-76.

Случайные составляющие погрешности результа­та измерений выражаются либо оценками своих СКО S_хi либо доверительными границами ±ε_i(P). В первом случае доверительная граница случайной составляю­щей погрешности результата прямого однократного измерения определяется через его СКО S_x:

ε(P) = z_PS(x) = Z_p ,

где Z_p -точка нормированной функции Лапласа, от­мечающей вероятности Р. При Р=0,95 Z_P= 2. Если СКО S_xi определены экспериментально при неболь­шом числе измерений (n < 30), то в данной формуле вместо коэффициента Z_P следует использовать коэф­фициент Стьюдента, соответствующий числу степени свободы i-й составляющей, оценка которой произведена при наименьшем числе измерений.

В случае, когда случайные погрешности представлены доверительными границами ±ε_i (Р_i), соответствующими разным доверительным вероятностям Р_i

Таблица 8.2

Погрешность результата прямых однократных измерений ∆(Р)

Значение θ/S(х)	Погрешность результат измерения ∆(Р)
θ/Sk<0,8	ε(Р)
0,8≤θ/Sk≤8	kр[ε(Р)+θ(Р)]
θ/Sk>8	θ(Р)

Найденные значения θ и ε(Р) используются для оценки погрешности результата прямых однократных измерений. В зависимости от соотношения θ и S_k суммарная погрешность определяется по одной из формул, приведены в табл. 8.2.

Коэффициент к_Р определяется из табл. 8.3.

Таблица 8.3

Зависимость k_р[θ/S_х] при доверительной вероятности 0,95

θ/Sk	0,8	1	2	3	4	5	6	7	8
K0,95	0,76	0,74	0,71	0,73	0,76	0,78	0,79	0,80	0,81

Результат прямых однократных измерений дол­жен записываться в соответствии с рекомендациями МИ 1317-86 в виде х ± ∆(Р) при доверительной вероятности Р = Р_д.

Выше были рассмотрены прямые однократные измерения с точным оцениванием погрешностей, наиболее детально они проанализированы в [3]. В практике также имеют место прямые однократные измерения с приближенным оцениванием погрешности. Для них характерно оценивание погрешности полученного результата на основе метрологических характеристик, приведенных в документации на используемые средства измерений. Поскольку эти характеристики относятся к любым экземплярам данного типа СИ, то у конкретного используемого средства действительные метрологические характеристики могут отличаться от нормированных.

Прямые однократные измерения с приближенным оцениванием погрешностей правомочны, если доказана возможность пренебрежения случайной составляющей погрешности измерения, т.е. можно обоснованно считать, что ее среднее квадратическое отклонение S_x меньше 1/8 суммарной границы неисключенных систематических составляющих погреш­ности результата измерения.

В простейшем случае, когда влияющие величины соответствуют нормальным условиям, погрешность результата прямого однократного измерения равна пределу основной погрешности средства измерения ∆_си, определяемой по документации. Результат изме­рения запишется в виде ∆ = ±∆_СИ. Доверительная ве­роятность не указывается, но, как правило, подразу­мевается, что она равна 0,95. При проведении изме­рений в условиях, отличных от нормальных, необходимо определять и учитывать пределы допол­нительных погрешностей. Возможная методика сум­мирования основных и дополнительных погрешностей однократных измерений приведена в [3].