Значения точечных оценок распределения Стьюдента при различных степенях свободы

Число степеней свободы k	Эксцесс ε	Контрэксцесс χ
4	∞	0
5	9	0,333
6	6	0,408
10	4	0,500
∞	3	0,577

Разновидностью распределения Стьюдента является распределение Коши. Оно важно тем, что ему подчиняется распределение отношения двух нормально распределен­ных центрированных случайных величин. Распределение Коши — это предельное распределение семейства зако­нов Стьюдента с минимально возможным числом степе­ней свободы к = 1 (см. рис. 6.6):

В общем виде (не нормированном и не центрированном) распределение Коши имеет вид

где А, Х_ц— параметры распределения.

Свойства распределения Коши резко отличаются от свойств экспоненциальных распределений, а именно:

• дисперсия и С КО не существуют, так как определяющий их интеграл расходится; они будут бесконечно увеличиваться при росте числа экспериментальных данных. Оценка ширины распределения может быть произведена только на основе теории информации;

• оценка центра в виде среднего арифметического для распределения Коши не правомочна, так как ее рассеяние равно бесконечности;

• математическое ожидание не существует;

• для определения Х_ц необходимо использовать медиану;

• эксцесс равен бесконечности, а контрэксцесс рати нулю.

К двухмодальным распределениям относятся:

• Дискретное двузначное распределение, в котором с равными вероятностями встречаются только два значения случайной величины. В центрированном виде (рис. 6.7) оно описывается формулой

|р(х) = 0,5δ(х + А) + 0,5δ(х-А),

где δ(х) — дельта-функция Дирака; +А — возможные значения случайной величины

Для дискретного двузначного распределения СКО равно значению параметра А, ε= 1, χ ⁼ 1.

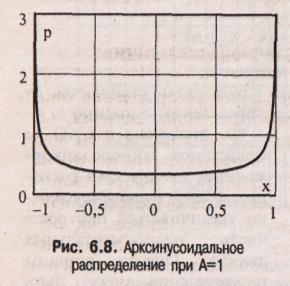
• Арксинусоидальное распределение (рис. 6.8), описываемое выражением

где А — параметр распределения.

Его СКО равно , ε=1,5,χ = 0,816.

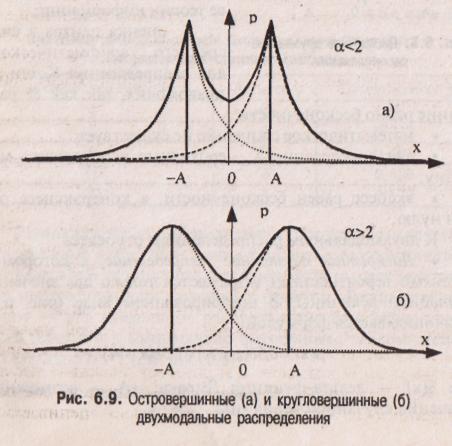
• Остро- и кругло-вершинные двухмодапьные распределения, получаемые как композиция дискретного двузначного и экспоненциального распределений с различными значениями коэффициента а (рис. 6.9). При а < 2 имеем островершинные, при а > 2 — кругловершинные распределения.

6.4 Точечные оценки законов распределения

Рассмотренные выше функции распределения описывают поведение непрерывных случайных величин, т.е. величин, возможные значения которых неотделимы друг от друга и непрерывно заполняют некоторый конечный или бесконечный интервал. На практике все результаты измерений и случайные погрешности являются величинами дискретными, т.е. величинами х„ возможные значения которых отделимы друг от друга и поддаются счету. При использовании дискретных случайных величин возникает задача нахождения точечных оценок параметров их функций распределения на основании выборок— ряда значений х_i( принимаемых случайной величиной х в n независимых опытах. Используемая выборка должна быть репрезентативной (представительной), т.е. должна достаточно хорошо представлять пропорции генеральной совокупности.

Оценка параметра называется точечной, если она выражается одним числом. Задача нахождения точечных оценок — частный случай статистической задачи нахождения оценок параметров функции распределения случайной величины на основании выборки. В отличие от самих параметров их точечные оценки являются случайными величинами, причем их значения зависят от объема экспериментальных данных, а закон распределения — ОТ законов распределения самих случайных величин.

Точечные оценки могут быть состоятельными, несмещенными и эффективными. Состоятельной называется оценка, которая при увеличении объема выборки стремится по вероятности к истинному значению числовой характеристики. Несмещенной называется оценка, мин математическое ожидание которой равно оцениваемой числовой характеристике. Наиболее эффективной считают ту из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию.

Точечной оценкой МО результата измерений является среднее арифметическое значение измеряемой величины

(6.6)

При любом законе распределения оно является состоятельной и несмещенной оценкой, а также наиболее эффективной по критерию наименьших квадратов.

Точечная оценка дисперсии, определяемая по формуле

(6.7)

является несмещенной и состоятельной.

Оценка среднего квадратического отклонения

(6.8)

Полученные оценки МО и СКО являются случайными величинами. Это проявляется в том, что при повторении несколько раз серий из п наблюдений каждый раз будут получаться различные оценки и . Рассеяние этих оценок целесообразно оценивать СКО S и Sσ. Оценка СКО среднего арифметического значения

(6.9)