Значения параметров экспоненциальных распределений при различных значениях показателя α

Вид распределения	α	ε	χ
Лапласа	1	6	0,408
Гаусса (нормальное)	2	3	0,577
Равномерное	∞	1,8	0,745

А нализ приведенных выражений показывает, что константа α однозначно определяет вид и все параметры распределений. При α<1 распределение имеет очень по­логие спады и по форме близко к распределению Коши. При α = 1 получается распределение Лапласа p(х) = 0,5е^-|х|, при α = 2 — нормальное распределение, или распределение Гаусса. При α > 2 распределения, описываемые формулой (6.3), близки по свойствам к трапецеидальным. При очень больших значениях α формула (6.3) описывает практически равномерное распределение. В табл. 6.1 приведены параметры некоторых из экспоненциальных распределений.

Вид экспоненциальных распределений при различ­ных значениях показателя α приведен на рис. 6.5.

Наибольшее распространение получило нормальное распределение, называемое часто распределением Гаусса:

, (6.4)

где σ—параметр рассеивания распределения, равный СКО; Х_ц — центр распределения, равный МО.

Вид нор­мального распределения показан на рис. 6.2.

Широкое использование нормального распределе­ния на практике объясняется центральной предельной теоремой теории вероятностей [24, 25], утверждающей, что распределение случайных погрешностей будет близ­ко к нормальному всякий раз, когда результаты наблю­дений формируются под действием большого числа не­зависимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.

При введении новой переменной из формулы (6.4) получается нормированное нормальное распределение, интегральная и дифференциальная функции которого соответственно равны:

Нормирование приводит к переносу начала коорди­нат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функций нормированного нормального распределения сведены в таблицы, которые можно найти в литературе по теории вероятностей [24, 25].

Определенный интеграл с переменным верхним пре­делом

(6.5)

называют функцией Лапласа. Для нее справедливы сле­дующие равенства: Ф(-∞) = -0,5; Ф(0) = 0; Ф(+∞) = 0 5; Ф(t) = -Ф(t).

Функция Лапласа используется для определения значений интегральных функций нормальных распреде­лений. Функция F(t) связана с функцией Лапласа фор­мулой F(t) = 0,5 + Ф(t). Поскольку интеграл в (6.5) не выражается через элементарные функции, то значения функции Лапласа для различных t сведены в таблицу (см. приложение 2, табл. П2.1).

Семейство распределений Стъюдента описывает плотность распределения вероятности значений средне­го арифметического, вычисленного по выборке из п слу­чайных отсчетов нормально распределенной генераль­ной совокупности. Распределения Стьюдента нашли широкое применение при статистической обработке ре­зультатов многократных измерений. Их вид зависит от числа отсчетов n, по которым находится среднее арифме­тическое значение, поэтому и говорят о семействе зако­нов.

В центрированном и нормированном виде они опи­сываются формулой

г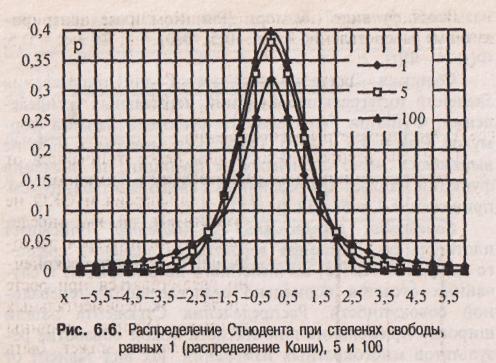 де k — число степеней свободы, зависящее от числа п усредняющих отсчетов: k = n - 1. Вид распределения Стью­дента для различных значений k показан на рис. 6.6. При увеличении k распределение Стьюдента переходит в рас­пределение Гаусса.

Для нормированных распределений Стьюдента с к > 4 справедливы следующие соотношения:

, ; ;

Значения некоторых параметров для различных сте­пеней свободы приведены в табл. 6.2.

Таблица 6.2