6.2.3. Моменты распределений

Все моменты представляют собой некоторые сред­ние значения, причем если усредняются величины, от­считываемые от начала координат, то моменты называют начальными, а если — от центра распределения, то цен­тральными. Начальные и центральные моменты r-го по­рядка определяются соответственно по формулам

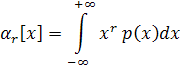
Нулевой начальный момент равен единице. Он ис­пользуется для задания условия нормирования плотно­сти распределения:

С помощью начального момента нулевого порядка вводится понятие медианы распределения. Первый на­чальный момент является МО случайной величины.

Важное значение имеет второй центральный момент

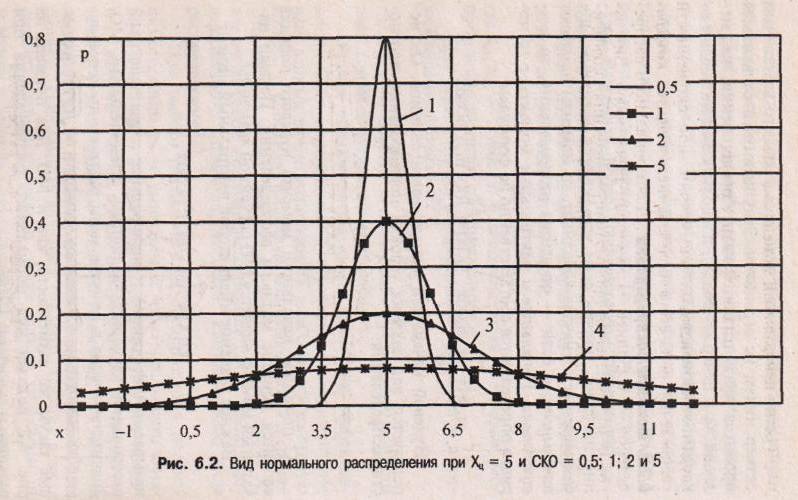
называемый дисперсией и являющийся характеристикой рассеивания случайной величины относительного МО. Значительно чаще в качестве меры рассеивания использу­ется среднее квадратическое отклонение , имею­щее такую же размерность, как и МО. Для примера на рис. 6.2 показан вид нормального распределения при различных значениях СКО.

Третий центральный момент

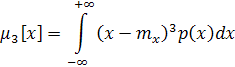
служит характеристикой асимметрии, или скошенности распределения. С его использованием вводится коэффи­циент асимметрии ν = μ₃[Х]/σ³. Для нормального распре­деления коэффициент асимметрии равен нулю. Вид за­конов распределения при различных значениях коэффи­циента асимметрии приведен на рис. 6.3, а.

Ч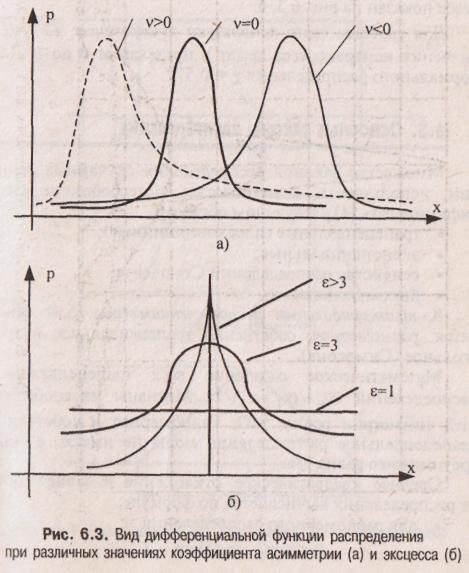 етвертый центральный момент

служит для характеристики плоско- или островершинно­сти распределения. Эти свойства описываются с помо­щью эксцесса

ε = μ₄ [Х]/σ⁴ (6.3)

Его значения лежат в диапазоне от 1 до да. Для нор­мального распределения £ = 3. Вид дифференциальной функции распределения при различных значениях экс­цесса показан на рис. 6.3, б.

Для удобства часто используют контрэксцесс Значения контрэксцесса лежат в пределах от 0 до 1. Для нормального распределения % = 0,577.

6.3. Основные законы распределения

Множество законов распределения случайных вели­чин, используемых в метрологии, целесообразно клас­сифицировать [4] следующим образом:

• трапецеидальные (плосковершинные);

• экспоненциальные;

• семейство распределений Стьюдента;

• двухмодальные.

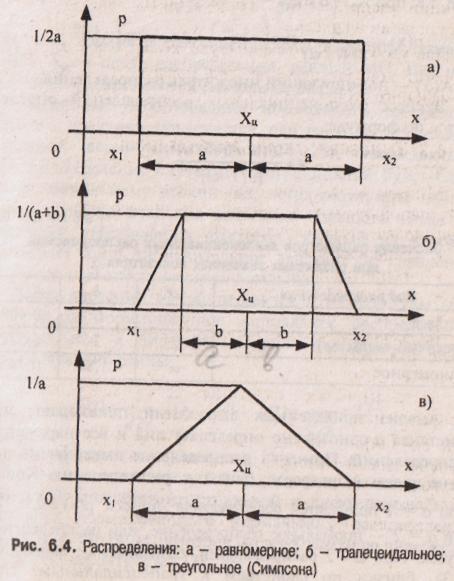
К трапецеидальным распределениям (рис. 6.4) отно­сятся: равномерное, собственно трапецеидальное и тре­угольное (Симпсона).

Математическое ожидание всех трапецеидальных распределений

Х_ц=(х₁+х₂)/2. Медианы из соображе­ний симметрии равны МО. Равномерное и собственно трапецеидальное распределения моды не имеют, а мода треугольного равна 1/а.

Среднее квадратическое отклонение в зависимости от распределения вычисляется по формуле:

• для равномерного распределения

• для трапецеидального —

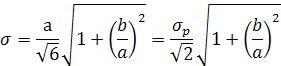
• для треугольного распределения

Коэффициент асимметрии всех трапецеидальных распределений равен нулю.

Экспоненциальные распределения описываются фор­мулой [4]

(6.5)

где ; σ - СКО; α - некоторая харак­терная для данного распределения константа; Х_ц — коор­дината центра; Г(х) — гамма-функция. В нормированном виде, т.е. при Х_ц = 0 и αλ = 1,

где А(α) — нормирующий множитель распределения.

Эксцесс экспоненциальных распределений опреде­ляется по формуле:

Таблица 6.1