6. Случайные погрешности

6.1. Вероятностное описание случайных погрешностей

Из теории вероятностей известно, что наиболее уни­версальным способом описания случайных величин яв­ляется отыскание их интегральных или дифференциаль­ных функций распределения. Интегральной функцией распределения F(x) называют функцию, каждое значение которой для каждого х является вероятностью события, заключающегося в том, что случайная величина х_i в i-м опыте принимает значение, меньшее х:

F(x) = Р{x_i<x} = Р{-∞<x_i ≤x}. (6.1)

График интегральной функции распределения пока­зан на рис. 6.1. Она имеет следующие свойства:

• неотрицательная, т. е. F(x) > 0;

• неубывающая, т. е. F(x₂) ≥F(x₁), если х₂ ≥ х₁;

• диапазон ее изменения простирается от 0 до 1, т.е. F(-∞) = 0; F(+∞)=l;

• вероятность нахождения случайной величины х в диапазоне от х₁ до х₂ Р {х₁ < х < х₂} = F(x₂) - F(x₁).

Более наглядным является описание свойств результа­тов измерений и случайных погрешностей с помощью диф­ференциальной функции распределения, иначе называемой плотностью распределения вероятностей р(х) = dF(x)/dx. Она всегда неотрицательна и подчиняется условию нормирова­ния в виде

Учитывая взаимосвязь F(x) и р(х), легко показать, что вероятность попадания случайной величины в за­данный интервал (х,; х₂)

С ледовательно, рассмотренное выше условие нор­мирования означает, что вероятность попадания величины х в интервал [-∞; +∞] равна едини­це, т.е. представ­ляет собой досто­верное событие.

Из последнего уравнения следу­ет, что вероятность попадания случай­ной величины х в заданный интер­вал (х₁; x₂) равна площади, заклю­ченной под кривой р(х) между абсцис­сами х₁ и х₂ (см. рис. 6.1). Поэтому по форме кривой плотности вероят­ности р(х) можно судить о том, какие значения случайной величины х наи­более вероятны, а какие менее.

6.2. Числовые параметры законов распределения

6.2.1. Общие сведения

Как отмечалось выше, функции распределения яв­ляются самым универсальным способом описания поведения результатов измерений и случайных погрешно­стей. Однако для их определения необходимо проведе­ние весьма длительных и кропотливых исследований и вычислений. В большинстве случаев бывает достаточно охарактеризовать случайные величины с помощью огра­ниченного числа специальных параметров, основными из которых являются:

• центр распределения;

• начальные и центральные моменты и производ­ные от них коэффициенты — математическое ожидание (МО), СКО, эксцесс, контрэксцесс и коэффициент асимметрии.

6.2.2. Понятие центра распределения

Координата центра распределения определяет поло­жение случайной величины на числовой оси и может быть найдена несколькими способами. Наиболее фунда­ментальным является отыскивание центра по принципу симметрии, т. е. такой точки Х_м на оси х, слева и справа от которой вероятности появления различных значений случайной величины одинаковы и равны 0,5:

Точку Х_м называют медианой, и 50%-ным кванти­лем. Для его нахождения у распределения случайной ве­личины должен существовать только нулевой начальный момент.

Можно определить центр распределения как центр тяжести распределения, т. е. такой точки X , относительно которой опрокидывающий момент геометрической фигу­ры, огибающей которой является кривая р(х), равен нулю:

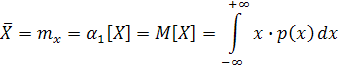
Эта точка называется математическим ожиданием. Сле­дует отметить, что у некоторых распределений, например распределения Коши, не существует МО, так как опре­деляющий его интеграл расходится.

При симметричной кривой р(х) в качестве центра может использоваться абсцисса моды, т.е. максимума распределения Х_m. Однако существуют распределения, у которых нет моды, например равномерное. Распределе­ния с одним максимумом называются одномодальными, с двумя — двухмодальными и т.д. Те из них, у которых в средней части расположен не максимум, а минимум, на­зываются антимодальными.

Для двухмодальных распределений применяется оценка центра в виде центра сгибов:

Х_с=(х_с1+х_с2)/2,

где x_c1, х_с2 — сгибы, т. е. абсциссы точек, в которых рас­пределение достигает своих максимумов.

Для ограниченных распределений применяется оцен­ка в виде центра размаха;

Х_p = (х₁+х₂)/2,

где х₁ х₂ — первый и последний члены вариационного ряда, соответствующего распределению.

Разные оценки центра имеют различную эффектив­ность. При статистической обработке эксперименталь­ных данных важно использовать наиболее эффективную из них, т. е. оценку, имеющую минимальную дисперсию. Это связано с тем, что погрешность в определении Х_ц влечет за собой неправильную оценку СКО, границ до­верительного интервала, эксцесса, контрэксцесса, вида распределения [4].

При выборе оценки центра распределения необхо­димо принимать во внимание ее чувствительность к на­личию промахов в обрабатываемой совокупности исход­ных данных. Оценка в виде центра размаха Х_р исключи­тельно чувствительна к наличию промахов, так как она определяется по наиболее удаленным от центра наблю­дениям, каковыми и являются промахи. Оценка в виде среднего арифметического также слабо защищена от влияния промахов. Оно ослабляется лишь в раз, где n — число наблюдений, в то время как его возможный размер ничем не ограничен. Защищенными от влияния промахов являются лишь квантильные оценки, т.е. ме­диана Х_м и центр сгибов X_c, поскольку они не зависят от координат промахов.