5. Последовательное и параллельное соединение сопротивлений.

П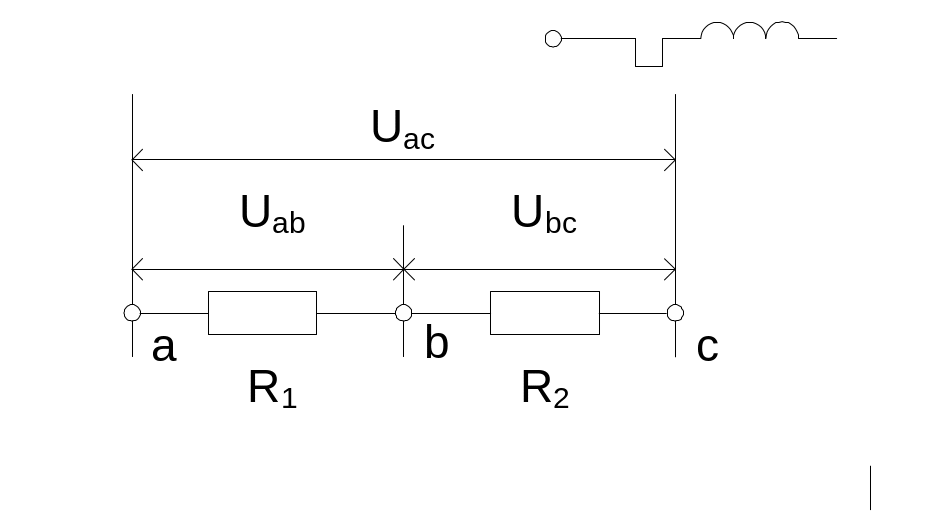 оследовательным называется такое соединение сопротивлений, когда по ним может протекать один и тот же ток:

Здесь, очевидно,

U=U_ab+U_bc=R₁I+R₂I=(R₁+R₂)I.

Обозначим общее сопротивление через R:

R=U/I=R₁+R₂.

Часто, зная величины U, R₁ и R₂, приходится решать вопрос о напряжении на одном из сопротивлений. Например, обозначим

U₂=R₂I.

Так как

I=U/(R₁+R₂).

Напряжение, приложенное к последовательной цепи,делится пропорционально сопротивлениям, включенным в цепь.

Если сопротивлений больше, чем 2, то

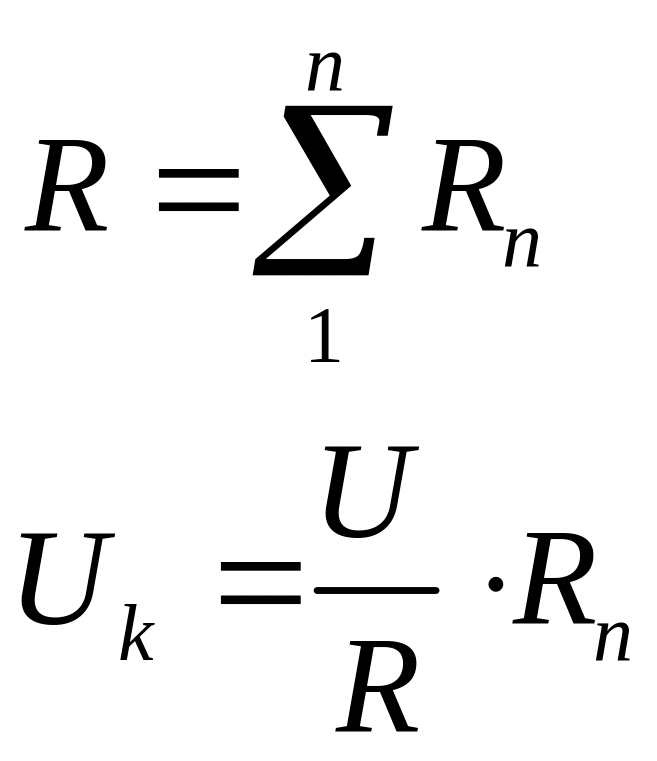
(n-количество сопротивлений).

Теперь найдем общую проводимость последовательной цепи.

Из R=1/G следует, что общую проводимость последовательной цепи можно найти таким образом:

Для n=2

, откуда

Теперь найдем общую проводимость последовательной цепи.

Параллельным называется такое соединение сопротивлений (лучше было бы сказать – резисторов), когда к ним можно приложить лишь одно и тоже направление.

Это значит, что у них взаимно соединены оба полюса:

Здесь:

I=I₁+I₂+…+I_n=G₁U+G₂U+…+G_nU=(G₁+G₂+…+G_n)U.

Обозначив I/U=G, получим, что общая проводимость равна

Найдем ток в k-той ветви, если известен ток I и все проводимости:

I_k=G_kU

U=I/G

отсюда I_k=G_kI/G.

Ток в параллельной цепи делится пропорционально цепи можно найти следующим образом:

откуда

Для двух сопротивлений, включенных параллельно,

Часто приходится определять токи и двух параллельных сопротивлениях, зная величины I, R₁ и R₂:

О чевидно, что здесь RI=R₁I₁= R₂I₂=U. Так как , получаем:

То же самое получим, выразив проводимости в формуле I_k=G_kI/G через сопротивления:

5. Источники тока.

И деальным источником тока мы будем называть такой двухполюсник, через который протекает неизменный ток, независимо от напряжения на его полюсах:

Через источник тока всегда протекает ток I, равный J. Величину J часто называют задающим током источника. Источник тока работает в режиме генератора, если на его зажимах напряжение направлено, как показано на

рисунке выше. Если же действием внешней цепи по лярность напряжения изменить на обратную, этот источник будет работать в режиме потребителя:

Ток здесь течет через источник в том же направлении, в котором действует на него приложенное напряжение.

Сравним идеальный источник тока с идеальным источником напряжения. Для этого изобразим их внешние характеристики на одном чертеже:

Т еперь рассмотрим источник тока, включенный на переменную проводимость G:

Н апряжение U=J/G стремится к бесконечности при G стремящейся к 0; но режим G=0 означает R=1/G и равно бесконечности, т.е. холостой ход источника тока. Значит, для идеального источника тока невозможен холостой ход.

Если для источника напряжения режим отсутствует

нагрузки – это режим холостого хода, то для источника тока – это режим короткого замыкания.

Р еальный источник тока должен обладать некоторой внутренней проводимостью G_b:

Тогда при холостом ходе (внешние зажимы разомкнуты) на его полюсах будет существовать напряжение U_x=J/ G_b.

Нагрузка присоединяется к такому источнику тока:

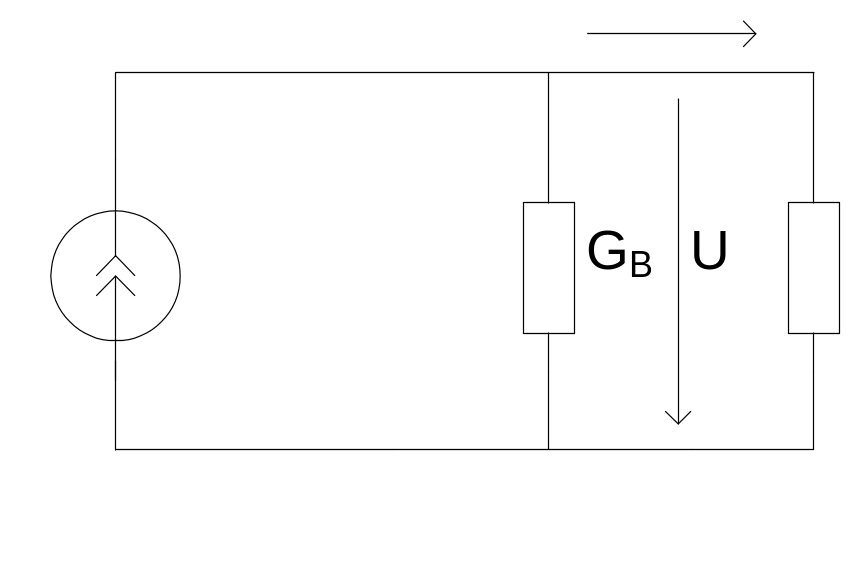
Внешняя характеристика реального источника такова:

П ри коротком замыкании, т.е. когда G равно бесконечности, весь ток J протекает по внешней цепи:

При этом U_x=0.

Нетрудно видеть, внешняя характеристика

источника тока подобна внешней характеристике

источника эдс. Чтобы они совпали, необходимо

сделать:

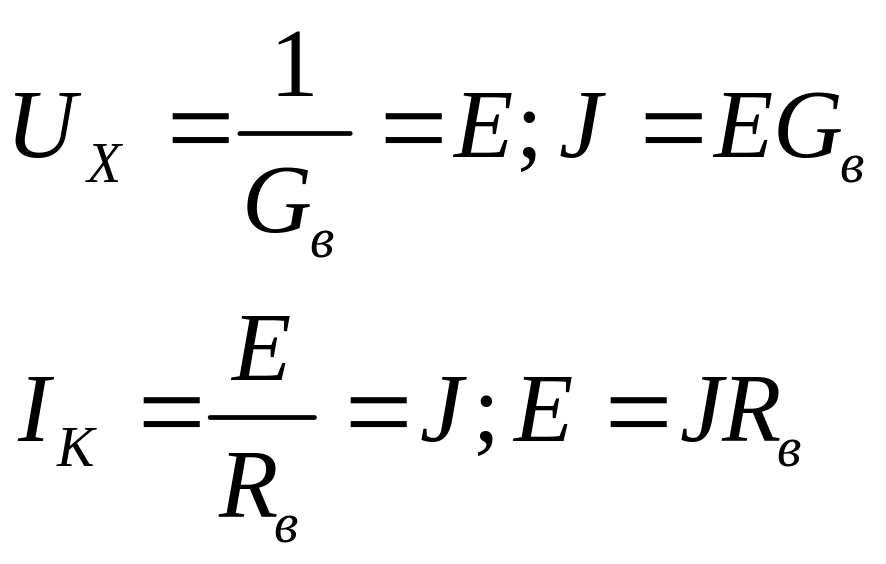
Это есть условия эквивалентности источника эдс и тока. Пусть известны E и R_b источника эдс. Нетрудно видеть, что параметры эквивалентного источника тока равны J=E/ R_b; G_b =1/R_b/

Очевидно, что идеальные источники эдс и тока не могут быть эквивалентными.

Р еальный источник тока приближается по своим свойствам к идеальному, если его внешняя характеристика по своим свойствам к идеальному, если его внешняя характеристика мало отличается от вертикальной прямой:

Это означает, что он должен работать в режиме G_b<<G.

Ток, ответвляющийся в G_b, должен быть значительно меньше тока нагрузки I.

Такой источник может выйти из строя при холостом ходе (U_x слишком велико).

Эквивалентный ему источник эдс обладает очень большим по сравнению с нагрузкой внутренним сопротивлением.

Действительно, при R_b>>R ток в нагрузке I=E/( R_b+R) определяется, главным образом, величиной R_b, т.е. можно изменять сопротивление R в довольно широких пределах, а ток в нем будет изменяться незначительно.

Поэтому вопрос о том, как удобнее представлять реальные источники электрической энергии в виде источников эдс или тока—решается в зависимости от соотношения внутреннего и внешнего сопротивлений.

Если R_b<<R, то это – источник эдс, если же R_b>>R (G_b<<G), то источник тока.